一种改进天鹰优化算法优化负荷峰谷时段划分以及峰谷电价方法

1.本发明属于电力市场领域，具体涉及一种峰谷时段划分和峰谷电价的优化方法。


背景技术：

2.需求侧管理(dsm)是通过价格信号引导电力消费者采取合理的用电结构和方式的一种手段，在一些国家已经取得了一定成果。采用分时电价是dsm的重要途径之一，其中峰谷分时电价是分时电价的最主要组成部分。其最基本思想是体现电能在负荷高峰时作为短缺商品的价值，运用价格杠杆的作用引导终端用户的用电行为，提高电网安全性以及负荷率水平，引导用户根据自身生产方式的可调节性和利益改变用电方式，进而影响系统负荷。峰谷时段的划分和峰谷电价比价关系的确定是制定峰谷分时电价的基础。
3.根据峰谷时段划分的理论，目前已开展的划分方法主要有以下2种：
①
基于供电成本变化分析。该方法结合机组运行状况建立发电成本-负荷函数，利用该函数在负荷点的突变特征来划分峰谷时段区间，该方法较为复杂，在实际中不易实施。
②
基于负荷曲线分布分析。该方法一般采用模糊半梯形隶属度函数法，根据负荷曲线上各点分别处于峰、谷时段的可能性来划分峰谷时段区间，该方法可操作性强，但是根据隶属度函数阈值难以合理界定各时段区间分界时刻点。
4.峰谷电价(time of use price，tou price)是一种基于价格的需求侧管理措施，合理的峰谷电价水平可以达到削峰填谷、实现供电公司和用户双赢的目的。但是，如果峰谷电价比太高将导致用户对电价响应过度，峰谷时段产生了较大的漂移，甚至产生峰谷倒置，调峰失败的同时电网经济利益受损。峰谷电价比太低又会使用户响应不足，无法达到峰谷电价制定的预期效果。所以，有效地测量和量化用户对峰谷分时电价的响应是十分必要的。现有的峰谷电价难以充分挖掘需求响应的效益，峰谷时段划分也不太合理，另一方面，制定峰谷分时电价时也没有充分考虑用户对该政策的满意度，寻找经济效益和用户满意度以及其他系统目标之间的均衡点。


技术实现要素：

5.为解决上述问题，本发明提出一种改进天鹰优化算法优化负荷峰谷时段划分以及峰谷电价方法，利用模糊隶属度函数法和模糊聚类组合方法，根据构造的阈值指标函数λ
tif
和修正方案，解决模糊隶属度函数法难以界定峰、谷区间分解点的问题，同时采用改进的天鹰优化算法优化峰谷电价，建立的目标函数综合考虑了削峰填谷的效果和用户的综合满意度，通过与某地区原峰谷电价方案相比，本发明提出的方法峰谷时段划分更符合负荷曲线特征，优化后的峰谷定价有效减少了最大负荷和负荷峰谷差，改进的天鹰优化算法与传统粒子群算法优化结果进行对比，解决粒子群算法易陷入局部最优，收敛速度慢的缺点。
6.本发明采用以下技术方案：
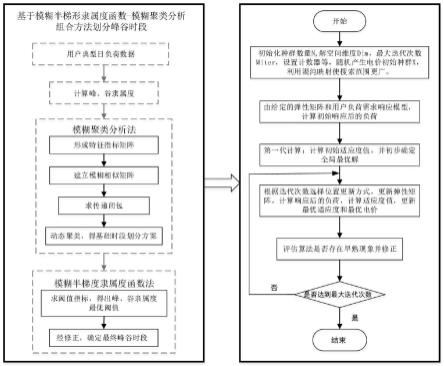
7.一种改进天鹰优化算法优化负荷峰谷时段划分以及峰谷电价方法，包括以下步
骤：
8.步骤一，根据电力系统负荷数据，以1h为单位将一天分为24个时点，组成时间点集合t＝{t1，t2，
…
，t
24
}，各时间点对应的负荷值集合为q＝{q1，q2，
…
，q
24
}，利用模糊半梯形隶属函数法，分别采用偏大型半梯度隶属度函数和偏小型半梯度隶属度函数，初步确定ti时刻的峰、谷隶属度x
i1
和x
i2
；
9.步骤二，采用模糊聚类分析方法，以各时刻的峰、谷隶属度x
i1
和x
i2
做为统计指标，经过标定以及聚类等步骤，得到峰、平、谷时段的聚类集合tf、t
p
和tg；
10.步骤三，运用集合分类思想，基于模糊聚类分析方法得出的基础时段划分结果，计算构造的阈值指标函数λ
tif
，进一步确定偏大型和偏小型半梯形隶属函数的最优阈值λ1和λ2；
11.步骤四，根据偏大型和偏小型半梯形隶属函数的最优阈值λ1和λ2，将其与ti时刻的峰、谷隶属度x
i1
和x
i2
比较得出峰谷时段划分结果，针对隶属度函数阈值难以合理界定各时段区间分界时刻点的问题，参考基础方案和已实施的时段划分方案的特点，经过修正策略得出最终峰谷时段划分方案；
12.步骤五，根据最终峰谷时段划分方案，建立用户弹性响应矩阵，并建立用户负荷的需求响应模型；
13.步骤六，构建用户用电方式满意度和用户电费支出满意度模型，经过线性加权得出用户综合满意度模型，构建以系统谷值负荷最大、负荷峰谷差值最小、用户综合满意度最高为目标函数的峰谷分时电价及负荷优化模型；约束条件分别为电价调整前后总用电负荷需求量不变、峰、谷电价边界约束，用户和供电公司收益约束；利用改进天鹰优化算法获得优化后的分时电价和该分时电价下的需求响应负荷曲线。
14.进一步的，所述步骤一中，ti时刻的峰、谷隶属度x
i1
和x
i2
，由如下方法计算得到：
[0015][0016]
为ti时点的负荷值，a，b分别为各时点对应的负荷中的最小值和最大值。
[0017]
进一步的，在所述步骤二中，采用模糊聚类分析方法包括以下步骤：
[0018]
⑴
以各时点负荷为分类对象，以各时刻的峰、谷隶属度x
i1
和x
i2
做为统计指标，此时：xi＝(x
i1
，x
i2
)，式中：i＝1，2，
…
，24
[0019]
得到特征指标矩阵x为：
[0020][0021]
⑵
将特征指标矩阵x做标准化变换，基于绝对值减数法建立模糊相似矩阵r(r)
24
×
24
；其中r(x
i1
，x
i2
)＝r
ij
，r
ij
由下式计算：
[0022]
[0023]
式中：i，j＝1，2，
…
，24；m＝1，2；σ为适当选取的参数，使得r
ij
∈[0,1]，
[0024]
|x
im-x
jm
|表示xi与xj之间的距离；
[0025]
⑶
对相似矩阵r(r)
24
×
24
求平方，即r
→
r2→…→r2k
，直到第一次出现rk×rk
＝rk，rk即为代求的传递闭包，记t(r)＝(t
ij
)
24
×
24
；
[0026]
⑷
求传递闭包的截矩阵r
δ
，r
δ
＝(δγ
ij
)
24
×
24
，δγ
ij
由下式计算：
[0027][0028]
式中：i，j＝1，2，
…
，24；δ∈[0,1]，令δ从1逐渐减小，按r
δ
进行动态聚类，聚类数取3，即可得到峰、平、谷时段的聚类聚合tf，t
p
和tg。
[0029]
进一步的，在所述步骤三中，运用集合分类思想，根据模糊聚类分析方法所得的峰、平、谷时段的聚类集合tf，t
p
和tg，阈值指标函数λ
tif
由如下方法计算得到：
[0030][0031]
p
fl
、p
pu
、p
pl
和p
gu
分别为tf集合时点对应负荷中最小负荷值、t
p
集合时点对应负荷中最大负荷值、t
p
集合时点对应负荷中最小负荷值和tg集合时点对应负荷中最大负荷值，pi、pj为tf集合时点对应负荷中任意两个不同的负荷值，βi、βj为t
p
集合时点对应负荷中任意两个不同的负荷值，αi、αj为tg集合时点对应负荷中任意两个不同的负荷值；阈值指标函数λ
tif
分子表征相邻集合中样本之间的最小距离，分母表征集合内样本间的最大差距，根据集合分类思想，使不同集合中的样本差异明显化，同一集合内的样本差异模糊化，因此，λ
tif
越大说明峰、平、谷时段划分越好。
[0032]
进一步的，在所述步骤四中，针对隶属度函数阈值难以界定各时段区间分界时刻点问题，作出以下修正方案：
[0033]
①
高峰、平时、低谷3个时段集合内的时间点数量应控制在6～10个；划分方案应符合典型日负荷曲线特征，例如典型的双峰性，上午和下午一般各出现一次用电高峰，低谷通常出现在夜间。具体可通过修正隶属度函数阈值，然后比较阈值指标函数λ
tif
来合理规范峰、平、谷时段集合的大小；
[0034]
②
所划分的时段应具有可行性和实施的便利性，因此高峰、平时、低谷集合中的每个时段不应小于2h；如果出现某个时间点被孤立出来时，要根据模糊聚类分析方法得出的基础方案和孤立点及其相邻点对应负荷值的相对大小进行调整。
[0035]
进一步的，在所述步骤五中，基于最终峰谷时段划分方案，确定用户弹性响应矩阵，并建立的用户负荷的需求响应模型如下：
[0036]
用户弹性响应矩阵m如下：
[0037][0038]
式中，下标f、p、g分别代表峰、平、谷3个时段，对角线上的元素表征自弹性系数，非对角线上的元素表征交叉弹性系数；
[0039]
用户负荷需求响应后的用电量为各时段原用电量与用电量变化的和，模型如下：
[0040][0041]
式中，e
tou
＝[e
f e
p eg]
t
为实施峰谷分时电价后的各时段用电量；e0＝[e
0f e
0p e
0g
]
t
为原各时段用电量；p
0f
、p
0p
、p
0g
分别为实施分时电价前各时段的电价；δpf、δp
p
、δpg分别为实施分时电价前后各时段的电价变化量；在此基础上将峰、平、谷各时段求的总的用电量的变化量，分别以各时段内每小时原用电量对应的比例系数分摊到各个小时，便可得出实施分时电价后各个小时用电量的变化，进而得出实施后的各时点负荷值。
[0042]
进一步的，在所述步骤六中，建立的用户用电方式满意度和用户电费支出满意度模型如下：
[0043]
用电方式满意度μ表示为：
[0044][0045]
其中，表示实行峰谷分时电价后各时间点用电量变化的和，式中，s
tou,t
(pf,p
p
,pg)为实行分时电价后的t时段的用电负荷，pf、p
p
、pg分别为峰、平、谷时段的电价，s
t
(p
t
)表示未实行峰谷分时电价时时段的用电负荷，它是t时段电价p
t
的函数。
[0046]
μ体现了用户用电时间调整后的舒适度，μ∈[0,1]，即用户各时间点用电量未改变时用电方式满意度最高；
[0047]
用电支出满意度表示为：
[0048][0049]
其中，c
tou
为实行峰谷分时电价后用户总的电费支出，c0为实施前用户总的电费支出；
[0050]
用户综合满意度采用用电方式满意度和电费支出满意度的加权平均数，具体模型为：
[0051][0052]
其中，ε1+ε2＝1，ε1和ε2根据用户对用电方式和电费支出的重视程度灵活选取，可根据用户类型参考模糊描述的赋值方法选取；
[0053]
根据步骤六中以系统谷值负荷最大、负荷峰谷差值最小、用户综合满意度最高为目标函数，构建的峰谷分时电价及负荷优化模型表示如下：
[0054][0055]
其中，ω1+ω2＝1；ω1和ω2表征用户对削峰填谷和综合满意度的权重，minq和maxq-minq分别表示未实行峰谷分时电价前最小负荷和峰谷差值，minq
tou
和maxq
tou-minq
tou
分别表示实行峰谷分时电价后最小负荷和峰谷差值，二者做比值计算是为将其取值范围设定为1左右，以便与用户综合满意度ψ在同一水平比较；
[0056]
改进天鹰优化算法iao包括以下步骤：
[0057]
步骤1，算法初始化：
[0058]
步骤1.1，初始化种群过程中引入混沌映射，嵌入粒子之间的位置信息，使得搜素范围更广；设置种群数量为n，解空间维度为dim，最大迭代次数为miter，设置两个计数器c1＝0，c2＝0；初始化n组位置向量，第一组x1＝[x
11
,x
12
,
…
,x
1dim
]随机生成，剩下的n-1组由式：x
n+1
＝θxn(1-xn)计算得到，θ为变化因子，可根据θ的变化产生不同的混沌状态；初始化t＝0；
[0059]
步骤1.2，利用混沌映射初始化过程中，需要满足条件cos(xi,xj)≤ε，i，j＝1，2，
…
，n，i≠j；其中，cos(xi,xj)表示位置向量之间的距离，该值越小表示两个粒子之间越远，计算方式如下：
[0060][0061]
ε∈[0,1]为阈值，可凭经验和统计实验给定。
[0062]
步骤1.3，将初始化完成的n组位置向量在解空间[x
min
,x
max
]中进行映射；
[0063]
步骤2，计算种群的适应度值fitness，并对这些位置向量进行排序，初步确定全局最优解；
[0064]
步骤3，在每次迭代的过程中，天鹰的位置更新描述如下：
[0065]
步骤3.1，扩大搜索此时天鹰识别猎物区域，并通过垂直弯腰的高飞选择最佳的狩猎区域；为了增加种群的多样性，解决“早熟”问题，可在位置更新中加入余弦变化因子，数学模型如下：
[0066][0067]
其中，x1(t+1)为第一种搜索方法生成的t+1次迭代的解；x
best
(t)代表第t次迭代之前获得的最佳解，这反映了猎物的近似位置；rand是介于0和1之间的随机值；xm(t)表示在第t次迭代时当前解的平均值，计算方式如下：
[0068][0069]
步骤3.2，缩小搜索在第二种方法中，当天鹰从高空发现猎物区域时，天鹰在目标猎物上方盘旋，准备着陆陆地，然后攻击，这种方法称为短滑翔攻击的等高线飞行；在这里，ao狭窄地探索目标猎物的选定区域，为攻击做准备；该行为的数学模式如下式所示：
[0070]
x2(t+1)＝x
best
(t)
×
levy(dim)+xr(t)+(y-x)
×
rand
[0071]
式中，x2(t+1)是由第二个搜索方法生成的第t+1次迭代的解；levy(dim)是levy飞行分布函数，xr(t)是在第t次迭代时在[1,n]范围内获得的随机解；
[0072]
[0073]
式中，s＝0.01，u和v为介于0和1之间的随机数，β＝1.5，σ计算式如下：
[0074][0075]
x和y表示搜索中的螺旋形状，其中，x＝r
×
cos(θ)；y＝r
×
sin(θ)；r＝r1+u
×
d1；r1取1到20之间的值，用于固定搜索周期数，u＝0.00565，d1是从1到搜索空间维数dim的整数，ω＝0.005；
[0076]
步骤3.3，扩展开发在第三种方法中，当天鹰准确地指定了猎物区域，并且准备好着陆和攻击时，天鹰垂直下降并进行初步攻击，以试探猎物反应；这种方法称为低空飞行下降攻击；在这里，ao利用目标的选定区域接近猎物并进行攻击，该行为的数学模式如下式所示：
[0077]
x3(t+1)＝(x
best
(t)-xm(t))
×
α-rand+((ub-lb)
×
rand+lb)
×
δ
[0078]
式中，x3(t+1)是由第三种搜索方法生成的第t+1次迭代的解；α和δ是固定为较小值(0.1)的开发调整参数，ub和lb是位置向量上下界；
[0079]
步骤3.4，缩小开发在第四种方法中，当天鹰接近猎物时，天鹰根据其随机运动在陆地上攻击猎物，这种方法称为“行走并抓住猎物”，最后，ao在最后一个位置攻击猎物，该行为的数学模式如下式所示：
[0080]
x4(t+1)＝qf(t)
×
x
best
(t)-(g1×
x(t)
×
rand)-g2×
levy(d)+rand
×
g1[0081]
式中，x4(t+1)是由第四种搜索方法生成的第t+1次迭代的解；qf(t)表示在第t次迭代时用于平衡搜索策略的质量函数，g1表示在搜索猎物期间用于跟踪猎物的的各种运动，g2表示天鹰跟踪猎物的飞行速率；levy(d)是莱维飞行函数，x(t)是第t次迭代时的位置。
[0082]
质量函数计算式为：g1＝2
×
rand-1；飞行速率由线性递减修改为：
[0083]
步骤4，计算出更新后的适应度值，并且更新群体极值x
best
，如果此次迭代x
best
没有进行更新，则令c1＝c1+1；
[0084]
步骤5，评估算法是否存在早熟现象并修正；
[0085]
步骤5.1，若c1≥2，则c2＝c2+1，同时令c1＝0；
[0086]
步骤5.2，若c2≥γ，γ∈[5,10]，则令群体极值x
best
沿其负梯度方向进行更新，计算方式如下：
[0087][0088]
式中，为x
best
最近一次更新之前的值；
[0089]
步骤6，判断是否满足终止条件，若满足则输出最优解，结束程序；否则，重复以上天鹰优化算法流程继续进行寻优迭代处理。
[0090]
本发明的有益效果：
[0091]
通过与某地区原峰谷电价方案相比，基于本发明提出的方法峰谷时段划分更符合负荷曲线特征，利用改进的天鹰算法优化后的峰谷定价有效减少了最大负荷和负荷峰谷差，同时用户综合满意度较高。
附图说明
[0092]
图1为本发明iao算法优化负荷峰谷时段划分以及峰谷电价方法流程图；
[0093]
图2为负荷数据与优化后阶梯电价图；
[0094]
图3为pso算法优化迭代曲线图；
[0095]
图4为iao算法优化迭代曲线图；
[0096]
图5原负荷曲线与原峰谷电价下用户响应后负荷曲线比较图；
[0097]
图6原负荷曲线与优化后峰谷电价下用户响应后负荷曲线比较图。
具体实施方式
[0098]
图1为本发明iao算法优化负荷峰谷时段划分以及峰谷电价方法流程图。下面以一个具体实例说明本方法的实施流程，该实例以某用户实际负荷数据验证方法有效性。未实行峰谷电价前系统电价为0.49元/(kw
·
h)，实行峰谷电价后的峰平谷电价分别为0.658元/(kw
·
h)，0.49元/(kw
·
h)，0.358元/(kw
·
h),原峰谷时段划分结果为：24：00～7：00为谷段，8：00-11：00以及18：00～24：00为峰段，7：00～8：00以及11：00～18：00为平段。
[0099]
首先，采用模糊聚类分析方法，以各时刻的峰、谷隶属度x
i1
和x
i2
做为统计指标，经过标定以及聚类等步骤，得到峰、平、谷时段的聚类集合tf、t
p
和tg。然后运用集合分类思想，基于模糊聚类分析方法得出的基础时段划分结果，计算构造的阈值指标函数λ
tif
，进一步确定偏大型和偏小型半梯形隶属函数的最优阈值λ1和λ2。最后经过修正策略得出最终峰谷时段划分方案如表1所示。
[0100]
表1时段划分方案
[0101][0102]
得到最终峰谷时段的划分结果之后，利用电量电价弹性矩阵和建立的用户需求响应模型，以系统谷值负荷最大、负荷峰谷差值最小、用户综合满意度最高为目标函数，利用改进的天鹰优化算法获得优化后的峰谷电价结果如表2所示：
[0103]
表2峰谷电价制定结果
[0104][0105]
图2为负荷数据与优化后阶梯电价图。
[0106]
根据峰谷电价优化结果，进一步计算对模型的合理性及优势进行分析，下表3和表4给出了实施优化后的峰谷电价与原峰谷电价的指标对比数据。
[0107]
表3峰谷电价优化前后满意度结果对比
[0108][0109]
表4峰谷电价优化前后削峰填谷效果对比
[0110][0111]
本实施算例中算法参数取值如下：
[0112]
pso算法：粒子群群体大小为n＝100；维数dim＝2，最大迭代次数miter＝200。
[0113]
iao算法：天鹰群体大小为n＝100，维数dim＝2，最大迭代次数miter＝200，
[0114]
该实例用户为工业用户，由于其为三班制生产，工艺流程调整较为容易，且产品产值电耗较高，因此取用户综合满意度为：同时由于该用户在拉闸限电表中位置较靠前，故取ω1＝0.7，ω2＝0.3。
[0115]
采用本发明提出的改进天鹰优化算法(iao)优化负荷峰谷时段划分以及峰谷电价方法，并与粒子群算法(pso)优化结果进行对比，通过图3-图6的结果可知，本发明相比传统pso算法优化，收敛速度更快，寻优精度更高，通过表3和表4结果可知，优化后的分时电价比原峰时电价削峰填谷效果更好，用户满意度更高。
[0116]
最后说明的是，以上仅对本发明具体实施例进行详细描述说明。但本发明并不限制于以上描述具体实施例。本领域的技术人员对本发明进行的等同修改和替代也都在本发明的范畴之中。因此，在不脱离本发明的精神和范围下所作的均等变换和修改，都涵盖在本发明范围内。