一种Buck型DC-DC变换器的固定时间自适应参数估计方法

一种buck型dc-dc变换器的固定时间自适应参数估计方法
技术领域
1.本发明涉及buck型dc-dc电路系统和自适应参数估计的技术领域，具体涉及一种buck型dc-dc变换器的固定时间自适应参数估计方法。


背景技术：

2.dc-dc变换器具有效率高、体积小、稳定性高等优点，已广泛应用于直流电机驱动、计算机系统、通信设备等工业系统。dc-dc变换器是构成各种电力电子设备的基本电路单元，其稳定性对电力电子设备在一些高科技行业的应用起着至关重要的作用。随着新应用的不断发展，对dc-dc变换器的动态响应速度和稳定性精度的要求越来越高。
3.对于dc-dc转换器的许多应用，通常要求电路的参数精确已知，这是非常严格的，在实践中无法满足。例如，由于元件的老化，电路的参数，如电阻、电容和电感也可能随时间变化。此外，为了降低成本，电路元件的精度通常不高。在这种情况下，参数的使用值可能与实际值相差很大，这将严重影响其动态性能。准确的参数辨识不仅增加了原系统设计的难度，而且减少了参数误差对系统的影响，提高了系统的动态性能。近年来，参数识别问题在dc-dc功率电路的建模、估计、控制等许多最新发展中一直是基础。
4.现有的dc-dc变换器参数辨识算法大多只能实现渐近估计，其收敛速度和精度都不够。近年来，有限时间参数估计以其更快的收敛速度、更高的精度和更好的鲁棒性而备受关注。针对具有恒定功率负载的变流器，有学者提出了一种基于有限时间参数观测器的滑模控制器。然而，只有所考虑的输入电压参数是未知的。除此之外，对于具有未知输入电压和负载电阻的dc-dc降压转换器，有学者设计了两个观测器以在有限时间内估计未知参数。值得注意的是，对于渐近和有限时间参数估计算法，收敛时间取决于初始估计误差，并将随着初始误差的增加而增加。当初始误差的范围未知时，很难精确估计收敛时间。为了克服这个问题，提出了固定时间稳定性的概念。现有研究中关于dc-dc变换器固定时间参数估计的结果还很少。因此，如何开发一种新的算法来在固定时间内估计dc-dc降压变换器的参数是本发明的主要动机之一。
5.此外，现有的参数估计算法大多只适用于部分参数未知的电路系统。例如，只考虑未知电阻，或只考虑了未知输入电压。但是，在实际的电路系统中，电容、电感、电阻和输入电压等元件的参数都不容易准确地获得。因此，如何在没有电流传感器且元件参数未知的情况下，为dc-dc降压变换器开发一种新的估计算法是本发明的另一个重要动机。


技术实现要素：

6.根据上述提出的现有buck电路参数估计方法存在的一系列问题，本发明所提出的一种buck型dc-dc变换器的固定时间自适应参数估计方法能很好的克服这些缺陷，提供基于volterra积分算子的固定时间自适应参数估计算法，在仅有输出信号和pwm控制函数已知的情况下，保证参数估计值在一个不依赖于初始误差的固定时间内收到参数的真实值。通过在volterra积分算子中巧妙的选取核函数，该算法能够有效消除系统初始值的影响，
同时避免了对系统输出导数的计算。此外，不同于传统的自适应参数估计算法，本发明提出的代数参数估计算法能够实现参数的快速、准确估计。本发明的技术方案是，一种buck型dc-dc变换器的固定时间自适应参数估计方法，具体步骤如下：
7.s1、针对buck型dc-dc变换器，得出平均状态空间方程为：
[0008][0009]
其中c为滤波电容，l为滤波电感，r为负载电阻，v
in
为输入电压，v0为负载电阻输出电压，i
l
为电感电流，μ是pwm控制信号。
[0010]
s2、用x1＝v
ref-v0即表示为输出电压误差，根据平均状态空间方程，可以得到：
[0011][0012]
为了方便参数估计器设计，将方程在根据输出y的函数进行改写，得到：
[0013][0014]
将用θ1表示，用θ2表示，用θ3表示，y-v
ref
用y2表示，μ用y3表示，y用y1表示，得到：
[0015][0016]
那么对的估计转变为对θ1、θ2、θ3的估计。
[0017]
s3、选取核函数k(t，τ)来决定了volterra积分算子的映射[vkf](t)效果：
[0018][0019]
其中ωh，ω＞0为设计参数。将其展开得到：
[0020][0021]
其中f
p
(τ)，p＝0，1，2满足：
[0022][0023]
公式(7)可以计算满足：
[0024][0025]
公式(6)和公式(8)可以得到核函数关于的导数满足：
[0026][0027]
可以得到对于有k(i)(t，t)＝0，k(i)(t，0)＝0。
[0028]
s4、对系统方程(4)进行volterra积分算子的映射，消去未知量；
[0029]
首先，对volterra积分算子进行如下定义：
[0030]
定义为到的希尔伯特空间内的局部平方可积函数。函数f(t)经过volterra积分算子进行映射定义：
[0031][0032]
公式(10)中k(
·
，
·
)：希尔伯特-施密特核函数。
[0033]
定义为f(t)的i阶导数，则[vkf(i)](t)可以展开成：
[0034][0035]
其中k(i)(
·
，
·
)表示k(
·
，
·
)关于第二个变量的i阶导数。
[0036]
然后，对系统(4)两边同时进行积分算子vk运算可得：
[0037][0038]
尽管y1，y2，y3是已知的，但其导数是未知的，因此是未知的。使用定义中的公式(11)，可得：
[0039][0040]
代入原式(12)得：
[0041][0042]
公式(14)除了θ1，θ2，θ3外，其他变量均是已知，因此可以用来设计参数观测器。
[0043]
s5、设计观测器，对被估计量进行精确估计；
[0044]
给出定义：
[0045]
对构造微分方程：
[0046][0047]
其中可由公式(9)获得。若核函数k(t，τ)满足公式(5)，那么对成立。
[0048]
可得因此(14)可以重新写为：
[0049][0050]
为了方便估计器得设计，(16)可以重新写为：
[0051]
s(t)＝v(t)θ，(17)
[0052]
其中
[0053][0054]
为了设计自适应参数估计器，v(t)需要满足如下得可激励假设：
[0055]
函数v(t)满足持续可激励条件，即存在常数r＞0，t0＞0使得如下不等式对成立：
[0056][0057]
将(17)左乘v
t
(t)可得：
[0058][0059]
其中
[0060][0061]
对(20)等式两边同时进行积分算了运算，其中kg＝e-g(t-τ)
，g＞0，则可得：
[0062]s1，f
(t)＝v
1，f
(t)θ，(21)
[0063]
其中通过求导容易证明，变量s
1，f
(t)v
1，f
(t)可由如下系统产生：
[0064][0065]
定义如下辅助变量：
[0066][0067]
其中为自适应估计参数，其更新率由以下公式给出：
[0068]
自适应参数的更新率为：
[0069][0070]
其中min{eig(v
1，f
(t))}表示v
1，f
(t)特征值的最小值，若假设1成立，且自适应更新率中的参数满足g＞0，α1＞0，α2＞0。
[0071]
s6、在buck电路仅在输出电压与pwm函数已知的情况下，保证参数估计值在一个不依赖于初始误差的固定时间内收到参数的真实值；
[0072]
存在一个不依赖误差的固定时间t
max
使得成立，其中t
max
估计值为：
[0073][0074]
本发明与现有技术相比，具有如下优点与有益效果：
[0075]
第一、本发明和已有的基于渐进收敛和有限时间收敛的参数估计方法相比，本发明使用的固定时间收敛方法收敛时间短、收敛精度高，还不受参数初始值估计误差的影响。
[0076]
第二、本发明所提出方法是对buck型dc-dc变换器上所有系统参数进行估计，很好的处理了部分参数估计所带来的估计误差。
[0077]
第三、本发明所使用的volterra积分算子，能够有效消除了系统初始值的影响，同时避免对系统输出导数的计算，使得所提算法只需用到系统的输出信息，因此能够有效减少传感器的使用，从而有效降低算法的实现成本。
附图说明
[0078]
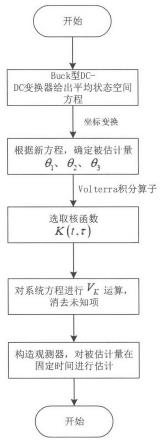
图1为本发明一种buck型dc-dc变换器的固定时间自适应参数估计方法的设计流程图。
[0079]
图2为本发明buck型dc-dc变换器的电路原理图。
[0080]
图3为本发明估计方法在自适应初值为下，估计值与真实值的误差效果图。
[0081]
图4为本发明估计方法在自适应初值为下，估计值与真实值的误差效果图1。
[0082]
图5为本发明估计方法在不同初始估计误差的收敛时间。
具体实施方式
[0083]
为了使本发明的设计思路以及理论更加清楚，下面将从buck型dc-dc电路自适应参数估计方法的建立、设计、原理以及证明这几个方面进行详细说明，以下将结合附图说明
中的附图进行详细说明。
[0084]
如图1所示，本发明提供一种buck型dc-dc变换器的固定时间自适应参数估计方法。按照本发明的设计，根据buck型dc-dc变换器设计的自适应参数估计能在不依靠初始时间的条件下，在固定时间内精确估计参数值。本发明的技术方案具体步骤如下：
[0085]
步骤1、如图2所示为buck型dc-dc变换器系统原理图，由一个直流输入电压源、一个半导体开关s、一个二极管d、一个滤波电容c、一个滤波电感l和一个负载电阻r组成。将输入电压定义为v
in
，负载电阻输出电压为v0，电感电流为i
l
，μ是pwm控制信号。buck型dc-dc变换器可以用平均状态空间方程表示为：
[0086][0087]
用v
ref
表示期望参考电压，那么x1＝v
ref-v0即表示为输出电压误差。根据平均状态空间方程，可以得到：
[0088][0089]
为了方便参数估计器设计，将系统(2)关于输出y的函数进行改写，得到：
[0090][0091]
将用θ1表示，用θ2表示，用θ3表示，y-v
ref
用y2表示，μ用y3表示，y用y1表示，得到：
[0092][0093]
那么对的估计转变为对θ1、θ2、θ3的估计。
[0094]
步骤2、核函数k(t，τ)的选取决定了volterra积分算子的映射[vkf](t)效果，本文选取核函数为：
[0095][0096]
公式(5)中ωh，ω＞0为设计参数。将展开得到：
[0097]
[0098]
其中f
p
(τ)，p＝0，1，2满足：
[0099][0100]
公式(7)可以计算满足：
[0101][0102]
公式(6)和公式(8)可以得到核函数关于的导数满足：
[0103][0104]
公式(8)与公式(9)可以得到对于有k(i)(t，t)＝0，k(i)(t，0)＝0。
[0105]
步骤3、首先，对volterra积分算子进行如下定义：
[0106]
定义为到的希尔伯特空间内的局部平方可积函数。函数f(t)经过volterra积分算子进行映射定义：
[0107][0108]
公式(10)中k(
·
，
·
)：希尔伯特-施密特核函数。
[0109]
定义为f(t)的i阶导数，则[vkf(i)](t)可以展开成：
[0110][0111]
其中k(i)(
·
，.)表示k(
·
，.)关于第二个变量的i阶导数。
[0112]
然后，对系统(4)两边同时进行积分算子vk运算可得：
[0113][0114]
尽管y1，y2，y3是已知的，但其导数是未知的，因此是未知的。使用定义中的公式(11)，可得：
[0115][0116]
代入原式(12)得：
[0117][0118]
公式(14)除了θ1，θ2，θ3外，其他变量均是已知，因此可以用来设计参数观测器。
[0119]
步骤4、设计观测器，对被估计量进行精确估计；
[0120]
给出定义：
[0121]
对构造微分方程：
[0122][0123]
其中可由公式(9)获得。若核函数k(t，τ)满足公式(5)，那么对成立。
[0124]
可得因此(14)可以重新写为：
[0125][0126]
为了方便估计器得设计，(16)可以重新写为：
[0127]
s(t)＝v(t)θ，(17)
[0128]
其中
[0129][0130]
为了设计自适应参数估计器，v(t)需要满足如下得可激励假设：
[0131]
函数v(t)满足持续可激励条件，即存在常数r＞0，t0＞0使得如下不等式对成立：
[0132][0133]
将(17)左乘v
t
(t)可得：
[0134][0135]
其中
[0136][0137]
对(20)等式两边同时进行积分算子运算，其中kg＝e-g(t-τ)
，g＞0，则可得：
[0138]s1，f
(t)＝v
1，f
(t)θ，(21)
[0139]
其中通过求导容易证明，变量s
1，f
(t)v
1，f
(t)可由如下系统产生：
[0140][0141]
定义如下辅助变量：
[0142][0143]
其中为自适应估计参数，其更新率由以下公式给出：
[0144]
自适应参数的更新率为：
[0145][0146]
其中min{eig(v
1，f
(t))}表示v
1，f
(t)特征值的最小值，若假设1成立，且自适应更新率中的参数满足g＞0，α1＞0，α2＞0。存在一个不依赖误差的固定时间t
max
使得成立，其中t
max
估计值为：
[0147][0148]
证明：第一步：证明辅助变量r
1，f
(t)能够在固定时间内收敛到零。对r
1，f
(t)求导可得：
[0149][0150]
根据v
1，f
(t)的定义与假设1可以得到，当t≥t0：
[0151][0152]
根据公式(27)可知，
[0153][0154]
对于成立，因此有
[0155][0156]
将公式(29)与(22)带入公式(26)可得：
[0157][0158]
其中定义
[0159]r1，f
(t)＝[r1(t)，r2(t)，r3(t)]
t
ꢀꢀꢀ
(31)
[0160]
那么公式(30)可以写成如下四个标量系统：
[0161][0162]
选取lyapunov函数：
[0163][0164]
对vi求导可得
[0165][0166]
可引理1可知成立，即
[0167][0168]
成立，其中t
max
满足公式(31)。
[0169]
第二步，证明一旦辅助变量r
1，f
(t)＝0，有
[0170]
由公式(28)可知，r
1，f
(t)＝0时，有
[0171][0172]
将公式(26)和(36)相减可得：
[0173][0174]v1，f
(t)可逆且大于零，因此可得：
[0175][0176]
由此可以证明自适应参数更新率定理成立。
[0177]
实施例
[0178]
为了验证本发明有效性，本节将buck型dc-dc变换器系统运用本发明提出的估计算法进行仿真验证。对buck型dc-dc电路系统参数选取如表1所示。固定时间自适应参数估计算法按照(24)进行设计，其参数选择如表2所示。
[0179]
为了验证算法的固定时间收敛性，分别选取两个不同的自适应初始值：
[0180][0181][0182]
来进行算法的仿真验证。
[0183]
表1
[0184][0185]
表2
[0186][0187]
仿真结果如图2-4所示。收敛时间的估计可由(25)计算，收敛时间为t
max
≈1.789s。两种不同初值下估计误差分别如图2和图3所示。从图中可以清楚地得出结论，图2和3表明，本发明所提算法即使在不同的初始误差下，也可以实现在固定时间不大于t
max
≈1.789s内精确估计系统参数。这自然也可以从图4中看出，其中从图4可以清楚地看出随着初始误差不断增大，收敛时间逐渐趋近平稳，也就说明本发明所提出的估计方法的收敛时间不存在初始估计误差。
[0188]
本发明提出了一种buck型dc-dc变换器的固定时间自适应参数估计方法。与传统的渐近估计和有限时间估计算法相比，所提出的方法可以在固定时间内达到精确估计参数并且不受初始估计误差影响。
[0189]
所应该理解的是，以上所述仅为本发明的一般步骤，并不用于限制本发明，凡是在本发明的精神和原则之内所作的任何修改和等同替换、改进等，均应保安在本发明的保护范围之内。