一种基于单调控制系统理论的电力系统低频减载有效性判别方法

1.本发明属于电网动态特性分析技术领域，具体涉及一种基于单调控制系统理论的电力系统低频减载有效性判别方法。


背景技术：

2.随着新能源占比的不断提高，系统电力电子化特征愈发凸显，给电力系统的频率特性带来重大影响。电力系统频率响应能力主要由系统的转动惯量与调频能力决定，由于新能源一般通过电力电子换流器和电网接口，在常规控制下其输送功率与电网频率解耦，不具备传统电机按照惯性时间常数分配扰动功率的能力，不能主动响应电网频率变化，从而不具备惯量及一次调频能力，使得系统频率调节能力变差。并且，新能源出力受电压影响显著，在出现扰动时进一步恶化系统频率特性，导致系统频率快速跌落或飙升，可能触发低频减载，严重时甚至会造成系统解列。为提升高占比新能源电网频率认识水平，迫切需要提高对其频率稳定分析方法的研究。
3.目前对频率稳定分析方法主要有三种：
①
时域仿真法；
②
模型分析法；
③
机器学习法。时域仿真法是将电力系统等效为一组微分代数方程，用仿真软件时域仿真，得到扰动后系统的频率变化曲线，判断频降最低点、频率变化率等关键指标是否越限。模型分析法通过对时域仿真的详细模型进行合理的假设和简化，进而建立表征频率动态特征量的解析化表达式，求解频率特征。机器学习法指通过数值仿真获得的样本数据进行特征提取和离线学习，然后将预想故障及运行数据输入已训练好的机器学习模型，以实现频率响应快速计算。
4.时域仿真法可利用详细的系统频率模型，计算结果精度相对较高，具有较好可扩展性，但存在计算量大、耗时长的特点，并且由于新能源加入，电网不确定因数增加，复杂度更高，系统更难以满足频率安全在线评估需求。机器学习法的样本数据必须由数值仿真获得，其精度本质上还是依赖于时域仿真计算。此外，上述两种方法对电网的可解释性和泛化能力较弱。对于给出系统频率动态及相关参数的解析关系，以及获得电网一些规律性和解析性结论，主要依靠模型分析法。
5.模型分析法中，为提升稳定分析效率，通常采用平均系统频率(average system frequency,asf)模型和系统频率响应(systen frequency response,sfr)模型。这两种模型都具有降低系统规模，计算量小以及直观快速地求解频率特征的特点，但两种模型都忽略了电压动态变化、网络拓扑和机组之间的影响，以及频率与功角、电压之间的耦合关系。例如当机组间频率振荡或系统电压发生较大偏移时，计算结果与真实值之间往往存在较大偏差。只有当系统采用全状态模型，即综合考虑机组、负荷、网络以及控制器的动态特性，才能在保证电网的规律性和解析性的同时获得更高的精确度。
6.在数学分析层面上，人们对系统动态行为的认识和研究不断深入，出现了不少新的分析方法和工具，其中运用单调控制理论，提出了输入输出单调的判定条件，通过引入时间断面积分的概念，避免了代数变量与状态变量间交替求解的过程，并为电力系统动态电
压问题提供了一种新颖的数学分析工具。并通过采用全状态模型，综合考虑频率与功角、电压间的相互作用，尽可能真实分析在扰动作用下系统的动态行为。


技术实现要素：

7.有鉴于此，本发明提供了一种基于单调控制系统理论的电力系统低频减载有效性判别方法，通过对电力系统数学模型进行处理与分析，确定系统的输入输出判定表达式，并分析其符号特征，以此判断电力系统是否具备单调性，验证系统低频减载在具体场景下的有效性，且通过灵敏度分析，了解电网内部相关变量之间具体数学关系，有助于指导电网故障时的参数控制。
8.为了实现上述目的，本发明采用如下技术方案包括以下步骤：
9.s1：确定电力系统所采用的全状态频率分析数学模型，并根据建立的数学模型得到系统频率表达式，从而得到决定频率变化的控制变量和状态变量；
10.s2：构造电力系统输入输出判定表达式δh，并根据δh求微分得到输出量变化量δh
′
表达式，依据数学性质分析判定式δh
′
中状态分量和控制分量的表达式，结合δh
′
对各状态变量和δh
′
对控制变量的变化曲线得到δh
′
图像；
11.s3：对步骤s2的δh
′
图像从初始时刻到t时刻进行积分，得到原输出判定表达式δh的符号特征，并根据符号特征判断系统是否为单调系统。
12.所述步骤s1中全状态频率分析数学模型的确定方法具体为：
13.由于同步发电机采用三阶模型，可将同步发电机机端节点用暂态电抗后的暂态电势节点代替，并将等值导纳并入网络节点电压方程得到一个包含电势节点的网络节点电压方程：
[0014][0015]
式中：y
gg
、y
gl
、y
lg
、y
ll
为计及同步发电机暂态电抗的分块导纳矩阵，下标g、l分别代表同步发电机和负荷；ig为同步发电机节点注入电流；
[0016]
将包含电势节点的网络节点电压方程分块展开，消去负荷节点电压u
l
得节点注入电流ig关于同步发电机q轴内电势向量eq′
的表达式：
[0017][0018]
式中：y
′
为简化导纳矩阵，
[0019]
借助xy坐标系与dq坐标系之间的转化公式，对ig＝y
′eq
′
进行坐标变化得dq坐标系下电流id、iq与电磁功率pe关于同步发电机q轴内电势向量eq′
的显式表达式：
[0020][0021][0022]
[0023]
式中：n为同步发电机总数，i和j为同步发电机的编号；g
ij
、b
ij
为简化导纳矩阵y
′
的实、虚部；δ
ij
为暂态电势之间功角差；p
ei
是第i台同步发电机的电磁功率；
[0024]
将电磁功率表达式代入电力系统的微分方程，消去电力系统的代数方程，得到电力系统的全状态频率分析数学模型：
[0025][0026]
所述步骤s1中得到决定频率变化的控制变量和状态变量的方法具体为：
[0027]
根据全状态频率分析数学模型中的第二个公式，可得第i台同步发电机频率表达式为：
[0028][0029]
由同步发电机频率表达式可得，决定频率变化的控制变量为负荷节点切载比率u，状态变量为机械功率pm、同步发电机功角δ、q轴暂态内电势e
′q。
[0030]
电力系统由一组微分方程和代数方程构成：
[0031]
考虑励磁调节以及一阶原动机调速器模型的三阶同步发电机模型，并忽略凸极效应，不考虑转速变化因素对转子运动方程的影响，微分方程具体为：
[0032][0033]
式中：δ是同步发电机功角向量，ωs、pm分别为同步发电机标称转速和输入机械功率构成的矩阵；p
sv
、pc、pm分别为汽室输入功率、功率改变值、机械功率值对角矩阵，t
sv
为调速器的时间常数，t
ch
为汽室的时间常数，为调速器增益矩阵，其中rd为静调压系数对角矩阵；eq′
为同步发电机q轴内电势向量，e
fd
是励磁电压向量，v
ref
为电压调节内部参考值对角矩阵，td′o为发电机d轴暂态时间常数对角矩阵，ka和ta分别是一阶励磁调节器的比例系数和时间常数对角矩阵；
[0034]
对于代数方程部分：
[0035]
考虑负荷为恒阻抗类型，负荷的等值导纳y
l
为：
[0036][0037]
式中：s
*
为负荷节点注入功率的共轭，v
l
为负荷节点电压。
[0038]
将同步发电机机端节点用q轴内电势节点代替，并将等值导纳并入网络节点电压方程得到代数方程：
[0039][0040]
所述步骤s2具体为：
[0041]
根据步骤s1的系统频率表达式以及对应的控制变量和状态变量，构造电力系统的输入输出判定表达式：
[0042][0043]
式中：x1、x2分别为t时刻对应于不同控制变量u1、u2的状态变量；
[0044]
由于上式的符号特征涉及积分后求导，且没有关于积分项的显式表达式。为简化分析，可先判断积分号内表达式在任意t时刻不同切载比率下输出量变化量h
′
，通过判断其大小，再从初始时刻到t时刻积分，从而近似上式是否满足单调保序条件：
[0045]
根据δh求微分得到输出量变化量δh
′
表达式：
[0046][0047]
依据数学性质分析判定式δh
′
中状态分量和控制分量的表达式，得t时刻输出量变化量δh
′
对应某台同步发电机机械功率、同步发电机q轴内电势和同步发电机功角的灵敏度表达式为：
[0048][0049][0050][0051]
根据各个灵敏度表达式得变化量δh
′
对各状态变量的变化曲线，通过差分法求得变化量δh
′
对控制变量的变化曲线；结合δh
′
对各状态变量和δh
′
对控制变量的变化曲线得到δh
′
图像。
[0052]
所述步骤s3具体为：
[0053]
对步骤s2中的δh
′
图像进行零时刻到t时刻的积分，得到原输出判定表达式δh的符号特征；
[0054]
当h(t,x2,u2)-h(t,x1,u1)≥0成立时，则系统为单调系统，满足保序特征，此时可采用低频减载处理故障；
[0055]
当h(t,x2,u2)-h(t,x1,u1)≥0不成立时，此时低频采取减载措施不利于频率恢复，建议采取其他措施恢复频率。
[0056]
本发明的有益效果：
[0057]
本发明通过对电力系统数学方程模型进行处理与分析，构建系统频率的表达式，确定其相关控制变量和状态变量，再由推导的输入-输出判定条件给出判定表达式，分析其符号特征，从而判断系统是否具有单调性，为电力系统动态电压问题提供了一种新颖的数学分析工具。此外，系统利用全状态模型分析，即综合考虑机组、负荷、网络以及控制器的动态特性，保证了电网的规律性和解析性的同时获得更高的精确度。并利用灵敏度分析，了解电网内部相关变量之间相关关系，有助于指导电网故障时的参数控制。
附图说明
[0058]
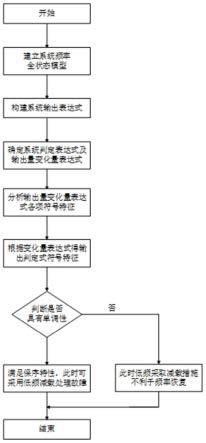
图1为本发明提供的一种基于单调控制系统理论的电力系统低频减载有效性判别方法流程示意图；
[0059]
图2为本发明提供的两节点系统拓扑示意图；
[0060]
图3为本发明提供的单机系统在不同切载比率下偏导的动态变化曲线示意图。
[0061]
图4为本发明提供的单机系统在不同切载比率下偏导的动态变化曲线示意图。
[0062]
图5为本发明提供的单机系统在不同切载区间下输出变化量判定式的各项取值；其中图(a)为机械功率项；图(b)为暂态电势项；图(c)为控制变量项。
[0063]
图6为本发明提供的单机系统在不同切载区间下输出变化量判定式的变化曲线示意图。
[0064]
图7为本发明提供的多机系统在不同切载比率下频率变化量-暂态电势灵敏度dh
′
/deq′
的时域变化曲线示意图；其中图(a)为切载20％；图(b)为切载60％。
[0065]
图8为本发明提供的多机系统在不同切载比率下频率变化量-暂态电势灵敏度dh
′
/dδ的时域变化曲线示意图；其中图(a)为切载20％；图(b)为切载60％。
[0066]
图9为本发明提供的多机系统机械功率差实际值与计算值对比图；
[0067]
图10为本发明提供的多机系统不同切载区间下输出变化量判定式的各项取值；其中图(a)为机械功率项；图(b)为暂态电势项；图(c)为功角项；图(d)为控制变量项。
[0068]
图11为多机系统输出量变化量判定式的计算结果；
[0069]
图12为多机系统输出量变化量判定式的仿真结果；
[0070]
图13为多机系统不同切载比率下频率特性曲线；
[0071]
图14为机电暂态仿真软件psd-bpa提供的光伏一次调频控制模型；
[0072]
图15为替换节点3为光伏的三机九节点系统结构图，序号1～9分别表示9个节点；
[0073]
图16为本发明提供的考虑新能源光伏接入时输出量变化量判定式的计算结果和仿真结果对比图；
[0074]
图17为本发明提供的考虑新能源光伏接入时不同切载比率下频率特性曲线；
[0075]
图18为藏中电网三相短路故障后在不同切载比率下频率恢复特性曲线。
具体实施方式
[0076]
下面将结合本发明实施例中的附图，对本发明实施例中的技术方案进行清楚、完整地描述，显然，所描述的实施例仅仅是本发明一部分实施例，而不是全部的实施例。基于本发明中的实施例，本领域普通技术人员在没有做出创造性劳动前提下所获得的所有其他实施例，都属于本发明保护的范围。
[0077]
本发明实施例公开了一种基于单调控制系统理论的电力系统低频减载有效性判别方法，如图1所示，包括以下步骤：
[0078]
s1.确定电力系统所采用的全状态频率分析数学模型，并根据建立的数学模型得到系统频率表达式，得到决定频率变化的控制变量和状态变量；
[0079]
s2：构造电力系统输入输出判定表达式δh，并根据δh求微分得到输出量变化量δh
′
表达式，依据数学性质分析判定式δh
′
中状态分量和控制分量的表达式，结合δδh
′
对各状态变量和δh
′
对控制变量的变化曲线得到δh
′
图像；
[0080]
s3：对步骤s2的δh
′
图像从初始时刻到t时刻进行积分，得到原输出判定表达式δh的符号特征。判断δh是否恒大于等于零，若成立，则系统为单调系统，控制量和输出量满足保序特征，论证低频减载方法的有效性。
[0081]
在本实施例中，通过三种电力系统场景来验证电力系统低压减载时为单调系统：
[0082]
(1)单机单负荷系统
[0083]
在一个单机单负荷系统中，假设同步发电机采用三阶模型，发电机机端节点能用暂态电抗后的内电势节点替代，假设负荷均为恒阻抗类型，其示意图如图2所示，设置发电机调速器参数如表1所示，并取外接电抗(包括变压器和输电线路的电抗)xe＝0.1 pu，负荷为恒阻抗类型，取有功为80mw，无功为60mw；系统基准容量sb＝100mva，发电机容量等于系统基准容量。
[0084]
表1
[0085][0086]
令x指代为系统的状态变量，由前单机系统全状态模型可知其包含汽室输入功率、机械功率、同步发电机功角δ、转速ω、q轴暂态电势eq′
、励磁电压e
fd
；令控制变量(输入量)u表示负荷节点切载比率，输出变量y表示系统频率系统数学模型是：
[0087][0088]
首先分析代数部分，根据电路方程得到考虑减载比率的负荷电压解析表达式：
[0089]
[0090]
式中：r
l
+jx
l
为等值负荷阻抗。
[0091]
令xu＝(1-u)(x
′
+x1)+x
l
，负荷电压幅值表达式可化简为：
[0092][0093]
从而用空载电势eq′
表示的电磁功率方程式可写为：
[0094][0095]
对于稳态平衡点，将对应微分方程式左端项置零，得到输出量表达式：
[0096][0097]
由上式可知稳态频率取值的变化量由系数k1、暂态电动势e
′q和暂态电动势和负荷节点电压相角差的正弦值sinα决定，其随切载量变化值如表2所示。
[0098]
表2
[0099][0100][0101]
由表1数据可知，看出系数k1随切载比率的增加而上升，逐渐趋近于1；e
′q与sinθ均随切载比率的增加而下降，切载后频率值的稳态平衡点随切载比率的上升而增加
[0102]
在频率稳定问题中，除了需要讨论稳定平衡点外，厘清频率在过渡过程的移动过程具有重要意义。对于不同输入量对频率输出量的影响，其输出方程由转子运动方程决定，其表达式如下所示：
[0103][0104]
由上式可知，过渡过程输出量和状态变量机械功率pm、暂态电动势e
′q和控制变量切载量u相关。
[0105]
考虑具体的两节点系统减载场景，构造一个如下所示的输入输出系统：
[0106][0107]
结合输入输出判定条件，不同输入量(切载比率)u2》u1，在t时刻下的输出量(负荷电压)可以表示为：
[0108][0109]
式中：积分项中偏导函数的括号内信息表示取值点位置。
[0110]
由于上式的符号特征涉及到积分后求导，且没有关于积分项的显式表达式。为简化分析，可先判断积分号内表达式在任意t时刻不同切载比率下输出量变化量δh
′
，如下式所示。
[0111]
通过判断其大小，再从初始时刻到t时刻积分，从而近似上式是否满足单调保序条件。
[0112][0113]
由上述输出量变化量表达式，得到输出量的变化量t时刻单调性判定条件为：
[0114][0115]
其中t时刻输出量变化量h
′
对应各状态变量灵敏度表达式如下所示：
[0116][0117][0118]
设置在0.5s时切除不同比例有功无功负荷。对于输出变化量-机械功率灵敏度由表达式可知其值为常数，且恒为正值。对于在不同切载比率其灵敏度变化如图3所示，其值恒小于零。输出变化量-暂态电势灵敏度大小与系数k1、暂态电势eq′
、负荷节点电压相角差θ及当前时刻暂态电势幅值相关，而系数k1和暂态电势和负荷节点电压相角差θ在切载时突变，因此该灵敏度结果相应地在切载后突变。此外，灵敏度的元素符号固定，说明系统两变量之间相互作用明确，例如机械功率的增加提升系统频率的上升，符合传统同步发电机特性。
[0119]
对于灵敏度，因切载比率和所有状态变量均相关，其关于频率的显式表达
式求解难度大。下面通过差分法分别计算输出量和输出量的变化量对输入量偏导：和结果如表3所示：
[0120]
表3
[0121][0122]
对于输出量的变化量判定表达式中机械功率差值，可同样根据微积分基本公式，时域响应差值p
m2
(t,u2)-p
m1
(t,u1)关于初值差存在如下的积分表达式：
[0123][0124]
注意到t
ch
＝0.2s，t
sv
＝0.02s，可近似认为t
ch
》》t
sv
。如果考虑再热器系统，一般再热器时间常数为6～12s，此时t
ch
将更大。因此，在求解机械功率变化的主要特征时，可近似忽略调速器调节过程，从而获得如下所示的降阶模型：
[0125][0126]
从而可得到：
[0127][0128]
可以看成是下述初值问题的解：
[0129][0130]
对于一阶微分方程，稳态时取最小值：
[0131][0132]
借助仿真数据，得到时域变化结果，如图4所示。其最后稳态值经过上式求出的与表3数据比较，两者数值基本一致，可验证上式的有效性。
[0133]
对于暂态电势差值，直接通过时域数据可得。从而通过以上分析，对输出量的变化量的判定表达式中关于积分变量的函数，在输入量相差不大的情况下，可近似取被积函数变量中值，从而将偏导结果视为恒定进行积分估算，其表达式为：
[0134][0135]
上式中状态变量项和控制变量项在不同切载区间的时域变化如图5(a)-(c)所示。
[0136]
由图5可见，任意t时刻机械功率作用项恒为负值，说明了机械功率具有维持系统频率不变的作用，可以提升频率稳定性；暂态电势对频率变化量的作用，说明电力系统频率动态和电压动态的相互耦合，相互作用；控制分量对频率变化量的影响恒为正，说明切载比
率和频率呈正相关性，且有切载比率越高，频率上述速率越快。其次，通过纵向对比，可知输出频率的变化量的正负性质主要由机械功率和控制变量决定。
[0137]
根据图5数据，相加求得输出变化量的曲线如图6所示，对频率的变化量进行时域积分，即可近似输出判定表达式的符号特征；由图6可知，面积先增后减，且正值面积明显大于负值部分，从而可得输出判定表达式恒大于零，系统为单调系统且保序关系成立。对图6进一步分析，发现在初始切载区间比率越大，其尖峰值越大，对应频率变化速度越快。
[0138]
(2)多机系统
[0139]
以10机39节点系统为例，此时系统全微分方程为：
[0140][0141]
由此可得可得第i台发电机输出表达式：
[0142][0143]
相比于一台发电机频率变化情况，电力系统往往更关注全系统动态频率的变化过程。通常可假设全网频率差异不大，利用惯量中心的等效频率来反映系统整体频率变化，即惯量中心频率
[0144][0145]
从而系统频率输出量表达式：
[0146][0147]
在任意t时刻，对应不同输入量u1、u2(u2》u1)时，得到多机输入输出的判定表达式：
[0148][0149]
式中：积分项中偏导函数的取值点为x1+r(x
2-x1)，其中x可代指状态变量机械功率暂态电动势幅值功角δi以及控制变量切载比率u。
[0150]
参考单机系统分析，得任意t时刻不同切载比率下输出量的变化量δh
′
表达式：
[0151][0152]
从而其输出量的变化量δh
′
对应判定表达式为：
[0153][0154]
根据上式可求得t时刻输出量变化量δh
′
对应某台发电机灵敏度表达式为：
[0155][0156][0157][0158]
式中：输出变化量-机械功率灵敏度的机械功率为发电机侧量，以电网侧为基准时需要标幺值换算。
[0159]
设置负荷节点8在0.5s时切除不同比率有功无功负荷，各输出变化量对状态变量灵敏度值如表4及图7和图8所示。仍是恒为正值的常数，表明机械功率增加，会使频率变化量增大，且发电机额定容量越大，其对频率变化量影响越大。对于频率变化量-暂态电势灵敏度在正常及减载时，频率变化量和暂态电势呈负相关，以电压升高为例，此时对应系统负荷所需要无功增加，负荷有功和线路损耗有功增加以增大电磁功率，使得转子运动方程不平衡功率增加，从而频率下降。频率变化量-功角灵敏度恒为正，由于机组转子角是机组转速/频率的积分，从而频率的变化量对于功角可理解为二次积分，从而具有一致性。对于与单机系统类似，可采取数值计算差分法求得，如表5所示
[0160]
表4
[0161][0162]
表5
[0163][0164]
对于状态变量机械功率差值随输入差值的变化规律，由于调速器原动机模型与单机系统一致，因此单机系统推导结论式可应用于多机系统。通过时域仿真，对比10台发电机
仿真的实际差值与单机系统推导右端项如图9所示，其实际差值与计算差值基本一致。
[0165]
对于输出量变化量判定式中状态变量暂态电势幅值eq
′
以及功角δi在不同切载比率的值，通过时域仿真可得其数值。该算例下，变化量判定式各状态变量或控制变量的在不同切载比率时的大小值见附录图10，其作用与单机系统类似。对于暂态电势幅值与功角，受扰时通常一起变化，两项之和幅值更小，从而变化量判定式的正负的决定项依然由机械功率和控制变量切载比率决定，但也与暂态电势与功角有关，说明了实际电力系统功角、电压、频率等在动态过程中的相互耦合。
[0166]
图11展示了输出量变化量判定式的符号特征，图12展示了频率变化量的时域结果。通过对比，两者数量级一致，验证了输出量变化量判定式的正确性。注意到其计算结果与仿真结果相比，波动性更小，这是因为在式输出量变化量判定式计算时将减载区间任意一点的积分值的偏导结果视为恒定。通过对输出变化量求积分，可知式输出量判定式恒大于零，系统单调保序得证。具体的切载保序结果见图13。
[0167]
(3)新能源机组低频减载过程单调保序分析
[0168]
由于新能源渗透率的不断提高，给电网的频率稳定问题带来了新的挑战。目前，对光伏参与调频分析可分为以下三个类型：一是光伏系统运行于最大功率点并不参与系统调频；二是通过控制光伏阵列电压，使其减载运行，留有一定的减载调频备用；三是利用虚拟同步发电机技术，使光伏能模拟同步发电机参与调频。而对于bpa中光伏模型，其主要采用前两种。
[0169]
若光伏不参与系统调频时，其在故障和恢复期间均可等效为恒功率负荷，从而可直接采用多机系统的输出判定表达式方法进行分析验证。
[0170]
若光伏考虑减载备用时，参考机电暂态仿真软件psd-bpa用户手册，其一次调频控制模型如图14所示，可等效为下垂控制环节。此时光伏输出功率随频率变化而变化，在故障过程中由恒功率负荷变为变功率负荷，如频率下降时增大输入功率以抑制频率下降。仅需将变功率负荷以动态导纳矩阵的形式并入网络方程即可，从而系统频率输出表达式形式并未改变，因此仍可利用多机系统的输出判定表达式进行分析。
[0171]
因此，对于bpa中采用的光伏模型，均可利用前述多级系统保序证明过程进行证明。
[0172]
由上述三种三种电力系统场景，通过算例进行验证与分析。
[0173]
具体实施例：
[0174]
(1)三机九节点系统
[0175]
考虑新能源高占比接入场景，在三机九节点系统中将节点3所连机组用等量光伏代替，渗透率达到26.61％，如图15所示，同时假定光伏电站采用最大功率点跟踪控制。
[0176]
在节点5切载时利用输出量变化量判定式得到计算结果与仿真结果对比见图16，验证了单调保序判定条件应用在含新能源系统的有效性。并由图16可知，判定表达式恒大于零，系统满足保序特征。
[0177]
同理可得系统加载时频率特征，节点5在0.5s时负荷突增系统频率响应如图17所示，可知频率关于负荷突增仍然具有保序关系，不同负荷增载比例下的频率响应曲线保序。
[0178]
(2)西藏电网
[0179]
长期以来，西藏电网呈现电网容量小、负荷水平低、直流输电受限、光伏发电系统
等电力电子设备众多、有无功高度耦合等特点，电网长期存在安全稳定运行风险。为改善以上问题，藏中500kv联网工程于2018年建成，以长链式双回路与昌都电网相连，并通过芒康-巴塘与四川电网联网。若长链式通道故障断开，西藏电网将变为孤网运行，孤网的短路容量和调频调压能力与联网方式相比显著降低，在此种情况下，有必要采取紧急切负荷的控制措施。
[0180]
设置芒康-左贡线路在50周波时发生三相短路，5周波后n-2切除故障线路。仿真发现故障清除后，西藏电网频率不能恢复，并出现“二次跌落”的现象。
[0181]
紧急切载将有助于系统频率恢复稳定。选取频率最低节点附近负荷作为切载对象，仿真得到不同切载比例下藏中地区的频率变化曲线，如图18所示。可见，在大电网中切载过程仍然满足单调保序。
[0182]
上述记载论证了低频减载比率在传统电网以及含新能源电网中对系统频率的单调控制关系，为低频减载控制提供了理论依据。并且利用全状态模型，指出频率变化的影响因素包含机械功率、暂态电动势、功角以及输入量切载率，其中机械功率与输入量起决定性作用，表明频率稳定本质是有功平衡问题。但暂态电动势和功角对判定表达式的作用，说明了电力系统动态过程中功角、电压、频率是互相影响，相互耦合的。除此之外，利用灵敏度分析探究变量之间的相关性，对比相关参数变化趋势及变化大小，有助于指导电网故障时的参数控制，如由切载时机械功率与频率变化率灵敏度大，从而故障时可通过改变机械功率值使频率恢复期望值。
[0183]
对所公开的实施例的上述说明，使本领域专业技术人员能够实现或使用本发明。对这些实施例的多种修改对本领域的专业技术人员来说将是显而易见的，本文中所定义的一般原理可以在不脱离本发明的精神或范围的情况下，在其它实施例中实现。因此，本发明将不会被限制于本文所示的这些实施例，而是要符合与本文所公开的原理和新颖特点相一致的最宽的范围。