一种基于深度确定性策略梯度算法的配电网无功优化方法与流程

本发明涉及梯度算法配电网，特别是一种基于深度确定性策略梯度算法的配电网无功优化方法。

背景技术：

1、为了增加清洁和可持续能源在满足我们社会的电力需求中的份额，需要可再生资源的高渗透率，如太阳能光伏系统(photovoltaics，pv)。然而，由于这些资源输出功率的间歇性和波动性，必须解决电网可靠、优化和安全运行的技术挑战。在pv高渗透率的情况下，电压波动及其对系统有功功率损耗的影响是这些新的挑战之一。传统上，开关式或固定式电容器和有载分接开关变压器常被用于配电网的电压无功优化(volt/var optimization，vvo)，以保持网络中适当的电压水平。尽管这些传统设备对电压调节很有效，但它们的行动可能需要与快速反应的资源相协调，如pv或电池逆变器，特别是在光伏发电的高渗透率水平下。

2、vvo框架大致分为以下两种不同的方法：1)基于模型的优化方法，包括经典和启发式方法；2)基于学习的方法，如强化学习。混合整数线性规划和混合整数非线性规划是经典的优化方法之一，被广泛用于配电网的vvo。随机规划方法是对混合整数线性规划和混合整数非线性规划方法的补充，通过从一组可能的结果中纳入可能的情况来处理分布式能源资源和负荷需求的不确定性。在现实世界的应用中，这些方法可能面临着准确覆盖大范围不确定性的挑战。鲁邦优化方法最近得到了更多的关注，因为它们提高了优化解决方案对不同不确定性或不确定性集合的鲁邦性。然而，在所有这些方法中，由于存在与电压有关的负载模型和网络三相模型中各相之间的相互阻抗，计算上的挑战可能是巨大的。不同的启发式优化方法，如粒子群优化、蚁群优化、遗传算法已经被提出用于配电网的vvo，特别是用于具有完整非线性网络模型的非凸优化问题。尽管这些方法对复杂的场景和大数据集很有用，但它们对极度变化的条件并不稳健。这些方法的一个共同假设是认为网络拓扑结构和参数是高度精确的，这有时很难保证。此外，如果pv的输出功率在短时间内有较大的波动(超出预定的解决方案)，这些方法也不能提供准确的结果。

3、上述基于物理模型的方法高度依赖分析性优化算法，每当遇到新情况就必须解决，而且它们也无法迅速适应配电网中与时间有关的负荷和pv的变化。基于机器学习的模型已经被用来解决基于模型的方法的局限性，因为学习方法可以通过从历史数据中提取知识来处理不确定性。此外，基于机器学习的模型在遇到任何新情况时都不需要解决，因为它们可以使用从历史数据中获得的知识来解决这些问题。其中，基于深度强化学习(deepreinforcementlearning,drl)的方法被认为是基于模型的方法的有价值的替代方法，因为它们在神经网络中对非线性高维搜索空间具有强大的探索能力。基于drl的方法在本质上是无模型的，也就是说，它可以在不明确了解基础模型的情况下做出适当的决定。它减少了复杂问题的计算量，并能捕捉系统的硬模型动态。此外，drl方法在负荷或光伏曲线急剧变化的不确定环境中表现得比经典方法更好。

技术实现思路

1、本部分的目的在于概述本发明的实施例的一些方面以及简要介绍一些较佳实施例。在本部分以及本技术的说明书摘要和发明名称中可能会做些简化或省略以避免使本部分、说明书摘要和发明名称的目的模糊，而这种简化或省略不能用于限制本发明的范围。

2、鉴于上述和/或现有的一种基于深度确定性策略梯度算法的配电网无功优化方法中存在的问题，提出了本发明。

3、因此，本发明所要解决的问题在于如何提供一种基于深度确定性策略梯度算法的配电网无功优化方法，可以协调多个pv和电池储能系统的连续无功功率输出，并根据负载需求对bess进行充电和放电，以此来优化配电网的电压和降低有功损耗。

4、为解决上述技术问题，本发明提供如下技术方案：一种基于深度确定性策略梯度算法的配电网无功优化方法，其包括，

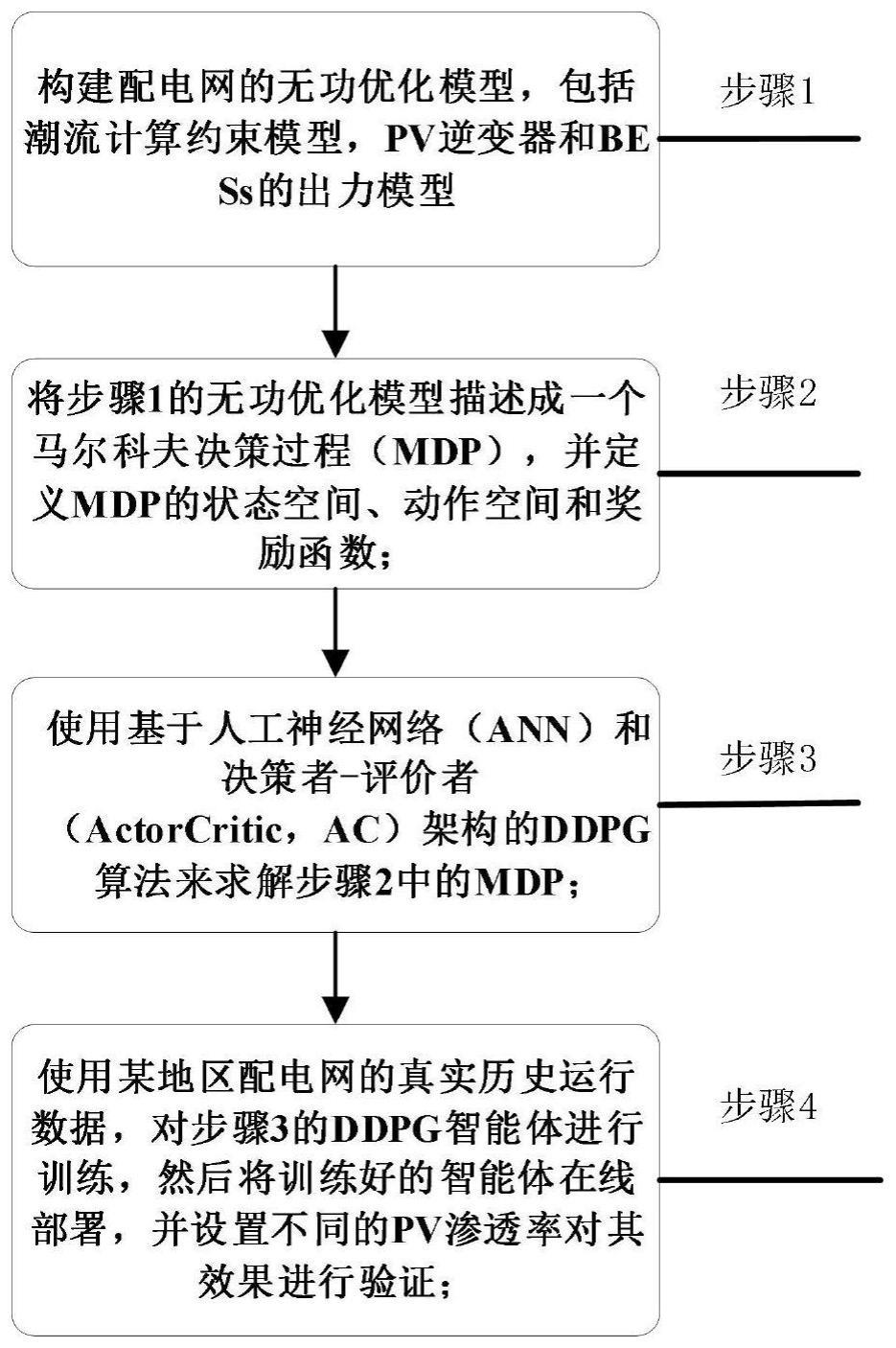
5、构建配电网的无功优化模型，包括潮流计算约束模型，pv逆变器和bess的出力模型；

6、将无功优化模型描述成一个马尔科夫决策过程，并定义mdp的状态空间、动作空间和奖励函数；

7、使用基于人工神经网络和决策者－评价者架构的ddpg算法来求解的mdp；

8、使用某地区配电网的真实历史运行数据，对ddpg智能体进行训练，然后将训练好的智能体在线部署，并设置不同的pv渗透率对其效果进行验证。

9、作为本发明所述一种基于深度确定性策略梯度算法的配电网无功优化方法的一种优选方案，其中：所述无功优化模型建立是

10、构建配电网的无功优化模型，包括潮流计算约束模型，pv逆变器和bess的出力模型，在无功优化模型中，目标函数是最小化配电网的有功损耗和电压偏差，约束条件是潮流计算过程中的功率平衡约束和节点电压约束，决策变量是pv逆变器和bess的出力，下式展示了配电网无功优化的数学模型：

11、min∑(ploss+|v-ve|)

12、此公式为无功优化的目标函数，ploss为配电系统的有功损耗，v表示节点电压，ve表示节点的额定电压；

13、

14、此公式为功率平衡约束，式中，n为配电网的节点总数，gij和bij分别表示节点导纳的实部和虚部，vi和vj为节点电压幅值，δi和δj表示节点电压的相角差；

15、vmin≤vi≤vmax

16、此公式为节点电压约束，式中，vmin和vmax分别为节点电压的上下限，该限制也被用于后面辅助奖励函数的惩罚项；

17、qpv.min≤qpv,i≤qpv.max

18、(ppv,i)2+(qpv,i)2≤(spv,i)2

19、上述公式分别为pv的有功无功出力约束，q为pv的有功无功出力约束，qpv,i表示i节点pv的无功输出量；表示i节点pv的无功输出量；

20、|qbes,i|≤qbes,max

21、上述公式为电池储能系统的无功出力约束，qbes,i表示i节点bes的无功输出量。

22、作为本发明所述一种基于深度确定性策略梯度算法的配电网无功优化方法的一种优选方案，其中：所述将无功优化模型描述成一个马尔科夫决策过程中定义mdp的状态空间、动作空间和奖励函数，ddpg智能体的目的是在分布式资源之间进行协调以提供快速有效的行动，同时根据观测的状态信息对分布式资源的动作进行管理，以调节配电网的电压和电力损耗，智能体的奖励函数的定义如下：

23、奖励函数：为了让智能体学习到最佳的策略，本发明根据最小化电压偏差和有功功率损耗两个目的，在奖励函数中考虑了两个约束，奖励函数定义如下：

24、rt＝-mp×(ploss(t)-p0)+mv

25、上式中r代表t时刻的奖励值，ploss(t)表示t时刻的配电网采取当前动作的有功损耗，p0表示在时刻t采取默认动作带来的有功损耗，mp和mv分别是有功损耗最小化和减小电压偏差的奖励，mp取值为7，如果没有电压违规，即系统节点的最低电压和最高电压处于正常区域(0.95-1.05)之间，mv为30，如果系统节点电压vmax＞1.05或者vmin＜0.95，mv为-10；

26、所述mdp就是马尔科夫决策过程。

27、作为本发明所述一种基于深度确定性策略梯度算法的配电网无功优化方法的一种优选方案，其中：所述利用算法求解mdp流程是

28、使用基于人工神经网络和决策者-评价者架构的ddpg算法来求解mdp，基于确定性策略的动作价值函数的贝尔曼方程递推关系如下：

29、qμ(st,at)＝e[r(st,at)+γqμ(st+1,μ(st+1))]

30、式中，μ(st+1)为确定性策略函数，ddpg算法使用actor神经网络来拟合μ(st+1)，st+1为t+1时刻的状态，qμ(st,at)表示动作价值函数，st和at表示t时刻的状态和动作，r(st,at)表示奖励函数，e表示期望，γ为折扣因子。

31、作为本发明所述一种基于深度确定性策略梯度算法的配电网无功优化方法的一种优选方案，其中：ddpg算法采用ac网络的架构，通过训练参数化的确定性策略μ(s,|θμ)深度神经网络来拟合策略优化过程，策略网络参数更新方式为：

32、

33、式中，θμ为actor网络的参数，代表梯度求解，e表示期望，同时ddpg算法考虑参数为θq的深度神经网critic来拟合状态价值函数。

34、作为本发明所述一种基于深度确定性策略梯度算法的配电网无功优化方法的一种优选方案，其中：所述验证部分使用某地区配电网的真实历史运行数据，对ddpg智能体进行训练，然后将训练好的智能体在线部署，并设置不同的pv渗透率对其效果进行验证，智能体和环境的交互过程，该过程会产生大量的历史经验，然后存入经验池中，当经验池的经验达到一定数量时，从中取样对智能体进行训练，智能体的训练过程就是critic和actor网络参数的更新过程，智能体训练完成后即可部署到环境中在线执行。

35、作为本发明所述一种基于深度确定性策略梯度算法的配电网无功优化方法的一种优选方案，其中：智能体的状态空间与动作空间的定义是：

36、状态空间：状态s表示配电网仿真环境运行的状态的测量向量，在本发明的问题中，将光伏逆变器的有功功率、配电网的功率损耗和节点电压作为状态输入，

37、动作空间：动作a被定义为不同控制变量的矢量，代表配电网中可控设备的动作量，本发明的动作为pv逆变器和bess的无功功率输出量，在每个决策步，pv逆变器和bess会通过改变自己的无功功率来保持电压水平极限和减少功率损耗。

38、作为本发明所述一种基于深度确定性策略梯度算法的配电网无功优化方法的一种优选方案，其中：最小化函数训练参数方式为

39、并通过最小化损失函数来训练参数：

40、l(θq)＝e[(q(st,at|θq)-yt)2]

41、yt＝r(st,at)+γq(st+1,μ(st+1)|θμ)

42、上式θq为critic网络的参数，e表示期望，γ为折扣因子，yt为t时刻的目标价值，该值由目标网络提供，可以看出，actor网络的参数的更新依赖于critic网络传递的策略梯度，若通过梯度更新之后神经网络用来拟合标签函数，会造成神经网络迭代更新产生发散，为了维持目标神经网络的稳定目标网络的参数更新采取软更新方式：

43、θ’←τθ+(1-τ)θ’

44、式中，θ'为目标网络的参数，τ为软更新系数，在ddpg算法中我们分别为actor和critic网络设置一个目标网络，这意味着目标网络参数在价值网络参数的约束下缓慢更新，这样价值网络更新过程便会拥有一个稳定的目标值，这样可以减少价值网络和策略网络之间的分歧，学习的稳定性大大提高。

45、一种计算机设备，包括存储器和处理器，所述存储器存储有计算机程序，其特征在于，所述处理器执行所述计算机程序时实现如上所述方法的步骤。

46、一种计算机可读存储介质，其上存储有计算机程序，其特征在于，所述计算机程序被处理器执行时实现如上所述方法的步骤。

47、本发明有益效果为

48、相比传统优化方法，本发明的drl方法可以在历史经验中捕获系统的不确定性，在每个决策步，训练好的强化学习智能体无需再对新的情况进行设计和求解，它可以根据当前的状态实时做出决策；相比现存基于q表的强化学习方法，本发明所提方法基于ann使用q网络来逼近q函数，避免了状态和动作的维度灾害，同时本发明可以很好地利用pv和bess这些分布式资源来进行配电网优化。