一种基于节点导纳矩阵的多目标最优碳流计算方法

本发明属于电力系统领域，特别涉及一种基于节点导纳矩阵的多目标最优碳流计算方法。

背景技术：

1、随着温室效益的不断增强，全球气候逐渐变暖，对环境造成了巨大的影响，对经济造成了严重的损失。我国作为全球碳排放量最多的国家之一，应该肩负起降碳的责任。因此，合理调度电力系统的机组出力，最大限度的降低碳排放，对于实现“双碳”目标具有举足轻重的现实意义。

2、碳流是一种依附于潮流的一种虚拟流，用于表征二氧化碳在某一时间段内从一个地点或系统流向另一个地点或系统的总量。碳流率是指从特定机组通过电网的支路与节点到达负荷的单位时间内的碳流量，用以表征短时间段内的碳排放量。目前的最优碳流是在经过潮流计算后，利用潮流分布矩阵按照比例分配的原则，进行碳排放的分摊，求取总电网的碳排放的最优值，但并未考虑新能源接入的影响。

技术实现思路

1、本发明的目的，在于提供一种基于节点导纳矩阵的多目标最优碳流计算方法，综合考虑风电机组和光伏机组的出力，实现电力系统的经济效益和节能减排。

2、为了达成上述目的，本发明的解决方案是：

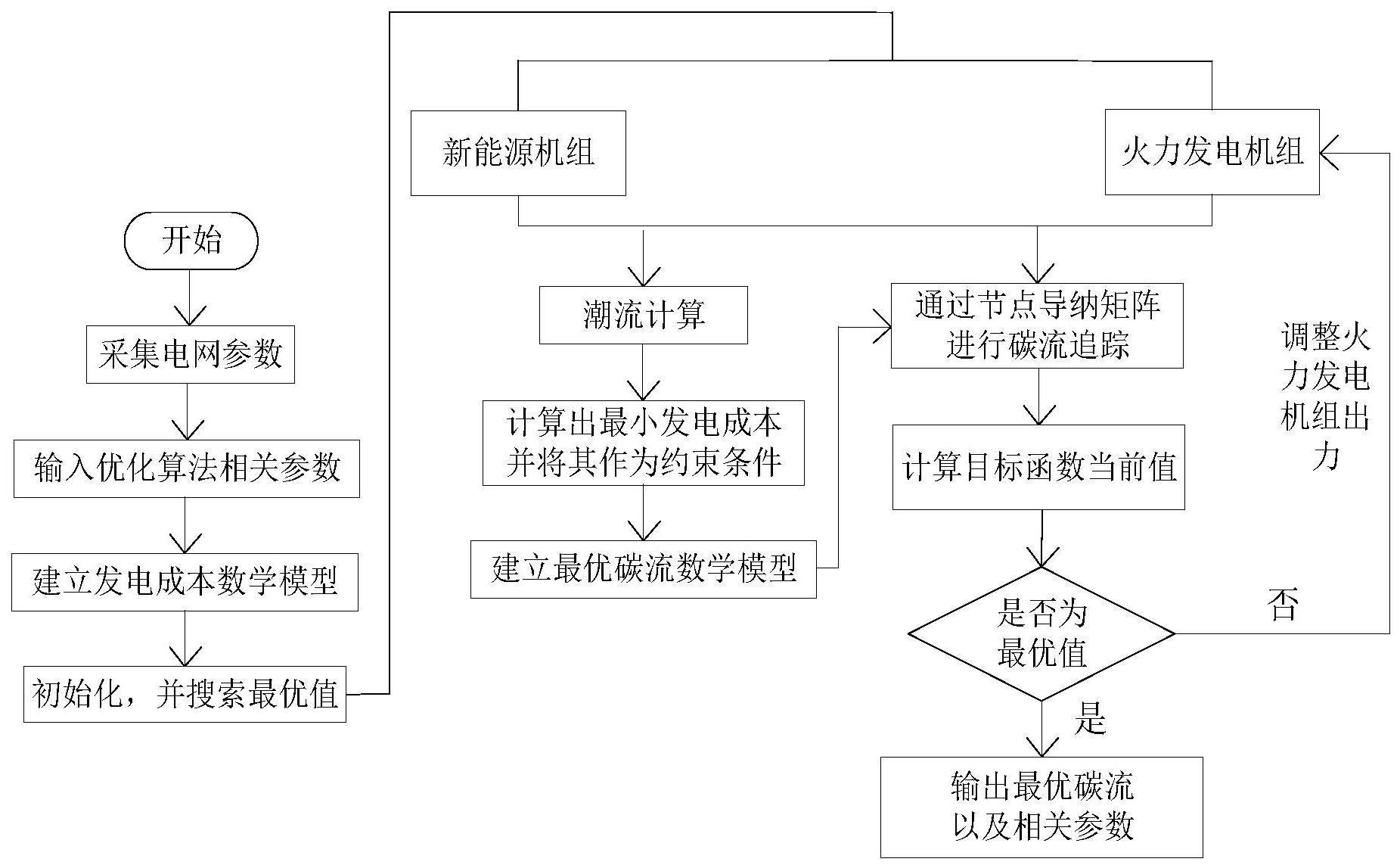
3、一种基于节点导纳矩阵的多目标最优碳流计算方法，包括如下步骤：

4、步骤1，采集电网数据，建立光伏机组的时变功率差模型和风电机组数学模型，通过初始化火力发电机组的出力，进行潮流计算，得到电网运行参数，确定电网运行状态；

5、步骤2，建立系统决策变量约束、系统状态变量约束和火电机组的爬坡约束；对步骤1潮流计算结果进行约束，得到约束后的潮流计算结果；

6、步骤3，根据步骤2约束后的潮流计算结果，建立电网发电成本函数；

7、步骤4，建立碳流计算数学模型，通过节点导纳矩阵计算负荷节点和支路网损分别分摊的发电机组产生的碳排放，量化光伏机组以及风电机组对火电机组碳排放的降低贡献；

8、步骤5，通过优化算法优化电网发电成本函数，计算发电成本最优值，并将其作为参考值，建立约束模型；通过节点导纳矩阵建立碳流率与火电机组出力的映射关系，建立最优碳流数学模型，通过优化算法确定最优碳流以及相关控制参数。

9、上述步骤1中，采集的电网数据是在潮流计算中需要应用到的数据，包括但不限于发电机组的输出功率pgi、电压幅值vgi、支路导纳、负荷功率pli和变压器变比nb，其中支路导纳包括支路电阻r、电抗x、电导g和对地导纳b；电网运行参数包括母线上的电压幅值、相角、有功功率和无功功率。

10、上述步骤1中，建立光伏机组的时变功率差模型的具体过程是：

11、建立光伏出力实际模型，公式如下所示：

12、p＝p0*i*[1+α(t-t0)]

13、其中，p为光伏阵列的输出功率，p0为标准测试条件下的额定功率，i为光照强度，α为光伏阵列的温度系数，t为光伏阵列的温度，t0为标准测试条件下的光伏阵列温度；

14、采用前向差分的方式对光伏出力实际模型进行离散化，公式如下所示：

15、p(k)＝p(k-1)+δ*km

16、其中，p(k)为第k个时刻的光伏阵列输出功率，δ为时间步长，km为第k-1个时刻到k时刻的功率变化率；

17、将光伏出力实际模型代入差分形式中，建立光伏机组的时变功率差模型，公式如下所示：

18、p(k)＝p(k-1)+δ*[p0*i(k-1)*α(t(k-1)-t0)]

19、其中，i(k-1)为k-1时刻的光照强度，t(k-1)为k-1时刻的光伏阵列的温度。

20、上述步骤1中，建立风电机组数学模型的具体过程是：

21、建立风力发电出力数学模型，公式如下所示：

22、

23、其中，

24、

25、

26、pw(v)代表单台发电机功率，v表示t时刻的风速，v1表示切入风速，v2表示切断风速，v0表示额定风速；

27、给定风电机组的额定功率pw0，即t时刻的pw，设定风电机组的初始电压为uw0；

28、基于风电机组的额定功率pw0和风电机组的初始电压为uw0，计算风电机组的滑差sw，公式如下所示：

29、

30、其中，xk＝x1+x2，r2为转子电阻，x1和x2分别为定子电抗和转子电抗；

31、基于风电机组的额定功率pw0和风电机组的滑差sw计算风电机组的无功功率qw，公式如下所示：

32、

33、将风电机组视为pq节点，进行潮流计算，得到风电机组的节点电压更新值uw；

34、若uw≠uw0，则令重复计算风电机组的滑差sw、风电机组的无功功率qw和风电机组的节点电压更新值uw，直至|uw-uw0|＜ε，其中，ε＝1×10-5。

35、上述步骤2中，系统决策变量为除平衡节点、光伏机组和风电机组以外的所有火电机组的出力，约束条件为其中和为所述系统决策变量的下限和上限；

36、系统状态变量x是指所有母线的有功功率、无功功率和电压幅值与所有支路的有功功率和无功功率，即x(p1，q1，vg，pij，qij)，约束条件为xmin＜x＜xmax，其中xmin和xmax为所述系统状态变量的下限和上限；

37、火电机组的爬坡约束z是指其中和pigup分别为第i台火电机组的最大向下爬坡功率和最大向上爬坡功率。

38、上述步骤3中，建立火电机组的发电成本公式如下所示：

39、

40、

41、

42、其中，表示第t时刻火电机组的成本，表示t时刻第i台火电机组的发电功率，表示第i台火电机组的运行成本，ai、bi、ci分别为运行成本的二次项、一次项和常数项成本系数；cgi为第t台机组启停成本和损耗成本之和；

43、建立光伏机组的发电成本公式如下所示：

44、

45、

46、其中，为第i台t时刻的光伏机组发电成本，cpv为光伏机组发点成本系数，表示第i台t时刻的光伏机组发电功率，n1表示光伏机组的个数；

47、建立风电机组的发电成本公式如下所示：

48、

49、

50、其中，为第i台t时刻的光伏机组发电成本，cwd为风电机组发点成本系数，表示第i台t时刻的风电机组发电功率，n2表示风电机组的个数；

51、建立电网发电成本函数call，公式如下所示：

52、

53、上述步骤4中，进行潮流计算，得到节点导纳矩阵y、发电机流入电流igi和负荷流出电流ilo，可知：igi-ilo＝yu；其中，u为母线电压；

54、定义五种等效导纳矩阵：发电机等效导纳矩阵yg、负荷等效导纳矩阵yl、节点等效电纳矩阵yc、节点母线并联导纳yx、线路导纳矩阵yb，根据ic＝ycu、ix＝yxu、ib＝ybu计算出节点等效电纳导致的节点流入电流ic、节点母线并联导纳导致的节点流出电流ix和线路电流ib；

55、通过五种等效导纳矩阵进行潮流追踪，将所有发电机组的出力分配给所有负荷节点的功率和支路的功率，依据发电机组的类型，确定碳排放强度eg，通过碳流追踪，将发电机组产生的碳排放分摊给负荷节点碳流率el和支路网损碳流率eq，公式如下所示：

56、el(g，l)＝eg(g，g)·re[sgi(g，l)]

57、

58、其中，eg＝diag(eg)，sgi(g，l)表示第g个发电机组分配给第l个负荷的功率，如果k节点不存在负荷，则sgi(g，k)＝0，表示第g个发电机组向线路q分配的首段功率，表示第q个发电机组向线路g分配的末段功率。

59、上述步骤4中，第i台光伏机组对于第j个火电机组贡献的碳流率的公式如下所示：

60、

61、g(i，j)＝yg(yg-yn+yx)-1

62、其中，表示第i台光伏机组对于第j个火电机组分配的碳流率，ud表示节点电压对角化，表示第j个火电机组的输入功率；

63、第i台风电机组对于第j个火电机组贡献的碳流率为：

64、

65、其中，第i台光伏机组对第j个火电机组分配的碳流率，表示第j个风电机组的输入功率。

66、上述步骤5中，以火电机组出力作为系统决策变量，步骤2中的约束、火电机组的爬坡约束z为边界条件，优化电网发电成本函数，公式如下所示：

67、

68、

69、其中，fmin为发电成本的优化函数，为约束条件；

70、通过优化算法计算出发电成本最优值为并将其作为约束条件y，公式如下所示：

71、

72、其中，∝表示成本系数；

73、上述步骤5中，通过节点导纳矩阵建立碳流率和除平衡节点以外的火电机组出力的关系，基于碳流追踪的结果可得目标函数的公式如下所示：

74、

75、其中，n为电网系统的节点个数，m为电网系统的支路个数；

76、将所有负荷节点与支路网损的碳流率之和作为目标函数，建立最优碳流数学模型，公式如下所示：

77、

78、s.t.cst(pg，x，y，z)≤0

79、其中，为最优碳流的目标函数，代表不等式约束；

80、采用群智能优化算法，求取的最佳适应度，得到目标函数的最优值，即最优碳流以及相关控制参数。

81、采用本发明提供的多目标最优碳流计算方法，能够在考虑光伏机组和风电机组出力的情况下，通过优化算法计算出最优碳流，实现电力系统的节能减排，增加经济效益。