一种考虑主动网络管理的配电网新能源消纳能力鲁棒评估方法与系统与流程

本发明涉及配电网新能源消纳能力评估，尤其涉及一种考虑主动网络管理的配电网新能源消纳能力鲁棒评估方法与系统。

背景技术：

1、分布式新能源作为应对能源危机和环境污染的一项极具前景的解决方案，近些年在配电网中的渗透率不断增加，但也给配电网的安全运行带来了电压超限、潮流逆送、电能质量下降等问题。为了解决这些问题，亟需对配电网的新能源消纳能力进行全面评估。然而由于新能源本身的随机波动性和传统配电网无法充分发挥“源网荷储”的主动调节能力，使得现有方法评估结果误差较大，因此需要我们提出一种新的评估方法，充分考虑这些客观因素，从而准确评估配电网的消纳能力。

2、主动网络管理技术(anm)主要包括网络重构、无功补偿调节、电压调节控制、分布式发电功率因素控制等手段，可以通过重新调度配电网拓扑结构和调整注入功率等手段，有效提高配电网的新能源消纳能力。然而现有的研究都对主动管理技术考虑不够充分，无法充分利用“源网荷储”的能动性来合理评估配电网的新能源消纳能力。

3、除此之外，分布式新能源固有的随机波动性也给配电网消纳能力的准确评估带来很大困难。从长期来看，配电网分布式新能源出力目前仍然无法准确预测。而现有配电网的实时测量数据也十分有限，这进一步加剧了分布式新能源出力的预测误差，给消纳能力的合理评估带来了极大困难。在目前一部分研究中，通过使用基于场景生成的随机优化，可以使模型与确定性模型保持一致，但是在实际中很难获得这些不确定性变量的真实概率分布，并且加入大量的场景也会给消纳能力评估计算带来很大的困难。而作为解决新能源随机波动性的另一种有效方法，鲁棒优化(ro)不需要不确定变量的真实概率分布，且两阶段的鲁棒优化算法能够很好地在可行性和保守性之间取得平衡，能够很好地对配电网的新能源消纳能力做出准确评估。近年来，鲁棒优化已经被广泛用于机组组合(uc)、电力系统规划、最优潮流等电力系统问题。

4、综上所述，目前的研究没有合理地运用和处理主动网络管理技术和对新能源随机波动性的影响，从而无法对配电网的新能源消纳能力进行准确评估。针对这些问题，本文基于两阶段鲁棒优化方法来应对新能源的随机波动性，并通过网络重构、无功补偿和有载电压调节等主动网络管理技术充分运用“源网荷储”的能动性，建立了配电网新能源消纳能力的鲁棒评估方法。该模型构建了新能源/负荷多面体的不确定模型，并以最坏实现场景指导模型第一阶段的配电网节点新能源最大消纳能力决策；模型第二阶段考虑配电网主动网络管理技术，以第一阶段评估结果为基础，决策最坏场景下的配电网运行策略。然后，本文提出模型线性化方法，并采用列和约束生成算法对上述两阶段鲁棒模型分解为单层线性模型进行迭代求解。

技术实现思路

1、符号及定义：

2、a.指数、集合和矩阵：

3、 t，i，ij 时间、节点、输电线路索引 <![cdata[n_dg，n_nr]]> 接入分布式新能源的节点集合、除根节点以外的节点集合 n(i) 与节点i直接相连的所有节点的集合、 λ，γ 对偶变量和松弛变量的向量 <![cdata[g₁-g₅，]]> 系数矩阵 a，b，b，g，d 系数矩阵 k 算法迭代索引

4、b.变量

5、

6、c.常量

7、

8、

9、d.缩写

10、 anm 主动网络管理技术 opf 最优潮流 so 随机优化 ro 鲁棒优化 oltc 有载调压变压器 svc 无功补偿装置 dc-cam 确定性配电网最大消纳模型 rc-cam 配电网消纳评估鲁棒模型 lp，milp 线性规划、混合整数线性规划 ccg 列和约束生成算法

11、本发明的目的在于提供一种考虑主动网络管理的配电网新能源消纳能力鲁棒评估方法与系统。该方法提出了一种新的配电网新能源消纳能力评估方法，基于主动网络管理技术构建了新型配电网运行模型，并运用两阶段鲁棒优化算法来处理评估过程中分布式新能源和用户负荷需求的波动性。通过使用列和约束生成(ccg)方法，从原始的两阶段鲁棒评估模型中获得混合整数的主问题，和非凸max-min子问题。主问题以最坏场景指导得到配电网节点新能源最大承纳能力决策；子问题再以主问题的决策为基础，决策最坏场景下的配电网运行策略，并将该场景纳入到主问题中，该方法在抵御新能源/负荷需求随机波动性和实现配电网消纳能力评估最优解方面具有优越性。

12、为实现上述目的，本发明提供了一种考虑主动网络管理的配电网新能源消纳能力鲁棒评估方法与系统，其特征在于：基于一种主动网络技术和两阶段鲁棒优化算法，步骤如下：

13、s1、建立考虑主动网络管理技术的新能源消纳能力评估模型；

14、s2、实现消纳能力评估模型的线性化，建立新能源和负荷需求的多面体不确定性模型；

15、s3、将评估模型构建为为两阶段鲁棒优化的形式，并运用列和约束生成算法生成主问题和子问题分别求解。

16、优选的，分布式新能源消纳能力的确定性评估模型：

17、(1)目标函数

18、为了准确评估配电网的新能源消纳能力，本文以配电网每个可装机节点的最大新能源机组装机量之和为目标函数，如式(1)所示。

19、

20、其中i为配电网的节点；ndg表示配电网中能够接入分布式新能源的节点集合；yi表示配电网每个节点的分布式新能源装机量。

21、(2)配电网拓扑约束

22、由于配电网具有独特的拓扑约束，因此通过约束配电网节点和线路的数量关系，可以保证在配电网进行网络重构后仍能保持辐射状结构，如式式(2)所示。通过给定每个节点增加一个虚拟单位负荷和虚拟潮流变量ρij,t，保证网络重构后配电网的潮流约束，如式(3)所示。

23、

24、

25、其中，ij表示配电网的线路；wij,t为在时刻t时线路ij的通断状态变量；nb和nroot分别表示配电网节点总数和根节点的数量；dij∈{-1,1}表示线路ij的潮流方向参数；n(i)表示与节点i直接相连的所有节点的集合；nnr表示除根节点以外的节点集合；ρij,t表示线路ij的非负虚拟潮流变量。

26、(3)分布式新能源出力约束

27、考虑到分布式新能源的充分利用，本文假定其有功输出在最大功率跟踪模式下运行，而无功输出可在预定范围内连续调节，如式(4)和(5)所示。

28、

29、

30、其中，为节点i的分布式新能源预测出力系数；和分别为节点i的分布式新能源的有功和无功出力；θi,min和θi,max分别为功率因数角的最大最小值。

31、(4)无功补偿装置输出约束

32、由于配电网中包含连续调节无功补偿装置和离散调节无功补偿装置两种无功补偿器，其无功补偿功率建模分别如式(6)和(7)所示。

33、

34、

35、其中，为连续调节无功补偿装置的无功注入；和分别表示连续调节无功补偿无功功率的上下限；为离散调节无功补偿装置的无功注入；χi,t和χi,max分别表示离散调节无功补偿装置的调节档位和其上限。

36、(5)配电网潮流约束

37、a)节点潮流约束

38、考虑到配电网中接入大量负荷以及线路高阻抗，其运行造成的网络损耗不容忽视，因此建立包含线路损耗的二阶锥潮流约束，如式(8)所示。

39、

40、其中，pij,t和qij,t为线路的有功和无功潮流；和为节点i的负荷需求预测值，iij为线路ij的电流幅值平方。

41、b)线路压降约束

42、对于没有变压器的线路来说，线路压降约束为：

43、

44、其中，ui,t和uj,t分别表示线路两端电压的平方值；rij和xij分别表示配电网线路的自电阻和自电抗。在式(9)中并没有体现anm技术的网络重构策略，因此我们修改模型来将网络重构策略加入到模型中，如式(10)所示。

45、

46、对于有变压器的线路来说，线路压降约束为：

47、

48、其中，um,t为节点电压uj,t经过有载调压变压器(oltc)调节的电压平方值；τij,t和为有载调压变压器的变比及其最小值；tij,t为一个非负整数，表示oltc实际的分接档位；kij为oltc总的档位数；δτij表示每个分接档位的单位变比。

49、(6)线路容量约束

50、考虑到需保证配电网的安全运行，因此对其线路容量进行约束，如式(12)所示。

51、

52、其中，sij,max为配电网线路容量。在式(19)中加入wij,t来将未并网的线路中的潮流限制为0。

53、(7)节点电压约束

54、考虑到需保证配电网的安全运行，因此对其节点电压进行上下限约束，如式(13)所示。

55、ui,min≤ui,t≤ui,max  (13)

56、其中，ui,max和ui,min分别表示节点电压平方值的上下限。

57、综上所述，我们建立起了评估和提升确定性参数的配电网最大消纳能力的模型(dc-cam)，它是一个混合整数线性规划(milp)，如式(14)所示。

58、

59、然而，在dc-cam模型当中，将负荷有功、无功需求以及分布式新能源出力的能效系数预测值作为确定性参数输入是不合理的。忽略了实际运行中的显著不确定性因素会导致最终的评估结果和安装策略误差过大，为了保证模型的真实性和可行性，因此需要建立考虑显著不确定性因素的最大分布式新能源承载能力评估模型。

60、优选的，模型线性化方法及不确定性模型构建：

61、(1)配电网拓扑约束线性化

62、可以看出，式(3)中wij,t·ρij,t为两个变量相乘的非线性项，令θij,t＝wij,t·ρij,t，并将其进行线性化处理，如式(15)所示。

63、

64、其中，m0为一个很大的正数。

65、(2)无功补偿装置输出约束线性化

66、易观察到式(7)中χi,t为离散变量，易增加模型求解难度，因此，通过引入布尔变量将其重新表述为二进制展开形式，如式(16)所示。

67、

68、其中，为χi,t二进制展开后每一位的数值；mi表示二进制表达式的长度。经过转换，该约束中的离散变量转换为了一系列的布尔变量，降低了求解难度。

69、(3)线路压降约束线性化

70、显然，式(11)中存在离散变量，且存在高次项，易造成模型求解困难，因此需将其进行相应的线性化处理。

71、a)将tij,t表示为如式(17)所示的二进制表达式。

72、

73、其中，为tij,t二进制展开后每一位的数值，它是一个布尔变量；nij为kij的二进制位数。

74、b)设中间变量μij,t＝τij,t·uj,t，并将其进行变换。

75、

76、令并将其线性化可得：

77、

78、c)令um,t＝τij,t·μij,t，并将其转换可得um,t的最终表达式。

79、

80、令并将其线性化可得：

81、

82、(4)线路容量约束线性化

83、观察到式(12)具有较多二次项，造成模型求解困难，可以用式(22)近似代替。

84、

85、(5)不确定性模型建立

86、根据历史数据的分布情况，分别建立分布式新能源出力能效系数和负荷需求的盒式不确定集合，如式(23)所示。

87、

88、其中，分别为分布式新能源出力能效系数和负荷需求的实际值；δηi,t，δpi,t，分别为它们的上下限波动范围。

89、式(23)可以进一步转换为具有归一化波动误差的形式，如式(24)所示。

90、

91、

92、模型建立的不确定性集合可以通过调节bt来调节鲁棒优化模型的保守度，从而得到需要的策略。

93、优选的，鲁棒模型及其ccg求解算法：

94、(1)两阶段鲁棒模型构建

95、在对新能源和用户负荷需求不确定性进行建模后，本节通过添加恒正的松弛变量将潮流平衡公式(8)修改为式(26)，其中ε为安全越限值。最终建立两阶段鲁棒形式的rc-cam模型，如式(27)所示。

96、

97、

98、在内层模型中，从不确定性集合中寻找影响分布式新能源承载能力的最差场景，其中为优化变量。在得到最差场景后将其带入到外层模型中，得到满足多个场景的新能源机组安装和anm运行策略，以最大化配电网的分布式新能源的承载能力。

99、将rc-cam模型中所有的变量分为四种类型，其中包括分布式新能源机组rdg安装决策变量y，潮流分布向量z和a等连续向量，不确定向量u等布尔变量，详细映射关系如式(28)所示。

100、

101、由此，rc-cam的模型可以重新表述为紧凑形式，具体表示为式(29)-(32)。

102、

103、

104、

105、bu≤d  (32)

106、其中y、π和ω是相关变量的可行性集合。rc-cam中的其余约束条件由公式(31)表述，为了表述简洁，所有的等式约束都以等价的统一形式重新表示为不等式，其中a，g1-g5，b，b，g和d为相关约束对应的参数。

107、(2)主问题模型求解

108、对于rc-cam三层两阶段鲁棒优化模型，由于不确定集ω存在无穷多个场景导致模型存在有无穷多个变量和约束，常用的成熟求解器(如cplex，gurobi)已无法直接求解。本节将使用列和约束生成算法(ccg)，采用迭代的方式对模型进行求解。通过在主问题每次迭代过程中不断加入和子问题相关的变量和约束，可以有效降低迭代次数，保证模型求解的高效性和全局最优性。根据两阶段优化不同的目标，将rc-cam模型分解为以下主问题mp模型和子问题sp模型以降低模型规模。

109、mp模型紧凑形式如公式(33)所示，为线性优化模型(lp)。mp模型采用有限个场景子集uk取代不确定集合进行合理简化，并利用有限部分枚举场景来逼近不确定集合π，在某些给定的有限场景子集uk(由sp模型产生)下找到最佳的第一阶段决策y*。显然，mp模型其最优目标值在每次迭代中为rc-cam模型提供了一个下界，随着迭代次数的递增，最优目标值会逼近最优解。

110、

111、(3)子问题模型求解

112、sp模型的紧凑形式如公式(34)所示。本质上，sp模型是mp模型的可行性检验，由于mp模型是在有限个场景子集uk中优化决策变量y*，只满足在上述有限场景中决策是可行的。而原问题rc-cam模型是要求在最劣的场景下求得最佳决策变量，即最佳决策变量满足在所有场景uk(k∈k)下均可保证策略的可行性，因此mp模型和rc-cam并不等价。引入sp模型便很好地解决此问题，在每次迭代中为mp模型生成最坏场景，保证mp模型策略在所有场景下的可行性。

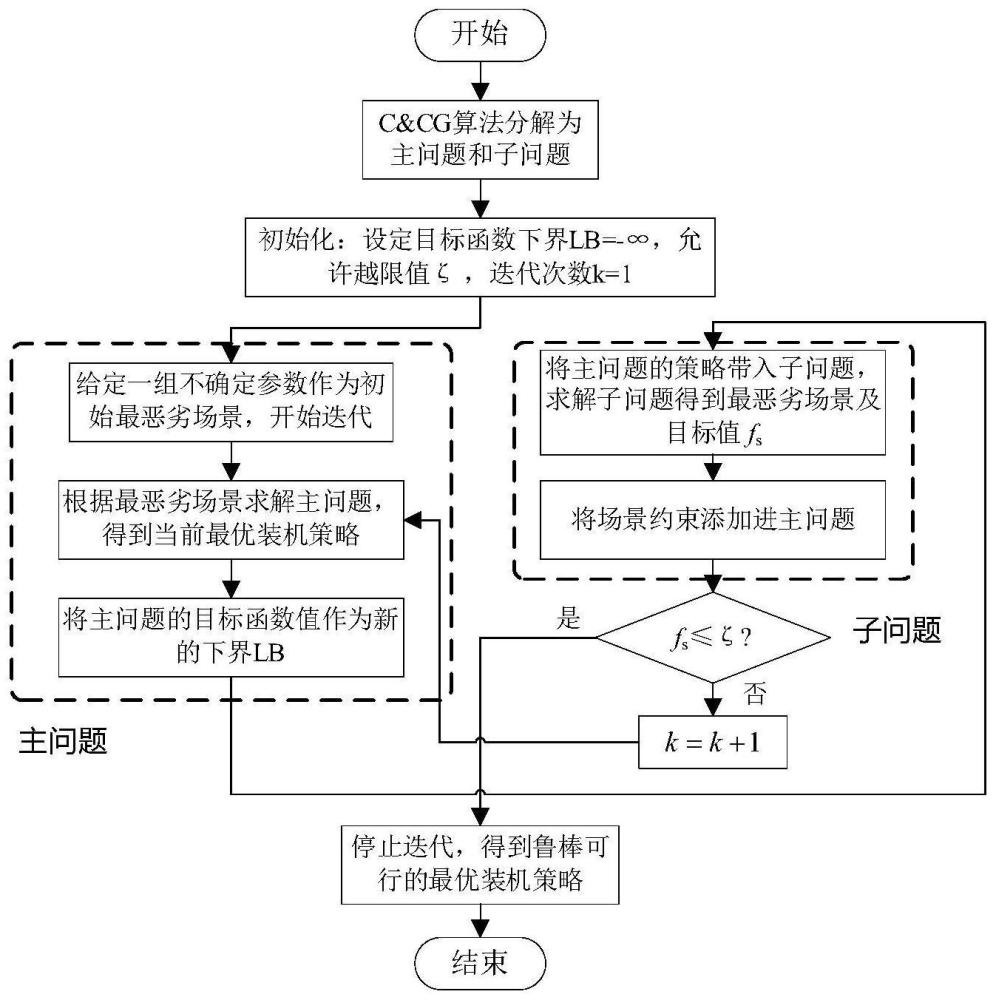
113、

114、显然，sp模型为max-min双层优化模型，为了求解方便，根据强对偶性原则，将内层min问题模型转化为max问题模型，简化后的双层优化模型如式(35)所示。

115、

116、式(35)中λ为相应约束的对偶变量，观察到上述模型目标函数式中存在双线性项ut·λ，为了求解简单，将不确定预算约束中u设为布尔变量，再利用大m法同时引入辅助变量γi＝ui·λi，将双线性项ut·λ等价转化为线性形式，模型转化为混合整数线性优化模型(milp)，如(36)所示。

117、

118、至此，mp模型、sp模型分别转换为lp和milp模型，可以采用成熟的商业求解器求解。

119、(4)列和约束生成算法

120、鲁棒优化的目标是基于不确定集合中的最劣场景求得最优值。mp模型主要提供当前迭代中的最优值y*，而sp模型主要提供当前mp模型策略下的最劣场景uk，因此可以通过列和约束生成算法(ccg)进行迭代求解，具体如表(1)所示。

121、表1列和约束生成算法(ccg)

122、