一种基于暂态电压稳定指标多项式逼近的暂态电压稳定预防控制方法与流程

本发明属于电力系统自动化领域，具体涉及一种基于暂态电压稳定指标多项式逼近的暂态电压稳定预防控制方法。

背景技术：

1、社会的正常运转和经济的发展都深刻地依赖于电力系统的安全稳定运行。随着人们对电力的不断增加的依赖，确保电力的可靠供应成为电力系统的至关重要的任务。在面临巨大挑战的今天，大规模的扰动可能导致电力系统的稳定性受到威胁，引发一系列严重后果，如连锁故障、直流闭锁故障、大停电等。回顾历史，2003年美国加州大停电是由于树枝引起的三相短路事故，而2012年印度7.30大停电则是由于电力供应不足和电网管理体制的滞后所致。此外，在荷兰、意大利等国家，也曾发生由系统失稳引发的大停电事故。这些灾难性的事件突显了加强暂态电压稳定预防控制等切实可行的控制措施的紧迫性和重要性。若系统潜藏暂态失稳的威胁，必须采用切实有效的控制手段以提升系统的稳定水平。对电力系统在巨大扰动降临之前进行控制的方法被称之为预防控制；而在扰动发生后，为了防止系统陷入失稳状态所采取的控制手段被称之为紧急控制。

2、暂态电压稳定预防控制作为电力系统暂态稳定的一个重要方面，长期以来备受广大学者的关注。随着长距离容量输电系统的不断扩大建成，暂态电压稳定问题日益显著。高压直流输电系统的受端依赖于外部系统输送的电力，而系统内无功储备不足。因此，对系统的暂态电压稳定问题予以关注显得尤为重要。对于瞬态电压稳定的评估，有多种方法可供选择，包括基于物理和数学原理的解析法、新兴的数据驱动方法以及瞬态电压指标法等。解析法可给出暂态电压稳定的机理分析，数据驱动法适用于大规模系统的暂态电压稳定评估，而指标法可给出系统的暂态电压稳定程度。

3、基于解析的预防控制方法，其暂态电压稳定约束的近似多项式通常较为复杂，导致模型规模较大，对于模型的求解会耗时较长。而基于数据驱动的预防控制方法相比，控制变量与一定tvsi之间的非线性关系无法用近似多项式表示，可解释性不强。

技术实现思路

1、本发明的目的在于解决上述技术问题，提供一种基于暂态电压稳定指标多项式逼近的暂态电压稳定预防控制方法，该方法将控制变量映射到特定tvsi的隐式函数，配点法的多项式逼近方法来逼近隐函数，具有较高的精度，并且基于近似多项式来构造暂态电压稳定约束，使得能采用内点法来求解初具nlp问题形式的预防控制模型，较快获得相应预防控制措施，从而达到维护电力系统安全稳定运行的目的。

2、为实现上述目的，本发明的技术方案是：一种基于暂态电压稳定指标多项式逼近的暂态电压稳定预防控制方法，包括如下步骤：

3、a、基于带预防控制变量的电力系统微分代数方程，通过建立多二进制表来把暂态电压轨迹的倾角划分为多个区域，对不同的区域赋予不同的权重，描述出暂态电压轨迹的倾角特征，定义出所有节点的tvsi隐式函数；

4、b、引入配点法，再采用多项式逼近方法对所求的tvsi隐式函数进行逼近，通过获得基函数和基函数的相应系数，获得tvsi隐式函数的对应近似多项式；

5、c、采用预选临界故障法来构造暂态电压的稳定约束，将预防控制模型转化为一个非线性规划问题，使得暂态电压稳定预防控制问题易于用内点法求解。

6、在本发明一实施例中，步骤a中，带预防控制变量的电力系统微分代数方程表示如下：

7、

8、式中，f为微分方程，g为代数方程，x为系统状态变量向量，y为系统代数变量向量，p为控制变量向量；每个p通过公式(1)定义一组x和y的轨迹，表示为隐式函数x(t；p)和y(t；p)，并定义暂态电压稳定指标i为x(t；p)和y(t；p)，i即p的隐式函数，记为i(p)。

9、如果得到i(p)的解析表达式，则可以直接从p的值计算出i，无需计算式(1)；另一方面，用i(p)表示的暂态电压稳定约束可以作为仅由p组成的方程(1)的替代模型，从而降低了预防控制模型的求解难度。

10、然而，隐函数i(p)的精确解析表达式是很难甚至不可能得到的。

11、在本发明一实施例中，将i(p)通过一个显式多项式来近似，记为～i(p)；根据多项式近似理论，表示为：

12、

13、式中φk(p)为第k个基函数，ck为φk(p)的系数，nb是基函数的个数。

14、在本发明一实施例中，步骤a中，通过建立多二进制表来把暂态电压轨迹的倾角划分为多个区域，对不同的区域赋予不同的权重，描述出暂态电压轨迹的倾角特征，定义出所有节点的tvsi隐式函数，具体如下：

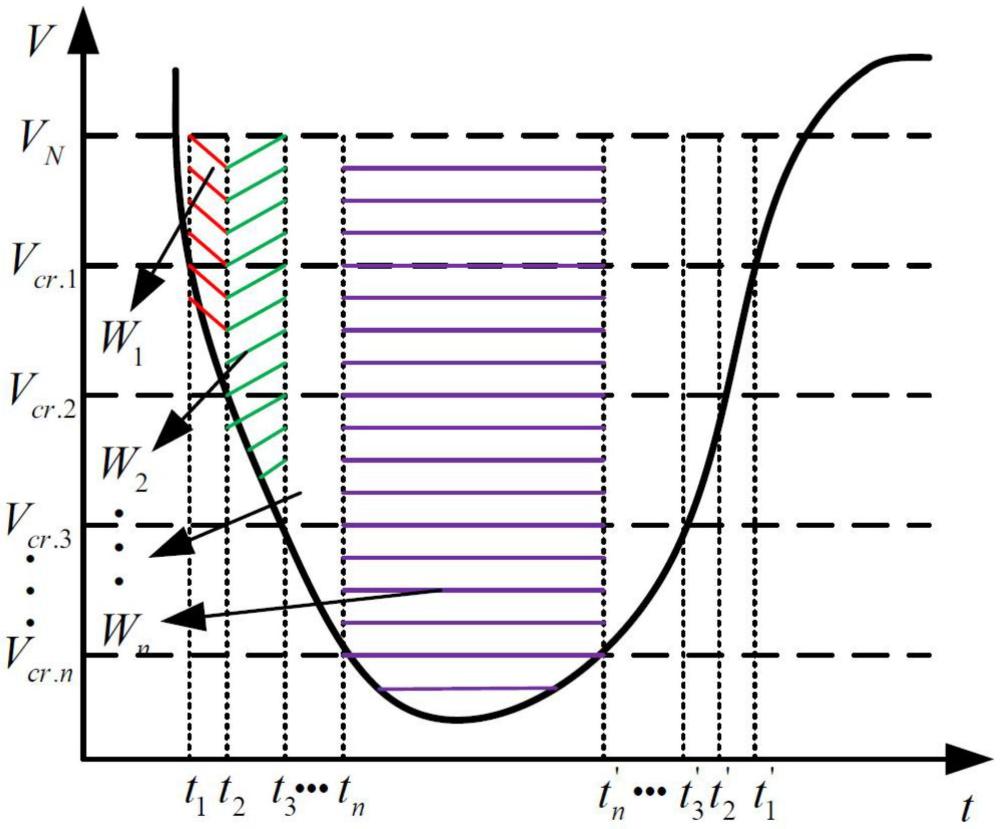
15、电压二进制值表(vcr,tcr)用来描述暂态电压轨迹在最大时间tcr低于阈值vcr时的下降；然而，基于单二元表的tvsi无法区分长时间小电压下降和短时间大电压下降的情况，不能很好地描述瞬态电压轨迹下降的特征。因此，采用如图1所示的多二进制表将暂态电压轨迹的倾角划分为多个区域。对不同的区域赋予不同的权重，可以很好地描述暂态电压轨迹的倾角特征。

16、图1为电压阈值vcr,i(1≤i≤n)对应的多二进制表，其中n为二进制表的个数；vn为基准电压；wi是分配给vcr,i和vcr,i+1之间区域的权值；ti为电压下降过程中电压轨迹进入区域的时刻，ti’为电压恢复过程中电压轨迹离开相应区域的时刻；基于多二进制表描述的电压轨迹倾角累积极限，定义tvsi隐式函数如下：

17、

18、式中ii为节点i的tvsi隐式函数；vi(t)是节点i在时刻t的电压；tj、tj+1和t′j+1、t′j分别为电压下降过程和恢复过程中电压轨迹进入和离开vcr,j和vcr,j+1之间区域的时刻；wj是分配给vcr,j和vcr,j+1之间区域的权值，其值通过下式求解，使ii＝0对应的暂态电压临界稳定；

19、

20、首先可以计算出所有关键节点的ii，并将其最小值定义为系统的i；其次，需要根据实际操作要求设计合适的多二进制表。在本发明中，根据(0.75p.u,1s)和(0.80p.u,10s)设计两个二进制表。

21、在本发明一实施例中，步骤b中，引入配点法，再采用多项式逼近方法对所求的tvsi隐式函数进行逼近，通过获得基函数和基函数的相应系数，获得tvsi隐式函数的对应近似多项式，具体如下：

22、本发明引入基于配点法的多项式逼近方法来逼近隐函数，其中与公式(2)相对应的i(p)的多项式逼近的两个基本问题是如何形成基函数φk(p)和如何计算基函数系数ck。

23、对于单个参数pi，如果认为pi在一个区间内，则其基函数φki(pi)(ki＝0,1,2，…)，其中ki为φki(pi)的度，多项式的递归表达式如下：

24、

25、对于d维参数向量p＝(p1,p2，…，pd)，每一个都在一个区间内，它的基函数φk(p)，其中k是φk(p)的序号，基函数φk(p)由φki(pi)(1≤i≤d)的乘积构成，即规定等于或小于近似阶l，因此，φk(p)的集合如下：

26、

27、式中表示张量积，nb＝(l+d)！/(l！d！)表示基函数个数；

28、根据多项式近似理论，使2-范数误差最小的基函数φk(p)的系数ck应为：

29、

30、式中<·，·>表示内积；虽然公式(7)的分子是对隐式函数i(p)的积分，很难解析得到其值，但可以用数值方法计算，具体公式如下：

31、

32、式中m是配点的个数；pm和bm表示第m个配点及其对应的积分系数；

33、配点pm(1≤m≤m)和积分系数bm的计算取决于具体的算法。将公式(6)形成的φk(p)和公式(8)计算的ck代入公式(2)，得到近似多项式

34、在本发明一实施例中，步骤c中，采用预选临界故障法来构造暂态电压的稳定约束，具体如下：

35、

36、式中d为控制变量的个数，即p的维数；ps,0和δps(1≤s≤d)分别为控制变量ps的初始值和控制量；暂态电压稳定约束公式(9)由一个简单的近似多项式表示，该近似多项式仅由控制变量p组成；因此，包含暂态电压稳定约束的预防控制模型能够表示为nlp问题。

37、在本发明一实施例中，步骤c中，将预防控制模型转化为一个非线性规划问题即nlp问题，具体如下：

38、预防控制模型的目标是使控制变量的变化最小，其目标函数为：

39、

40、式中，且ws为ps的权重系数，反映控制的优先级；

41、所要满足的运行约束条件有：

42、

43、式中，psmin和psmax分别表示ps的最小值和最大值；n表示系统总线数；pg,i，pin,i分别为节点i的发电机或储能的出力；pl,i为节点i的负荷；vi，vj分别为节点i，j的电压，gij、bij为线路ij的电导和电纳；θij为节点i，j的电压相角差；iij为线路ij流经的电流，下标min、max分别表示对应参数的最小值和最大值。

44、本发明还提供了一种基于暂态电压稳定指标多项式逼近的暂态电压稳定预防控制系统，其特征在于，包括存储器、处理器以及存储于存储器上并能够被处理器运行的计算机程序指令，当处理器运行该计算机程序指令时，能够实现如上述所述的方法步骤。

45、本发明还提供了一种计算机可读存储介质，其上存储有能够被处理器运行的计算机程序指令，当处理器运行该计算机程序指令时，能够实现如上述所述的方法步骤。

46、相较于现有技术，本发明具有以下有益效果：本发明方法，首先，引入了一个将控制变量映射到某一特定tvsi(transient voltage stability index,tvsi)的隐式函数。其次，引入基于配点法的多项式逼近方法来逼近隐函数，相较于传统基于解析的预防控制方法，该近似多项式只包含控制变量。然后，基于近似多项式构造暂态电压稳定约束，将预防控制模型转化为一个非线性规划(non-linear programmingnlp)问题，该问题易于用内点法求解。通过实际系统的实例分析，验证了所提出的预防控制方法的可行性和准确性；通过本发明方法能够较快获得相应预防控制措施，从而达到维护电力系统安全稳定运行的目的。