基于特征模型和惯量估计的高精度伺服控制方法及系统与流程

本发明属于永磁同步电机驱动控制，特别是一种基于特征模型和惯量估计的高精度伺服控制方法及系统。

背景技术：

1、随着现代工业需求的日益增长，高精度伺服系统成为制造业发展的一个重要方向。普通伺服系统和一般控制器的性能已无法满足高需求的工业指标，亟需面向大惯量伺服系统的高精度伺服控制方法及系统。

2、伺服系统在高精度运行时工况复杂，系统参数容易产生变化，此外负载扰动也会影响系统的动态性能。传统的pid控制器参数固定，控制方法简便，在低阶线性系统的控制中具有良好效果。但在具有高阶、非线性、强耦合特点的伺服系统调速系统中，一般控制器对于负载扰动、参数变化等非线性扰动的影响没有较好的抑制效果，系统控制效果及精度难以满足性能指标的要求。因此，设计高精度伺服控制的新方法对满足高需求的工业指标、提高电机伺服控制性能具有很大的意义。

3、在目前的工程中，常采用传统pid控制器，在面对工况复杂、外部干扰大等情况时，难以满足高精度伺服控制的需求。对于使用一般的电机建模来完成伺服控制的方法来说，可能存在计算量大等问题。此外，通常的电机伺服控制不考虑负载惯量的变化，容易在负载发生较大变化时对伺服系统稳定性造成影响。

技术实现思路

1、本发明的目的在于提供一种基于特征模型和惯量估计的高精度伺服控制方法及系统，解决目前的高精度永磁同步电机伺服控制器面对系统参数变化和负载扰动时控制效果和精度不足的问题，以增强伺服控制的鲁棒性，实现永磁同步电机的高精度运行。

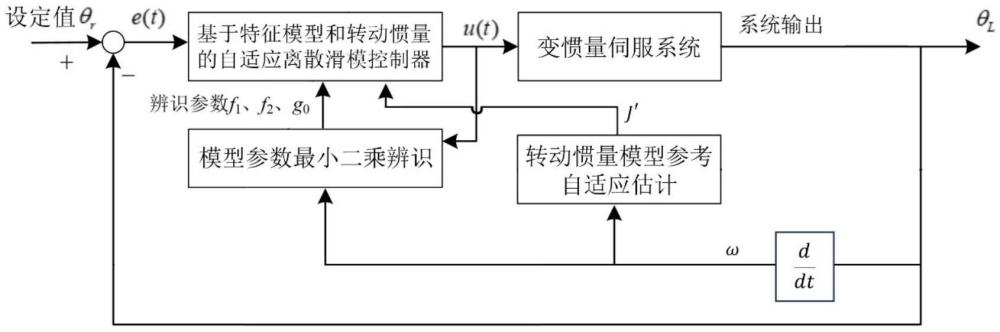
2、实现本发明目的的技术解决方案为：一方面，提供了一种基于特征模型和惯量估计的高精度伺服控制方法，所述方法基于伺服系统的特征模型与估计得到的负载惯量设计自适应控制器，以此实现高精度伺服控制。

3、进一步地，所述方法包括：

4、步骤1，基于伺服系统的动力学模型建立伺服系统的特征模型；

5、步骤2，利用模型参考自适应算法对转动惯量进行估计；

6、步骤3，基于步骤1中的特征模型与步骤2中的转动惯量，设计自适应离散滑模控制器完成对电机的高精度伺服控制。

7、进一步地，步骤1具体包括：

8、步骤1-1，建立伺服系统的动力学模型；

9、d轴电流id＝0，控制策略的永磁同步电机简化数学模型为：

10、

11、其中，lq是电机q轴等效电感，iq是q轴电流，uq是q轴电压，rs是定子q轴等效电阻，ce是q轴等效反电动势系数，ω是电机机械角速度，是电机机械角加速度，te是电磁转矩，ct是等效转矩系数，j是电机转子转动惯量，b是电机转子粘性摩擦系数，tl是电机侧负载转矩，t表示t时刻；

12、由所述简化数学模型得到永磁同步电机动力学方程：

13、

14、其中，θc是电机机械角位置，是θc关于t的一阶导数，tf是电机轴上摩擦力矩，tc是齿轮力矩，rc是减速器减速比，d1、d2是相对误差；

15、步骤1-2，建立伺服系统的特征模型；

16、对θc进行二阶差分，得到：

17、

18、其中，

19、

20、式中，是iq关于t的一阶导数，是θc关于t的二阶导数，d1、d2是相对误差；

21、对上式进行离散化，以t为采样周期，在kt时刻对θc(k+1)t和θc(k-1)t进行泰勒展开，并用θc(k)取代θc(kt)，整理得到：

22、

23、其中，θc(k-1)、θc(k)、θc(k+1)分别是k-1时刻、k时刻、k+1时刻对应的θc，δc是θc的迭代误差；

24、由此得到永磁同步电机的特征模型：

25、θc(k+1)＝f1(k)θc(k)+f2(k)θc(k-1)+g0(k)uq(k)

26、其中，

27、

28、进一步地，步骤1还包括：

29、步骤1-3，设计特征参数的在线辨识方法：在线辨识模型参数时采用带遗忘因子的最小二乘法进行计算：

30、

31、其中，k、p是最小二乘法的迭代矩阵，k(k)是k时刻对应的k，p(k)、p(k-1)分别是k时刻、k-1时刻对应的p；分别表示k时刻特征参数f1(k)，f2(k)，g0(k)的估计值，表示该估计值的转置，表示k-1时刻系统特征参数向量估计值的转置，φt(k)表示k时刻系统特征参数向量的转置，ψ(k)是系统数据向量，ψt(k)是ψ(k)的转置；em(k)是k时刻模型估计误差；λ1是遗忘因子。

32、进一步地，步骤2具体包括：

33、步骤2-1，由转矩方程建立永磁同步电机的参考模型；

34、转矩方程为：

35、

36、其中，te是电磁转矩，tl是负载的扰动转矩，jm是电机转动惯量，jl是负载转动惯量，ωm是转子机械角速度；

37、系统的采样时间为t，将所述转矩方程离散化，得到：

38、

39、其中，te(k-1)是k-1时刻对应的te，tl(k-1)是k-1时刻对应的tl，ωm(k)、ωm(k-1)分别是k时刻、k-1时刻对应的ωm，j是电机转动惯量jm和负载转动惯量jl之和，j＝jm+jl；

40、递推k-2时刻，有：

41、

42、认为负载转矩不变，有tl(k-1)＝tl(k-2)，整理上式，有参考模型：

43、

44、其中，ω(k)、ω(k-1)、ω(k-2)分别是k时刻、k-1时刻、k-2时刻对应的ω，δte(k-1)是k-1时刻te的变化量，j(k)是k时刻对应的j；

45、步骤2-2，建立转动惯量估计的可调模型：

46、

47、其中，ω′为离散化后的电机转子角速度，ω′(k)、ω′(k-1)、ω′(k-2)分别是k时刻、k-1时刻、k-2时刻对应的ω′，j′是可调模型估计得到的转动惯量，j′(k)是k时刻对应的j′；

48、步骤2-3，基于所述参考模型与可调模型的差值δω(k)＝ω(k)-ω′(k)，设计转动惯量估计的模型参考自适应算法，公式如下：

49、

50、其中，j′(k-1)是k-1时刻对应的j′，δ是可调参数；

51、步骤2-4，利用所述自适应算法对转动惯量进行估计。

52、进一步地，步骤3具体包括：

53、步骤3-1，定义控制误差面：

54、

55、其中，e为跟踪误差，e(k)、e(k-1)分别是k时刻、k-1时刻对应的e，s(k)是k时刻的控制误差面；

56、步骤3-2，设计滑模函数：

57、

58、其中，c为大于0的常量，e(i)是i时刻对应的e；

59、由滑模控制的原理，设计自适应离散滑模控制器如下：

60、

61、其中，λ为可调参数；

62、步骤3-3，根据步骤2中得到的转动惯量观测值分段设计不同的λ；

63、步骤3-4，利用经上述过程生成的自适应离散滑模控制器完成对电机的高精度伺服控制。

64、另一方面，提供了一种基于特征模型和惯量估计的高精度伺服控制系统，所述系统包括：

65、第一模块，用于基于伺服系统的动力学模型建立伺服系统的特征模型；

66、第二模块，用于利用模型参考自适应算法对转动惯量进行估计；

67、第三模块，用于基于第一模块的特征模型与第二模块的转动惯量，设计自适应离散滑模方法完成对电机的高精度伺服控制。

68、本发明与现有技术相比，其显著优点为：

69、(1)工程中的电机伺服系统常采用传统pid控制器，在面对工况复杂、外部干扰大等情况时，难以满足高精度伺服控制的需求。对于使用一般的电机建模来完成伺服控制的方法来说，可能存在建模工作量大、实时运行计算量大等问题。本方法在电机伺服控制中引入特征模型，将原系统的必要信息压缩到建立的特征模型的参数中，从而得到一个由低阶线性时变差分方程构成、可以用于描述复杂系统的特征模型。在系统运行时，通过实时辨识特征模型参数，可以解决复杂非线性对象难以建模的问题，大大方便了自适应控制器的设计。此外，特征建模可以克服原始动力学模型的不足之处，同时也能满足武器系统高精度运动控制的需求。

70、(2)传统伺服控制结构通常不考虑负载惯量的变化。在大惯量、高精度场合的伺服系统中，由于电机受到损耗、干扰及实际用途的影响，转动惯量无法保持恒定。为了获得更好的控制效果，可以对伺服系统的转动惯量进行在线估计，本发明根据负载惯量实时调整伺服系统的控制策略，能进一步提高基于特征模型设计的控制器的控制精度。

71、(3)本发明利用特征模型参数和估计转动惯量来设计自适应离散滑模方法，在考虑模型参数和转动惯量变化的基础上，设计自适应离散滑模控制器，来抑制位置传感器故障导致的位置信息波动对于跟踪控制精度的影响，能进一步提高系统的鲁棒性。

72、下面结合附图对本发明作进一步详细描述。