基于滚动时域估计的三电平发电系统多步预测控制方法

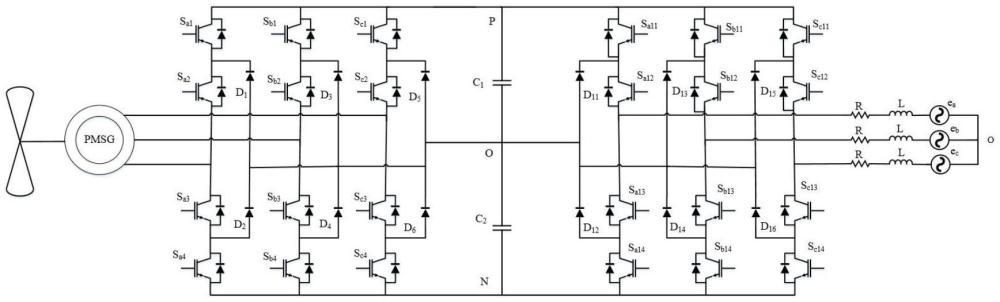
本发明涉及风力发电，具体涉及一种基于滚动时域估计的三电平发电系统多步预测控制方法。

背景技术：

1、随着工业化的迅速发展，环境污染、能源短缺问题也愈发突出。而电力作为一种高效、清洁、无污染、管理单一的能源形式，如何利用自然能高效发电成为了各国广泛关注的研究热点。

2、近年来，永磁直驱发电系统在风力发电领域受到了广泛关注。该系统具有低风速下发电效率高、直接驱动(无齿轮箱)等优点，然而传统pid控制方法需要对风力发电系统进行精确建模，而风力发电系统的复杂特性使得精确建模变得困难，导致其控制效果不佳。针对这些问题，国内外学者提出了多种先进控制策略。如预测电流控制、滑模变结构控制、自抗扰控制等。

3、相比于pid控制，有限集模型预测控制的控制器的设计更加的灵活，可以根据实际的控制目标构建出成本函数，另一方面有限集模型预测控制可以根据构建的成本函数输出直接作用于变换器的最优开关状态而无需调制环节，大大加快了系统的动态响应；自抗扰控制由于是采用二自由度的结构，能够很好地均衡跟踪性能和抗扰性能。利用dq轴差分观测器实时估计系统的外部扰动、不确定性因素，并在控制器端进行补偿，在满足跟踪控制性能的同时增强了系统的扰动抑制能力。

4、为改善永磁直驱风力发电系统的动态响应以及抗扰性能，在三电平的拓扑结构下，在外环采用预测控制进行预测估计；内环采用基于球形译码的多步预测控制，并设计相应的dq轴差分观测器进行补偿。传统的自抗扰控制只能较好的估计并补偿常值非匹配扰动，对于非匹配扰动的时变扰动时不能很好的估计并进行补偿，故设计dq轴差分观测器来抑制扰动，使得所设计的电流环控制器对参数不匹配有较强的抑制。另一方面传统的两电平拓扑结构只能通过提高开关频率来减少输出的谐波，但过高的开关频率会增大开关损耗，而多电平的拓扑可以使得开关器件在每个周期内开关一次达到的效果和传统换流器开关几次一致，故在相同的开关频率下，可以消除更多的谐波分量。因此为减少谐波分量，永磁直驱风力发电系统机侧网侧变流器采用二极管钳位型三电平拓扑结构，在一定程度上改善了开关损耗大、高谐波问题。

技术实现思路

1、为了克服现有技术的不足，本发明提供了一种基于滚动时域估计的三电平发电系统多步预测控制方法。在三电平的拓扑结构下，外环采用预测控制进行预测估计；内环采用基于球形译码的多步预测控制，并设计相应的dq轴差分观测器进行补偿，从而解决技术问题。

2、为了解决上述技术问题本发明提供的技术方案为：

3、基于滚动时域估计的三电平发电系统多步预测控制方法，包括以下步骤：

4、步骤1：通过风速捕捉，确定机侧速度环的给定转速值ωref；

5、步骤2：建立机侧数学模型；

6、步骤3：对机侧电流、速度采样和clark-park变换，过程如下：

7、首先实时采集机侧变换器三相电流ia,ib,ic，然后对采集到的ia,ib,ic进行clark变换得到α-β坐标系下的分量值iα,iβ，并在α-β坐标系下进行park变换，就可将α-β坐标系下的分量值iα,iβ转换为d-q坐标系下的分量值id,iq；

8、步骤4：建立离散的永磁同步发电机速度预测模型，过程如下：

9、永磁同步发电机的动态数学方程为：

10、

11、其中pn为表贴式永磁同步发电机极对数，ψf为表贴式永磁同步发电机磁链，tm为表贴式永磁同步发电机转矩，j为转动惯量，b为电机摩擦系数。

12、对进行拉普拉斯变换得出一阶模型，再进行欧拉离散，得到离散时间模型：

13、ωr(k)＝aiq(k-1)-bωr(k-1)

14、ωr(k+1)＝aiq(k)-bωr(k)

15、其中ωr(k)为kt时刻电机的实际转速，b＝-e-tb/j，对上式进行整理得速度预测模型如下：

16、

17、其中，ωm(k+1)为(k+1)t时刻的预测输出，为kt时刻表贴式永磁同步发电机的q轴电流控制增量。

18、当预测步长扩展到n步时，可以得到：

19、

20、其中，a＝-b，b＝a；δiq(k)为kt时刻表贴式永磁同步发电机的q轴电流控制增量，ai表示对矩阵a进行i次方后得到的矩阵。

21、可以简化为：

22、wωm(k)＝wωr(k)+gδiq(k)

23、其中，

24、

25、步骤5：建立离散的永磁同步发电机电流预测模型，过程如下：

26、根据坐标变换理论可以得到d-q坐标系下的表贴式pmsg数学模型其电压方程为：

27、

28、其中：ud,uq为27种开关状态对应下定子电压d,q轴电压分量；id,iq表示d-q坐标系下的定子电流d,q轴分量；ls为表贴式永磁同步发电机中d-q坐标系下定子电感；rs表示定子电阻；ψf表示永磁体磁链；ωre表示电角速度。

29、采用前向欧拉公式对电流状态方程进行离散化并经过一步延迟后得到离散永磁同步发电机电流预测模型如下形式：

30、

31、其中，id(k+1)，iq(k+1)为经过延时补偿后d-q坐标系下的定子电流d,q轴分量；id(k+2)，iq(k+2)分别为k+1时刻d,q轴定子电流预测值；ωre(k+1)近似等于ωre(k)；

32、考虑到系统参数的不确定以及外部扰动的影响，对上式经欧拉离散的电流方程进行整理变为矢量形式：

33、idq(k+1)＝aidq(k)+bpu(k)+c+bdd(k)

34、其中，其中，

35、idq＝[id iq]t，u(k)＝[sa sb sc],

36、d(k)＝[dd(k) dq(k)]t，

37、其中sa,sb,sc分别表示逆变器的三个桥臂上下三个开关的状态，udc表示直流母线电容两端电压。

38、当预测步长扩展到n步时，假设预测范围内电机的转子速度不变，并且定义：

39、

40、其中，i(k)代表在kt时刻对未来n个时间步长的dq轴电流预测值的矩阵，i*(k)代表在kt时刻对未来n个时间步长的dq轴参考电流矩阵，代表在kt时刻对未来n个时间步长的集总扰动估计值的矩阵。

41、从而，可以得到：

42、

43、其中

44、步骤6，构建成本函数；

45、构建出一个成本函数，来更好地表示出预测值对于期望值的跟踪效果，其成本函数j1形式如下：

46、

47、其中，表示定子电流d,q轴分量的参考值；idq(l+1)分别为l+1时刻d,q轴定子电流预测值，u为开关频率预测，λ表示权重系数。

48、为了符合球形译码算法的计算规律，将其整理变形为如下j1形式：

49、

50、其中，把带入成本函数j1，利用配方法将j1进一步进行整理，可以得到：

51、j1＝u(k)thu(k)+2θ(k)tu(k)+θ(k)＝(u(k)+h-1θ(k))th(u(k)+h-1θ(k))+const(k)其中，const(k)是与u(k)无关的常数，故该常数项与开关切换序列无关，此时可以将优化问题转化为：

52、

53、由于矩阵h为正定对称矩阵，可对式求解得到uunc(k)＝-h-1θ(k)，得到新的成本函数j'1：

54、j'1＝(u(k)-uunc(k))th(u(k)-uunc(k))

55、其中，uunc(k)为无约束条件下的最优解。

56、借助矩阵h为正定对称矩阵，可以得出它的逆矩阵也为正定矩阵；因此存在唯一的可逆下三角矩阵v，满足：

57、h-1＝vvt

58、令则将成本函数j'1进行变形得到如下式：

59、

60、其中，v-1是下三角矩阵。

61、构建出一个成本函数，来更好地表示出预测值对于期望值的跟踪效果，其成本函数j2形式如下：

62、

63、需要对未来优化时域中的误差进行预测，并且进行补偿可得

64、e(k)＝ωr(k)-ωm(k)且e(k)＝e(k+1)＝…＝e(k+n)

65、为了向设定集光滑过渡，取一阶指数变化的形式，参考轨迹方程如下：

66、yp(k+j|k)＝ωref(k+j)-αj[ωref(k)-ωr(k)],j＝1…n

67、其中，ωref(k)为设定值，α为权重系数，yp(k+1)为参考轨迹决定的期望输出。

68、经过预测矫正得

69、ω'r(k+j|k)＝yp(k+j|k)+e(k)，j＝1…n

70、其中，ω'r(k+j|k)为经过矫正后的参考速度，e(k)表示预测误差。

71、经简化将上述成本函数简化为：

72、

73、其中，

74、步骤7，选择最优电压矢量；

75、首先由三电平逆变器三个桥臂的的开关状态，确定其输出电压矢量；然后在预测模型的作用下，可以得到当前时刻下的预测值；最后根据设计的成本函数来选择最优电压矢量uopt_1：

76、uopt_1＝argmin j'1

77、首先采集当前时刻的参考转速；然后在预测模型的作用下，可以得到当前时刻下的转速预测值；最后根据设计的成本函数来选择最优电压矢量uopt_2：

78、uopt_2＝argmin j2

79、步骤8，dq轴差分观测器过程如下：

80、考虑到系统参数的不确定以及外部扰动的影响，步骤5中的永磁同步发电机方程可以整理为：

81、令x1(k)＝id(k)，则

82、

83、其中，dd(k)表示集总扰动，f1(k)、f2(k)、f3(k)分别表示dd(k)的一阶导数，二阶导数，三阶导数。

84、令设计相应得观测器，则

85、

86、选择合适的观测器增益β1,β2,β3,β4使得设计的dq轴差分观测器实现渐近收敛。此时需要从观测器的估计值中提取多步fcs-mpc每一步所涉及到扰动信息。具体的提取公式如下所示：

87、

88、同理，针对q轴设计类似的观测器。根据提取到的dq轴差分观测器的扰动信息，可以很容易得到球形译码预测模型中所需的

89、步骤9，引入状态变量dωl，确定新的状态空间模型；

90、在电机的实际调速过程中，转速外环的稳态性能会受到外部扰动和模型参数的不确定影响，机械运动方程为：

91、

92、由于模型参数的不确定和外部扰动的影响，引入变量dωl，将上述机械运动方程变成该形式：

93、

94、其中，表示机侧集总扰动；表示扰动补偿后的机侧控制器端控制量；ω表示机械角速度。

95、令x11＝ω，x12＝dωl为新的状态变量，则新的状态空间模型表示为：

96、

97、其中，x11＝ω表示机械角速度，x12＝dωl表示集总扰动，x13为x12的一阶导数，h1表示dωl的二阶微分,表示扰动补偿后的机侧控制器端控制量。

98、步骤10，差分gpio观测器设计，过程如下：

99、根据步骤9中的新状态空间模型设计差分gpio观测器其形式为：

100、

101、其中，表示误差变量，表示ω的估计值，表示集总扰动的估计值，为集总扰动一阶导数的估计值；表示扰动补偿后的机侧控制器端控制量；

102、β11,β12,β13,β14表示扩张状态观测器的增益；

103、令采用前向欧拉公式对上式进行离散化得到：

104、

105、此时需要从差分gpio观测器的估计值中提取β11,β12,β13,β14多步速度预测每一步所涉及到扰动信息。具体的提取公式如下所示：

106、

107、步骤11，建立直流环节数学模型；

108、步骤12，建立网侧数学模型；

109、步骤13，对网侧电流、电压采样和坐标变换；

110、步骤14，建立离散内环功率预测模型；

111、步骤15，构建成本函数；

112、步骤16，选择最优电压矢量；

113、步骤17，引入状态变量dul，确定新的状态空间模型；

114、步骤18，设计扩张状态观测器；

115、步骤19，网侧外环控制律设计。

116、进一步的，所述步骤11中，直流侧电容节点p、o、n处电流表示为：

117、

118、ic1＝ipm-ipg

119、ic1+iom＝ic2+iog

120、ic2+inm＝ing

121、其中，c1,c2表示直流滤波电容；uc1,uc2表示直流母线电容上的电压；ic1,ic2表示流过直流滤波电容的电流；ipm,iom,inm表示机侧流经节点p、o、n处电流，ipg,iog,ing表示流向网侧节点p、o、n处电流。

122、进一步的，所述步骤12中，在d-q坐标系下的网侧数学模型为：

123、

124、其中，ud,uq为三电平逆变器输出电压在d-q坐标系下的分量；ed,eq为网侧电压在d-q坐标系下分量；id,iq为网侧电流在d-q坐标系下分量；l表示网侧滤波电感；r表示输出端等效电阻；ωge表示电网角速度。

125、进一步的，所述步骤14中，网侧逆变器采用电压定向控制的方法，故基于电网电压矢量定向的网侧逆变器电流方程可以表示为：

126、

127、其中，ed为网侧电压d轴分量。

128、进一步的，所述步骤15中，构建出一个成本函数，成本函数j3形式如下：

129、

130、其中，p*,q*表示有功功率与无功功率参考值；p(k+1),q(k+1)分别为(k+1)ts时刻有功功率与无功功率的预测值。

131、进一步的，所述步骤16中，从网侧逆变器输出的27个电压矢量中选择出使得成本函数j2最小的电压矢量uopt_3：

132、uopt_3＝argmin j3

133、进一步的，所述步骤17中，引入状态变量dul，构建新的状态空间模型；

134、在不考虑变换器损耗的情况下，机侧整流器的输出功率pm可以表示为：

135、pm＝udcim

136、其中，udc表示直流母线电压，可以表示为udc＝uc1+uc2；im表示由机侧变换器输出到直流母线的电流；

137、流过直流侧电容的电流为：

138、

139、其中，c表示直流侧电容，可以表示为c＝c1＝c2；ig表示输入到网侧逆变器的电流；

140、从直流侧输入到网侧逆变器的有功功率p为：

141、p＝udcig

142、由上述等式可以得到：

143、

144、等价于

145、

146、其中，表示网侧电压环集总扰动；bu0是关于bu的估计值，其中p*表示有功功率参考值；

147、令z1＝udc；z2＝dul，则新的状态空间模型为：

148、

149、其中，h2表示dul的微分；bu0是关于bu的估计值，其中p*表示有功功率参考值。

150、进一步的，所述步骤18中，外环的改进扩张状态观测器表示形式如下所示：

151、

152、其中，表示udc的估计值；表示集总扰动dul的估计值；l1,l2,l3表示改进后的扩张状态观测器的增益；

153、进一步的，所述步骤19中，外环环控制律设计如下所示：

154、选择合适的观测器增益l1,l2,l3，可以由步骤18中设计的扩张状态观测器得到直流母线电压的估计值以及外环集总扰动的估计值由扩张状态状态观测器得到估计值可以用于控制器的设计，具体形式如下所示：

155、

156、其中，表示电压外环的参考值；uu0表示网侧控制器输出；kup表示控制器增益。

157、本发明设计构思：

158、本发明基于机侧、网侧变换器采用三电平结构，在新的拓扑下建立数学模型；模型离散化处理；对电流、电压、速度进行采样以及坐标变换；设计外环模型预测速度控制器；设计内环模型预测电流控制器；根据所构建的成本函数选择出使得成本函数值最小的最优电压矢量；借助dq轴观测器来对系统dq轴扰动的信息进行估计，使得所设计的电流环控制器对参数不匹配有较强的抑制；借助差分gpio观测器分别对系统的状态信息以及多步预测每一步所涉及到扰动信息进行估计，构建出新的状态空间模型；本发明提供了一种基于滚动优化的三电平发电系统球形译码多步预测控制方法，对传统的有限集模型预测控制策略进行了优化，对外环采用预测控制进行预测估计，大大的降低了计算量大的问题并有效地增强了系统的抗扰性能。

159、本发明的有益效果为：

160、本发明对于三电平发电系统的外环均采用预测控制进行预测估计；电流环采用多步球形译码模型电流预测控制来代替传统的pi控制器，其无需调制器的优点，使得三电平发电系统的动态响应速度提高，并相比于传统的fcs-mpc大大降低了计算量。同时还设计了dq轴差分观测器使得所设计的电流环控制器对参数不匹配有较强的抑制。