一种基于Lyapunov的LC滤波四桥臂逆变器自适应控制方法

本发明涉及电力电子，尤其涉及一种基于lyapunov的lc滤波四桥臂逆变器自适应控制方法。

背景技术：

1、四桥臂逆变器已被应用于微电网、新能源发电并网、三相永磁同步电机驱动、不间断电源和电动汽车充电桩等场合，因具有功率密度大、直流母线电压利用率高和带负载能力强等特点，而被广泛研究。四桥臂逆变器将直流电变换为交流电的控制过程大多可描述为：首先利用输出端参考信号和测量信号，经控制律得到逆变器参考信号；然后利用载波调制或空间矢量调制等方法，生成脉冲信号，对逆变器开关器件进行控制；最后利用滤波器滤除高频谐波后，在输出端得到期望输出。

2、常见的逆变器控制方法分为线性控制和非线性控制。线性控制以比例积分控制和比例谐振控制为代表。比例积分控制的常见做法是将三相交流信号从静止坐标系变换至旋转坐标系，以实现零稳态误差控制，其结构简单，但参数整定较为困难，且动态调节时间较长。基于内模原理的比例谐振控制，无需坐标变换即可对正弦信号进行零稳态误差跟踪，缺点是需设计多个谐振环节来达到放大基波信号和抑制谐波信号的目的，导致控制系统较为复杂。

3、在应对逆变器系统的离散非线性特性时，非线性控制体现出了巨大优势。其中，模型预测控制是近年来的研究热门，这种控制方法将系统动态方程离散化，由当前和过去时刻的状态预测下一时刻的输出，根据代价函数最小原则，选取最优控制矢量。这种方法具有良好的动态和稳态性能，但开关频率不固定，系统计算负担较重。无差拍控制通过对系统的精确建模，利用采集的状态量和下一时刻参考输出量，计算出下一个开关周期的脉冲宽度，这种方法实现简单，稳态和动态效果良好，缺点是参数鲁棒性较差。滑模控制以状态变量的误差和误差导数构建滑动面，根据当前状态与滑动面的相对位置来控制逆变器，这种方法常与重复控制相结合，在有限时间内限制滑动面，具有良好的动态性能，然而其固有的抖振问题需要注意。

4、上述控制方法各有优缺点，但存在一个共同的局限性，即不能严格保证闭环控制系统全局渐进稳定。针对该问题，有学者提出了基于lyapunov的单环控制方法，保证了系统稳定性，并成功应用于dc-dc变换器、三相ac-dc整流器、单相有源滤波器、单相并网光伏逆变器和单相lcl滤波并网逆变器等电力电子系统控制。经典的基于lyapunov的控制方法将lyapunov函数表示为电容电压和电感电流的跟踪误差线性平方和，求解占空比以保证能量函数导数的负定性，进而得到控制律，这种控制方法属于单环控制，存在稳态误差。h.komurcugil团队提出了一种扩展的基于lyapunov的单相ups逆变器控制方法，首次在基于lyapunov的控制方法中引入了电压环，提出的电压电流双环控制方法消除了稳态误差。sefa团队将基于lyapunov的双环控制方法应用于单相和三相lcl并网逆变器。r.gavagsaz-ghoachani团队首次利用lyapunov稳定理论同时完成了电流观测器和控制律的设计，构建了基于lyapunov的单相lc滤波整流器自适应控制律，在获得系统全局稳定性的同时，节省了电流传感器。何劲松等结合了h.komurcugil团队和r.gavagsaz-ghoachani团队控制方法的优点，提出了基于lyapunov的单相和三相三桥臂逆变器自适应控制方法，在节省负载电流传感器的同时，保证了系统的全局渐进稳定性，并实现了零稳态误差控制。

5、基于lyapunov的自适应控制是一种极具吸引力的控制方法，该方法在四桥臂逆变器控制中的设计无法类比三桥臂逆变器，因为在三桥臂逆变器控制中，只需要观测一个负载导纳，系统状态方程从abc静止坐标系转换到dq0旋转坐标系使系统解耦后，控制目标由正弦交流量变为常量，待观测负载导纳矩阵可与状态向量分离，这使得构建自适应控制律和参数设计等工作变得十分简便，而四桥臂逆变器需处理不平衡负载情况，需观测多个负载导纳，在进行坐标变换时，待观测负载导纳矩阵与状态向量无法分离，所以基于lyapunov的四桥臂逆变器自适应控制律无法用类似方法来设计实现；当系统运行在小功率情况时，传统的基于lyapunov的逆变器自适应控制方法存在系统能量收敛速度慢的问题。

技术实现思路

1、针对上述现有技术的不足，本发明提出了一种基于lyapunov的lc滤波四桥臂逆变器自适应控制方法。首先利用反推法得到f桥臂端电压控制律与三相桥臂端电压控制律的关系，实现三相桥臂的解耦控制；然后将通过静态计算得到的电感电流初始参考值加上负载电压的线性误差项，得到优化的电感电流参考值，并结合lyapunov稳定理论设计三相桥臂端电压控制律和负载导纳观测器，所提方法无需负载电流传感器，保证系统在各种负载情况下具有全局渐进稳定性以及零稳态误差的输出电压，同时解决了当系统运行在小功率情况时，传统的基于lyapunov的自适应控制方法存在的系统能量收敛速度慢的问题。

2、本发明的技术方案为：

3、一种基于lyapunov的lc滤波四桥臂逆变器自适应控制方法，具体包括如下步骤：

4、步骤1：基于基尔霍夫电压定律，建立两电平四桥臂逆变器的电压动态方程组；

5、所述两电平四桥臂逆变器电压动态方程组的表达式为：

6、

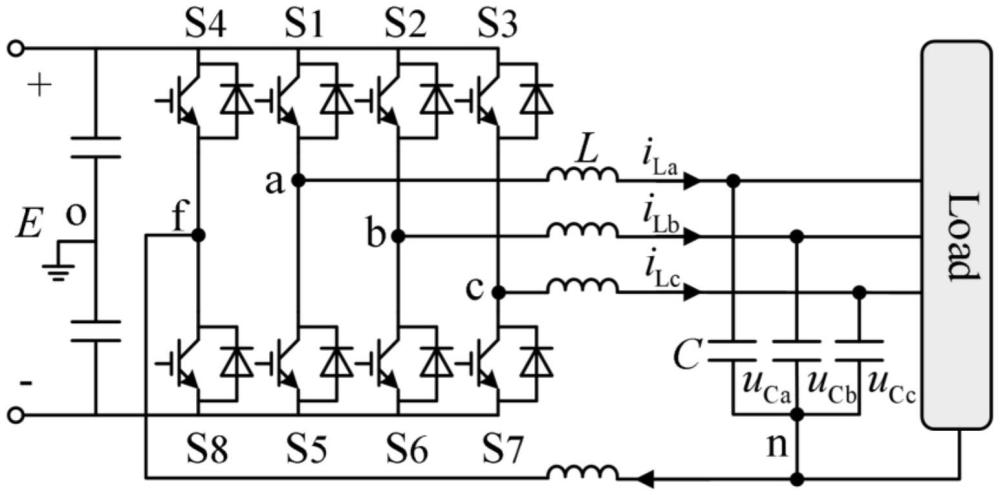
7、其中，uao、ubo、uco和ufo分别表示a相、b相、c相桥臂端电压和f桥臂端电压；uno表示负载中性点相对于直流侧电容中点的电压；ila、ilb、ilc和ilf分别表示a相、b相和c相电感电流和中性电感电流；uca、ucb和ucc分别表示输出侧a相、b相和c相电容电压(也表示负载电压)；l表示滤波电感；

8、步骤2：令负载中性点相对于直流侧电容中点的电压为零，消除步骤1得到的电压动态方程的公共项，并得到解耦后的两电平四桥臂逆变器的电压动态方程组；

9、令uno＝0，并将其代入到步骤1的电压动态方程组中，消除电压动态方程的公共项，使得代表三相桥臂的三个电压动态方程解耦，并得到解耦后的两电平四桥臂逆变器的电压动态方程组；

10、所述的解耦后的两电平四桥臂逆变器的电压动态方程组的表达式为：

11、

12、步骤3：将步骤2得到的解耦后的电压动态方程组中的四个电压动态方程相加，得到总体电压动态方程；基于基尔霍夫电流定律，建立两电平四桥臂逆变器的电流动态方程组；将四个桥臂的电感电流关系式代入到总体电压动态方程中，消除电感电流项，得到f桥臂端电压控制律与三相桥臂端电压控制律的关系式；

13、步骤3.1：将步骤2的方程组(2)中的四个桥臂的电压动态方程相加，得到总体电压动态方程；

14、所述的总体电压动态方程的表达式为：

15、uao+ubo+uco+ufo＝ldila/dt+ldilb/dt+ldilc/dt-ldilf/dt+uca+ucb+ucc (3)

16、步骤3.2：基于基尔霍夫电流定律，建立两电平四桥臂逆变器的电流动态方程组；

17、所述的两电平四桥臂逆变器电流动态方程组的表达式为：

18、

19、其中，ga、gb和gc分别表示a相、b相和c相负载导纳的实际值；c表示滤波电容；

20、步骤3.3：将方程组(4)中的四个桥臂的电感电流关系式代入到总体电压动态方程中，消除电感电流项，得到f桥臂端电压控制律与三相桥臂端电压控制律的关系式，具体表达式为：

21、ufo＝uca+ucb+ucc-uao-ubo-uco (5)

22、步骤4：以a桥臂为例，定义负载电压参考值和负载导纳估计量；定义负载电压的跟踪误差和虚拟负载导纳的估计误差；将负载电压参考值代入到步骤2得到的解耦后的动态方程组中，在系统处于稳态的假设条件下得到电感电流初始参考值；将电感电流初始参考值加上负载电压的线性误差项，得到优化的电感电流参考值；定义电感电流的跟踪误差；

23、步骤4.1：定义负载电压参考值为ucaref，其中，ucaref为已知时变正弦交流量，幅值为um，角频率为ω；定义负载导纳的估计量为

24、步骤4.2：定义e2,e3分别为负载电压跟踪误差和虚拟负载导纳估计误差，具体表达式为：

25、

26、步骤4.3：假设系统处于稳态，将uca＝ucaref代入到电流动态方程中，得到电感电流初始参考值ilaref；

27、所述的电感电流初始参考值的表达式为：

28、

29、步骤4.4：将电感电流初始参考值加上负载电压的线性误差项，得到优化的电感电流参考值ilaref1；

30、所述的优化的电感电流参考值的表达式为：

31、

32、其中常数τ(τ＞0)为控制参数，用以调整优化的电感电流参考值与负载电压误差的关系；

33、步骤4.5：定义e1为电感电流跟踪误差，具体表达式为：

34、e1＝ila-ilaref1 (9)

35、步骤5：用步骤4定义的三个误差构建李雅普诺夫函数；

36、用步骤4定义的e1,e2,e3构建李雅普诺夫函数，用于表征系统能量；

37、所构建的李雅普诺夫函数的表达式为：

38、

39、其中，ρ,η(ρ＞0,η＞0)表示两个控制参数，用于分配各项能量的占比；

40、步骤6：对步骤5得到的李雅普诺夫函数和步骤4定义的三个误差求导，并将三个误差的导数代入到李雅普诺夫函数的导数中；以保证李雅普诺夫函数的导数在非稳定点处始终小于零为原则，构建含有未知参数的a桥臂负载导纳观测器和端电压控制律，同理得到b和c桥臂负载导纳观测器和端电压控制律，并根据步骤3.3得到含有未知参数的f桥臂端电压控制律；

41、步骤6.1：对步骤5中的李雅普诺夫函数求导数，具体表达式为：

42、

43、对负载电压、电感电流的跟踪误差和负载导纳的估计误差求导数，具体表达式为：

44、

45、将式(12)代入式(11)，得到李雅普诺夫能量函数导数的展开式，具体表达式为：

46、

47、将式(13)化简并整理，得到李雅普诺夫能量函数导数的分块展开式，具体表达式为：

48、

49、其中常数k(k＞τl/c)为控制参数，引入该参数是为了在电压控制律中加入电流误差项，从而加快系统动态响应速度；

50、步骤6.2：令α＝β＝0，推导出含有未知参数的a桥臂负载导纳观测器和端电压控制律；

51、所得到的a桥臂负载导纳观测器的表达式为：

52、

53、所得到的a桥臂端电压控制律的表达式为：

54、

55、b和c桥臂的负载导纳观测器以及端电压控制律的设计过程与a桥臂相似，进一步，根据步骤3.3，可得到含有未知参数的f桥臂端电压控制律；

56、步骤7：在保证系统满足快速动态响应和合适阻尼的要求下以及逆变器桥臂输出电压在线性范围内的约束条件下，得到参数取值区间；在上述参数取值区间内选择任意一组参数，代入到步骤6得到的观测器和控制律中，得到四个桥臂的端电压控制律，通过载波调制产生用于控制功率开关管通断的脉冲信号；

57、步骤7.1：对系统进行稳定性分析，可知参数在较大范围内(ρ,τ,η＞0，且k＞τlc)取值，不会影响系统全局大信号稳定性，而各桥臂端电压输出应在线性范围内，即应保证系统在动态过程中，各桥臂端电压控制律始终在-0.5e和0.5e之间，以上述原则确定本发明中合适的控制参数取值范围为ρ∈(2～11)，k∈(15～40)，τ∈(0.001～0.03)，η∈(160～500)；

58、步骤7.2：任选上述参数取值区间中的一组数据作为本发明的控制参数，所选控制参数具体为ρ＝7，k＝25.5，τ＝0.15，η＝300，并将控制参数代入到步骤6中得到的观测器和控制律中，得到四个桥臂的端电压控制律，通过载波调制产生用于控制功率开关管通断的脉冲信号。

59、采用上述技术方案所产生的有益效果在于：

60、本发明方法对传统的基于lyapunov的逆变器自适应控制方法进行了改进，实现了基于lyapunov的四桥臂逆变器自适应控制方法，并建立了改进的负载导纳观测器，节省了三个负载电流传感器。本发明方法不但保证系统具有全局渐进稳定性和零稳态误差的输出电压，而且与传统的基于lyapunov的逆变器自适应控制方法相比，保证了系统能量收敛速度始终与负载电压误差相关，提高了系统运行在小功率情况时的动态响应速度。