基于分布区间优化的电力系统无功优化方法及计算机介质

本发明涉及电力系统优化领域，尤其涉及一种基于分布区间优化的电力系统无功优化方法及计算机介质。

背景技术：

1、电力系统无功优化在确保电网安全、提高电压质量和减少电能损耗等方面具有至关重要的作用。近年来，风电、光伏等可再生能源的大规模并网，可再生能源的波动性和间歇性为电力系统带来了很强的不确定性，同时电力交易的频繁进行和电力负荷的多样化进一步增强了电力系统的不确定性。电力系统不确定性的增强导致电力系统的无功优化问题变得更加复杂且不确定。

2、传统的无功优化方法大多基于确定性优化模型，假设系统参数已知且确定，难以适用于当前背景下的电力系统，因此，越来越多学者将不确定性优化方法引入到电力系统无功优化中，形成了随机规划法、鲁棒优化法和区间优化法三类主要不确定性无功优化方法。随机规划法中，将不确定性参数视为遵循特定分布的随机变量，从而将无功优化模型转化为期望模型或机会约束规划模型，通过这种方式，能够获得在一定置信水平下，满足约束条件和优化目标的无功电压控制方案。然而，随机规划法需要不确定数据的概率分布信息，需要通过历史数据统计或经验模型生成大量场景，建模过程较粗糙且计算效率较低，同时不能保证不确定环境下电网电压的安全。鲁棒优化法不要求假设不确定性数据的概率分布，而是基于给定的不确定集，寻求在所有场景下都能满足约束条件的优化方案，虽然鲁棒优化提供的方案通常较为保守，能够应对不确定集内的各种不确定性，解决了随机规划方法在建模和计算时间上的复杂性，提升了方案的实际可行性，但在经济性方面则相对较弱；此外，由于无功优化属于非凸问题，鲁棒优化法只能用于凸优化，需要进行近似处理，可能引入一定的近似误差。

3、区间优化法中，将不确定性数据表示为区间建立优化模型，在区间优化模型中，状态变量表示为区间，控制变量为实数，寻求使状态变量满足约束条件且目标函数最优的控制变量。区间优化法建模简单，无需近似凸化处理，且获得策略在理论上能保证系统的安全。现有的区间优化法包括：智能算法求解方法，如采用遗传算法和粒子群算法等寻优以获得最优控制变量；近似优化方法，如通过区间泰勒展开区间无功优化，构造线性或二次规划的区间无功优化模型，降低求解难度；其他转化方法，如采用安全限定义法将区间模型转化为确定性模型进行求解。现有的区间优化法在处理模型中的状态变量时，均通过区间潮流算法求解区间潮流方程获得状态变量区间，可见区间潮流方程的求解在无功优化模型的处理中占有至关重要的地位。然而，现有的区间潮流算法获得的区间潮流解均偏保守，由于考虑了发生概率极低的极端场景，导致偏离真实范围，工程意义不大；同时这种情况下得到的区间无功优化策略经济性也较差。

4、因此，亟需一种新的技术方案，用以解决如何提升高新能源渗透率电力系统无功优化方法的精度、实用性和经济性的技术问题。

技术实现思路

1、本发明提供了一种基于分布区间优化的电力系统无功优化方法及计算机介质，用以解决如何提升高新能源渗透率电力系统无功优化方法的精度、实用性和经济性的技术问题。

2、为实现上述目的，本发明提供了一种基于分布区间优化的电力系统无功优化方法，包括以下步骤：

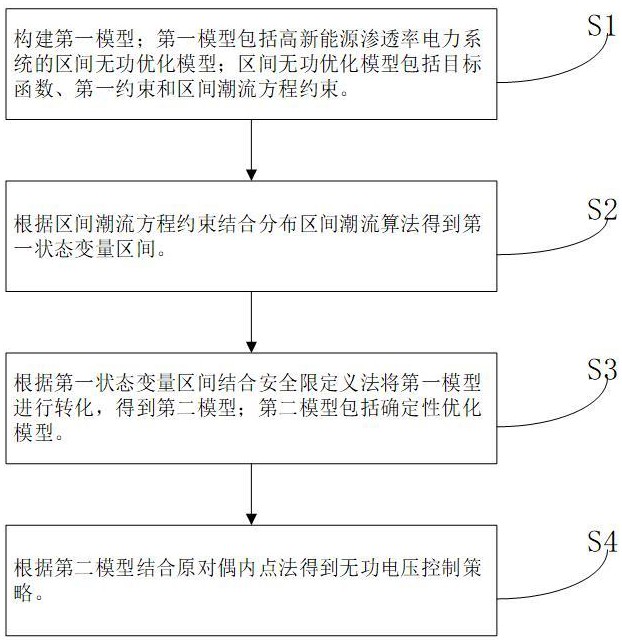
3、s1、构建第一模型；第一模型包括高新能源渗透率电力系统的区间无功优化模型；区间无功优化模型包括目标函数、第一约束和区间潮流方程约束。

4、s2、根据区间潮流方程约束结合分布区间潮流算法得到第一状态变量区间。

5、s3、根据第一状态变量区间结合安全限定义法将第一模型进行转化，得到第二模型；第二模型包括确定性优化模型。

6、s4、根据第二模型结合原对偶内点法得到无功电压控制策略。

7、优选的，目标函数包括：

8、以系统网络损耗为目标函数，包括：

9、；

10、其中，表示系统所有节点集合；和分别表示节点和节点；和分别表示节点和节点的电压幅值；为系统节点导纳矩阵的实部；，和分别表示节点和节点的电压相角。

11、优选的，区间潮流方程约束包括：

12、；

13、其中，表示系统节点导纳矩阵的虚部；表示可再生能源机组有功出力区间；和分别表示可再生能源机组有功出力区间的下边界和上边界；表示不包含平衡节点的发电机节点；表示平衡节点，一般系统中包括一个平衡节点；时，表示不包含平衡节点的发电机节点有功负荷；时，表示平衡节点的有功负荷；表示平衡机组有功出力；时，和分别表示不包含平衡节点的发电机节点无功出力和无功负荷；时，和分别表示平衡节点的无功出力和无功负荷；平衡节点和发电机节点的有功负荷和无功负荷为确定性数据；和分别表示负荷节点的有功负荷区间和无功负荷区间；和分别表示负荷节点有功负荷区间的下边界和上边界；和分别表示负荷节点无功负荷区间的下边界和上边界；表示负荷节点；表示节点的无功补偿容量。

14、优选的，第一约束包括：

15、；

16、其中，和分别表示节点电压幅值的下限和上限；和分别表示平衡机组有功出力的下限和上限；时，和分别表示不包含平衡节点的发电机节点无功出力的下限和上限；时，和分别表示平衡节点的无功出力的下限和上限；表示变压器变比；和分别表示变压器变比的下限和上限；表示变压器支路；和分别表示无功补偿容量的下限和上限；表示无功补偿节点。

17、优选的，s2包括：

18、通过分布区间潮流算法对区间潮流方程约束进行处理：

19、假设系统中节点总数为，除平衡节点外的发电机节点总数为；将区间潮流方程约束中的状态变量和表示为仿射形式；状态变量和的第一仿射表达式包括：

20、；

21、；

22、；

23、其中，和分别表示和的区间中点，可在系统注入功率区间中点处求解潮流方程取得；和为仿射噪声元，取值范围均为；和为灵敏度系数。

24、根据第一仿射表达式建立第三模型，第三模型包括区间潮流方程约束的场景优化模型，包括：

25、；

26、采用内点法求解第三模型，得到仿射噪声元最大值和最小值，进而得到高精度的状态变量仿射表达式，即得到状态变量和的第二仿射表达式：

27、；

28、；

29、；

30、对于区间的仿射表达式，噪声元变量和在区间内服从均匀分布，则第二仿射表达式可视为一系列均匀分布的叠加，且各式中每一项之间相互独立，即满足中心极限定理，和的取值近似服从正态分布；根据均匀分布的性质，得到第二仿射表达式中每一项的方差，包括：

31、；

32、；

33、；

34、其中，表示从或中任选其一。

35、根据方差得到状态变量和的标准差：

36、；

37、；

38、；

39、由于和的取值近似服从正态分布，根据正态分布性质得到状态变量置信度0.9973的置信区间：

40、；

41、；

42、；

43、即得到第一状态变量区间。

44、优选的，还包括：

45、求解灵敏度系数，包括：

46、；

47、其中，和表示各变量在0值处的偏导数，可在注入功率区间中点处的潮流解处取得；和分别表示有功和无功注入功率区间半径，，和分别表示发电机节点有功出力区间的上限和下限；，和分别表示负荷节点有功负荷需求区间的上限和下限；，和分别表示负荷节点无功负荷需求的上限和下限。

48、优选的，s3包括：

49、由于第一模型中的不等式约束均为单变量约束，将第一模型中的变量、目标函数和约束条件采用向量和函数表示，可将第一模型表示为紧凑模型：

50、；

51、其中，表示系统网络损耗；表示网络损耗的区间形式；表示区间潮流方程约束；表示节点注入功率区间向量；表示第一状态变量区间；表示控制变量；表示负荷节点电压和发电机无功出力构成的向量，和分别表示的最小值和最大值，和分别表示控制变量向量的最小值和最大值；表示求转置；将除平衡节点外节点的电压相角和平衡节点的有功出力表示为向量，则系统状态变量向量可以表示为。

52、在紧凑模型中，对于任意的控制变量，通过分布区间潮流算法求解区间潮流方程，得到对应的；由于有界，则存在控制变量向量使得中的一个的区间半径最大，记为，且每一个均存在一个对应；因此，定义的最大半径：

53、；

54、其中，表示状态变量的区间半径。

55、通过蒙特卡洛模拟，得到中所有变量区间半径最大值组成的向量；对于相同的控制变量，为区间潮流方程的解，为确定性潮流方程的解，考虑到确定性状态变量可能处于蒙特卡洛模拟中最大状态变量区间内的任意位置，同时确定性状态变量对应的状态变量区间最大半径为，则存在约束条件，保证满足紧凑模型中的约束条件；因此，定义绝对安全限，包括：

56、；

57、；

58、绝对安全限表示最坏场景下的安全边界，具有较强的保守性，引入平均位置比例对安全限进行修正，以降低安全限的保守性：

59、；

60、其中，表示控制变量在，场景在处的确定状态变量；和分别表示在处求解区间潮流方程得到的状态变量区间下边界和上边界；假设对应的平均位置比例为，，则修正安全限可通过如下关系式进行表示：

61、；

62、；

63、平均位置比例在控制变量中点处定义获得，而一般情况下控制变量为其区间内的任意取值，导致偏离，因此修正安全限存在安全误差，状态变量可能越限；取状态变量越上限幅度为，越下限幅度为，对状态变量进行精确修正，包括：

64、；

65、；

66、若精确修正后状态变量仍处于越限状态，则重复进行精确修正，直至状态变量不越限，得到最终安全限；根据最终安全限将紧凑模型转化为第二模型，第二模型可通过如下关系式进行表示：

67、；

68、其中，表示内的任意场景。

69、优选的，s4包括：

70、通过原对偶内点法求解第二模型：

71、对于第二模型，首先引入拉格朗日乘子以及对偶变量和构造拉格朗日函数，可通过如下关系式进行表示：；

72、建立拉格朗日函数的kkt条件，kkt条件包括梯度条件、原始可行性条件、对偶可行性条件和互补松弛条件，可通过如下关系式进行表示：

73、；

74、通过牛顿梯度下降求解kkt条件，包括：

75、选择初始点，确保满足不等式约束；在第次迭代中，基于当前的得到牛顿梯度下降方程，可通过如下关系式进行表示：

76、；

77、其中，为拉格朗日函数的海瑟矩阵，为牛顿步，包括和；表示当前的梯度；设为步长，得到牛顿步变量更新方案，可通过如下关系式进行表示：

78、；

79、其中，表示第次迭代的变量组成的向量，包含；表示第次迭代的变量向量，包含。

80、判断是否满足收敛条件，若满足，则判定牛顿梯度下降收敛，停止迭代，输出第二模型的求解结果，即得到无功电压控制策略；收敛条件包括对偶间隙小于收敛容差，且原始可行性条件、对偶可行性条件和互补松弛条件均满足。

81、优选的，还包括：

82、根据无功电压控制策略计算分布区间潮流，得到控制变量值和对应的第二状态变量区间，包括：

83、无功电压控制策略即求解结果中的控制变量包括最终变压器变比、发电机机端电压和无功补偿容量；根据控制变量得到下的分布区间潮流模型，可通过如下关系式进行表示：

84、；

85、其中，和为分别表示最终变压器变比下节点导纳矩阵的实部和虚部。

86、根据下的分布区间潮流模型结合分布区间潮流算法，求解得到对应的系统第二状态变量区间，包括负荷节点电压区间、节点电压相角区间和发电机无功出力区间；输出和，即得到控制变量值和对应的第二状态变量区间。

87、本发明还提供了一种计算机介质，包括处理器、存储器和实现本发明方法的计算机程序。

88、本发明具有以下有益效果：

89、本发明的基于分布区间优化的电力系统无功优化方法，通过分布区间潮流算法处理区间潮流方程约束得到的状态变量区间具有高置信度，使得本方法能够降低区间算法的保守性，更接近实际情况的范围，从而提高求解精度，同时降低系统网损，改善电压控制策略的经济性和实用性；通过安全限定义法将区间无功优化模型转化为确定性优化模型，并通过原对偶内点法求解确定性优化模型，使得本发明的方法解决了非线性区间优化算法的收敛性问题，能够得到更安全经济的区间电压控制策略。

90、除了上面所描述的目的、特征和优点之外，本发明还有其它的目的、特征和优点。下面将参照附图，对本发明作进一步详细的说明。