用于对数进行有理压缩和解压缩的方法和装置与流程

本领域一般涉及对诸如地震数据的数据进行的无损数据压缩。

背景技术：

数据压缩技术通常用于实现在信号的数字表示中的降低的比特率，以用于高效处理、传输和存储。在文件的总存储大小能够被减小时文件的内容被称为被动压缩。然而，取决于内容，存在对该减小的限制，其对压缩施加限制。压缩算法一般搜索内容的不同表示，以便减少存储内容所需要的空间。对于无损压缩的情况，结果是具有被恢复到确切原始未压缩文件的潜力的压缩文件，或者对于有损压缩的情况，结果是原始未压缩文件的近似或相似版本。用于恢复原始文件的算法被称为解压缩算法并且通常包括压缩算法的反向步骤。

例如，地震数据集的大小由于从更复杂的地质情况提取石油的需求而继续增大。因此，在地球物理应用中，地震数据压缩已经变得重要，以用于对地震数据的高效处理、存储和传输。因此，存在对用于压缩诸如地震数据的原数据和经处理的数据两者的改进的技术的需求。存在对使用关于数据的先验知识的无损压缩算法(例如，专用于数字的压缩算法)的进一步的需求。

技术实现要素：

本发明的说明性实施例提供了用于对数进行有理压缩的方法和装置，所述数诸如地震数据。在一个示范性实施例中，通过获得多个数(例如，整数和/或浮点数)来对一个或多个数进行压缩，其中所述多个数中的每个数使用零个或更多个位来表示以指示具有所述 给定数的给定底数的指数，并且具有表示具有所述给定数的有效位的数量的长度；针对所述多个数中的每个数，计算所述长度和所述长度与所述指数之间的差，并且在出现所述差时对所述长度的出现进行计数；基于在出现所述差时对所述长度的所述出现的所述计数来生成包括至少一个霍夫曼树的霍夫曼编码；生成一个或多个编码映射，所述一个或多个编码映射包括将所述差和所述长度中的每一个映射到对应霍夫曼前缀码的数组；以及使用所述一个或多个编码映射来对所述多个数中的至少一个数进行编码。在整数的情况下，所述指数包括零位并且针对浮点数，有效数字具有长度。

在至少一个示范性实施例中，在出现所述差时对所述长度的所述出现的所述计数包括递增与所述差相关联的直方图组。所述霍夫曼编码可选地包括针对所述差的直方图的一个霍夫曼树，其中每个叶子具有针对所述长度的直方图的下级霍夫曼树。

在至少一个示范性实施例中，所述编码映射通过遍历多个所述霍夫曼树内的路径来生成，其中每个路径是一个前缀码并且通向存储所述差和所述长度中的一个或多个的一个叶节点。

根据本发明的一个方面，针对压缩浮点数，对所述多个浮点数中的至少一个浮点数进行编码的所述步骤还包括计算针对所述多个浮点数中的所述至少一个浮点数中的每个浮点数计算所述长度和所述差以及从所述一个或多个编码映射检索针对所述差的对应霍夫曼前缀码和针对所述长度的对应霍夫曼前缀码。

根据本发明的一个方面，多核计算机和/或多节点服务器被采用并且系统的多个实例并行操作以独立地对划分的输入的对应部分进行压缩。

有利地，本发明的说明性实施例提供对地震数据和其他数据的改进的无损压缩和解压缩。本发明的这些和其他特征以及优点将从附图和下面的详细描述变得更显而易见。

附图说明

图1图示了根据示范性IEEE 754浮点标准的示范性单精度浮点数；

图2图示了由有理压缩算法的示范性实施例使用的数个示范性数据结构和算法；

图3是图示了根据本发明的一个实施例的有理压缩算法的示范性实施方式的流程图；

图4A图示了由图3的示范性有理压缩算法生成的直方图的示范性直方图；

图4B图示了由图3的示范性有理压缩算法生成的示范性霍夫曼森林；

图5是图示了根据本发明的一个实施例的有理解压缩算法的示范性实施方式的流程图；以及

图6是本发明的至少一个实施例能够被实施在其上的示范性计算机系统的系统图。

具体实施方式

本文中将参考示范性通信、存储和处理设备来描述本发明的说明性实施例。然而，应认识到，本发明不限于与示出的特定说明性配置一起使用。本发明的方面提供用于对诸如整数和浮点数据的数进行有理压缩和解压缩的方法和装置。

根据本发明的一个方面，提供了用于基于数的有理表示来对整数和浮点数进行压缩和解压缩的算法。在至少一个实施例中，该算法提供索引结构以用于使用数本身的特性来编码和解码，避免对附加的数据结构的需要，并且因此改进压缩效率。更具体地，示范性算法将数转换成其有理表示以从该表示提取可压缩的模式。有理表示揭示能够被利用于压缩的编码和解码流程。

所公开的算法特别适合于来源于地震采集或科学实验的数据，因为算法的至少一个实施例专门针对数的集合。如基于本公开将对于本领域技术人员而言显而易见的，尽管本文中使用地震数据来描述 示范性实施例，但是本发明的方面能够被应用到其他形式的数据。

根据本发明的另一方面，使用并行运行在多核计算机和/或多节点服务器上的所公开的算法的多个实例来实现分布式压缩和解压缩。示范性算法作用于数的集合，即，没有顺序的数的序列，使其可扩展用于多个并行运行。

地震数据

石油和天然气公司通常在对给定勘探区进行钻井之前采集并处理来自该区域的地震数据。地震采集包括使用诸如振动器单元、炸药或气枪的源来生成声波，并且然后收集与反射波有关的数据。借助于被称为地震检波器(当采集发生在陆上时)或水下检波器(当采集发生在海上时)的接收器来收集信号。接收器将声振动转换成一般具有从8到32位的数个位的数字样本流。继续以具有恒定持续时间(通常在2与8毫秒之间)的间隔来收集样本，并且通常通过许多接收器同时收集数据。地震数据集能够具有许多兆兆字节(terabyte)的原数据并且它们的处理在地震处理步骤中的各个点处生成其他附加的数据集。

尽管有损压缩算法能够达到高得多的压缩比的事实，但是在地震处理的各个步骤中无损压缩是令人期望的。原始数据必须以原始精度被保存以便避免丢失相关信息。具体地，诸如在盐下区中的复杂地质情况具有非常低的信噪比，其使得具有高数据频率的保存甚至更重要(在有损压缩方法中，高频率通常被衰减，使得能够获得更高的压缩比)。因此，确保采用的压缩方法是无损的常常是重要的。

地质处理工作流程通常与修改原数据的各个步骤相对应，并且在每个步骤处创建新地震数据文件。取决于阶段和利用的处理技术，产生的文件的大小能够与原始文件一样大。发现减少由这些大的数据文件占据的大小并高效地将其存储的方式是需要被解决的问题。

因此，对地震数据的存储和传输要求无损压缩。对实现高压缩比的算法的创建对于节省存储和传输时间是重要的。

因为地震数据文件可以是非常大的，所以对它们进行压缩的时间 可以是非常长的，有时花费许多天来获得好的压缩比。以这种方式，将用于获得良好压缩比的时间减少一定数量级可以是与工业非常相关的。

石油和天然气公司常常是全球公司并且对地震数据的解读是其中地球物理学家和地理学家常常必须跨距离合作的过程。对这些数据的高效传输对于使该过程有成效是必要的。好的压缩比对于在传输期间节省时间是重要的，尤其是在有必要利用有限带宽并且没有任何信息损失的情况下发送数据时。

在计算机系统上，数据通常是位(二进制数)序列，其中，每个位是2为底的数(即，二进制0或二进制1)。位序列可以表示例如数、文本、图像、声音或任何种类的信息。信息通过诸如磁带、硬盘和固态驱动器的数据存储设备的使用保持在计算机系统上。

在石油和天然气工业中，地震数据常常通过使用由勘探地球物理学家协会(SEG)开发的用于存储地震数据的若干标准之一而被存储为地震道。最常用的格式是SEG Y。在最常见类型的SEG Y文件内，地震道由32位浮点数的序列表示。为了利用该类型的数据在不丢失任何信息的情况下工作，特别注意是必要的。

因此，地震样本数据常常被表示为浮点数。典型格式是IBM和IEEE 754单精度浮点表示，其指定如何将实数存储在32位中。这些表示保留一个位来指示该数的符号，而其他31位被拆分成以特定底数的指数和有效数字，使得实数R被计算为：

R＝(-1)^符号x有效数字x b^指数

IBM浮点数格式与IEEE 754格式之间的主要差别是为每个部分保留的位数和指数的底数b。本文提出的示范性算法已经针对IEEE 754格式被设计，因为其常常在现代计算中被采用，但是如对于本领域技术人员而言将显而易见的，这些算法能够被推广到其他格式。

图1图示了根据IEEE 754浮点标准的示范性单精度浮点数100。如图1所示，示范性单精度浮点数100使用一位用于符号110，八位用于底数为2的指数120，以及23位用于归一化的有效数字130， 意味着实数R被计算为：

R＝(-1)^符号x 1.有效数字x 2^指数。

当整数类型表示整数时，浮点数类型表示具有小数部分的数。地震数据采集和科学数据勘探通常具有这两种类型的数作为它们的核心二进制数据。附加地，主要来自调查、仿真和实验的数据消耗大量存储空间。

在地震数据采集或科学仿真的领域中，无损压缩的选项可能是更有吸引力的或由于产生数据的成本甚至是要求。一个策略是丢弃位序列的意义，即，无论它们是数还是不是数，并且实现通用无损压缩算法。在该策略中存在两个主要缺点。首先，对给定文件进行压缩和解压缩的时间性能可能受到影响，因为通用算法必须在没有关于数据的任何先验知识的情况下花费时间来搜索可压缩模式。第二，精简效率或压缩比也可能由于未找到文件中的最好可压缩模式而受到影响。这些缺点对将通用无损压缩算法用于地震或科学数据带来挑战。

为了克服具有固定长度的位的数的集合内的存储空间的浪费，并且不损失关于每个数的信息，本发明的方面定义一种利用减小的长度对每个数进行编码和解码的算法。结果是包括具有可变长度的数的压缩集合，其能够被解压缩成原始长度。

下面的讨论被划分成三个部分：对在计算机系统上对数的表示的解释；对有理数和其表示以及与其他数的相互作用的描述；以及对本文中使用的基本数据结构和算法的讨论。

数的表示

整数通常由32位的序列表示，其中在有符号整数的情况下，第一位是符号位，指示其是正整数还是负整数，并且剩余位是底数为2的整数本身。无符号整数没有符号位，使用第一位作为用于数本身的多一位。除了符号位，出现在序列的左边的任何前导零不是有效位，因为它们能够由于相同数值而被省略。浮点数类型100允许通过将指数120插入到通常具有相同的32位长度的序列中来表达数的 小数部分。第二位到第九位通常将该指数120表示为底数为2的最小指数和最大指数之间的整数。指数120可以在如下的意义上被偏置，指数120减去固定数以表示负指数和正指数。127的偏置意味着指数从-127到128变化。第十位到该序列的末尾通常表示小数，还称为尾数或有效数字130，为浮点数100的部分。小数130可以是以归一化形式的，在这种情况下，最大有效位被隐藏在序列中，因为它总是二进制1。出现在序列的右边的任何尾随零不是有效位，因为它们能够由于相同数值而被省略。

整数和浮点数可以通过不同规格来表示并且可以具有不同长度的位。存在指导对计算机上的数进行定义的若干国际标准，并且计算机系统可以甚至使用除了二进制(底数为2)以外的底数。如对于本领域技术人员而言将显而易见的，尽管针对整数和浮点数给出的解释用作本文中使用的概念的基线，但是所公开的有理压缩算法独立于数的规格、长度和底数而作用。

有理数及其表示

示范性有理压缩算法通过由原始数的有理表示改变其表示来作用，以更高效地对该数进行压缩。有理数由涉及整数分子p和整数分母q的比值表征如下：

p/q。

其中q≠0。当q＝1时，有理数是整数。浮点数f由不包括尾随零的有效数字s 130、底数b和指数e定义如下：

f＝s·b^e。

其中，在二进制计算机系统中，b＝2，并且有效数字130和指数120两者都是位序列。如果s是整数，则f的有理表示被表达如下：

$\frac{s}{2^{-e}}.$

其中，分母2^-e在2的负幂的情况下上升为乘以分子。f的该有理表示暗示小数为零，即，有效数字s 130在其(有效数字位序列的)长度l为零时仅仅是整数，并且因此分子变成隐藏的归一化位：1。通过定义，针对归一化浮点数，作为数的小数部分的有效数字s 130是 在二进制点的右边的没有尾随零的位序列。

具有零小数部分的浮点数的有理表示排除大多数数，致使其无用。示范性有理压缩算法针对易受到压缩的浮点数定义分子和分母两者。分子通过将有效数字s 130乘以2的有效数字序列的长度l的幂的结果来定义如下：

p＝s·2^l。

换言之，将s改写为整数并将小数l位移动到右边等价于将其乘以2^l。除了小数部分，符号位110被连接到有效数字序列的开头以使s为有符号整数。分母通过将2^-e乘以2^l来定义以补偿插入在分子上的乘法，即：

q＝2^l-e。

q和p的这些定义用于指导在示范性有理压缩算法的步骤内对浮点数的编码和解码。以其有理表示的最终浮点数被表达如下：

$f=\frac{s\·2^l}{2^{l-e}}.$

注意该表示的对于对数进行编码和解码有用的两个属性。第一，幂总是以二为底数的(或以数为底数的)，并且因此，数二(或底数)能够被忽略。第二，变量l携带必须读取多少位以获得s的信息。该信息对于恢复具有可变长度的s值的序列有用。这些属性导致有理压缩算法的示范性实施例集中于在任何浮点数中呈现的(l-e)和l值。

数据结构和算法

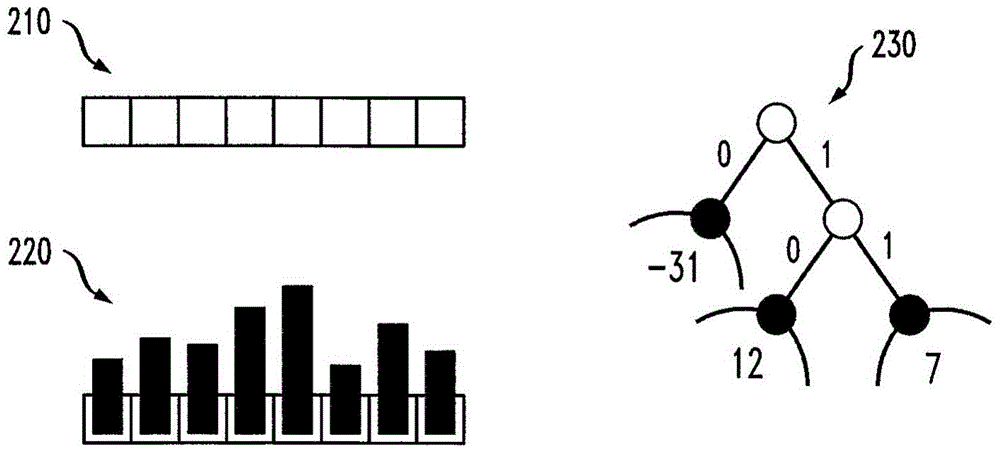
图2图示了由有理压缩算法的示范性实施例使用的数个示范性数据结构和算法。如图2所示，有理压缩算法的示范性实施例采用一个或多个数组210和直方图220。数组210是利用数组内部的对应位置来存储值的数据结构。直方图220是其中值是频率的数组，对于对每个元素在集合中的出现进行计数有用。在图2的示范性实施例中，数组210具有8个位置并且用于通过直方图220存储8个元素在集合中的出现，其中，数组内的条的大小表示出现的次数。

图2还图示了二叉树230，其是具有两个内部节点(白色开放圆 圈)和三个叶节点(黑色闭合圆圈)的霍夫曼(Huffman)树。二叉树230是用于进行映射的数据结构，其对于将键映射到值有用。霍夫曼树是二叉树，其键是集合中的每个值或元素的最小前缀码。码是表示特定值的位序列，一般具有比值本身更少的位。前缀码是特定类型的码，其前缀、即初始序列不在任何其他码中重复。霍夫曼编码算法接收要编码的元素的频率的直方图220作为输入，并且返回与在直方图220中呈现的分布相对应的霍夫曼树作为输出。霍夫曼编码和树一般用于无损压缩。

示范性二叉树230利用代码0对数-31进行编码，利用代码10对数12进行编码并且利用代码11对数7进行编码。代码序列由以已知方式从树中的一个节点到另一节点的路径表示。

对于图2中示出的示范性数据结构和算法的更详细讨论参见例如T.H.Cormen等人的由MIT出版社出版的“Introduction to Algorithms”(ISBN 978-0262033848)，通过引用将其并入本文中。

有理压缩算法

在至少一个实施例中，示范性有理压缩算法包括压缩模式和解压缩模式。

图3是图示根据本发明的一个实施例的有理压缩算法300的示范性实施方式的流程图。示范性有理压缩算法300接收存储浮点数的集合的文件作为输入并且返回以压缩格式存储相同集合的压缩文件作为输出。

如图3所示，示范性读取阈值电压调节过程300首先在步骤310期间计算直方图的直方图(hh)，其是(l-e)出现的一个直方图，其中每个元素是l出现的另一直方图。下面结合图4A进一步讨论示范性直方图的直方图(hh)400。

在步骤320期间，示范性读取阈值电压调节过程300构建hh的霍夫曼森林(hf)，其是针对(l-e)的直方图的一个霍夫曼树，其中每个叶子具有针对l的直方图的下级霍夫曼树。下面结合图4B进一步讨论hh的示范性霍夫曼森林(hf)450。

在步骤330期间，示范性读取阈值电压调节过程300构建编码映射(em)，其是将每个(l-e)和l映射到其对应的霍夫曼前缀码中的一个数组。编码映射em是针对具有针对每个l值的前缀码的另一下级数组的每个(l-e)值的前缀码的数组。这些数组通过遍历在(在步骤320期间生成的并且如下面结合图4B进一步讨论的)hf中的所有霍夫曼树内的所有可能路径来构建，其中每个路径是一个前缀码并且在主霍夫曼树的情况下(460)通向存储(l-e)的一个叶节点或者在下级霍夫曼树的情况下(470)通向存储l的一个叶节点。编码映射em包含在浮点数的输入集合中出现的所有可能的(l-e)和l值的码序列。

在步骤340期间，示范性读取阈值电压调节过程300使用编码映射(em)对每个浮点数进行编码，如下面结合标题为“将浮点数编码成压缩位”的章节进一步讨论的。

图4A图示了在步骤310期间由示范性有理压缩算法300生成的示范性直方图的直方图(hh)400。如图4A所示，示范性直方图的直方图(hh)400是(l-e)出现的一个直方图410，其中每个元素是l出现的另一直方图420-i。主直方图410利用对l的出现进行计数的另一直方图420对(l-e)的出现进行计数。更具体地，针对输入集合中的每个唯一的浮点数f，从f计算l和(l-e)并递增hh[l-e][l],hh[l-e][l]是l在(l-e)的直方图410内部的其对应的直方图420中的出现。该递增仅仅影响一个直方图420，在出现(l-e)时对l的出现进行计数。另一方面，(l-e)的出现通过对在其内部直方图中l的所有出现的求加和来计数。

主直方图410的范围是(l-e)值加两个特殊位置的可能范围。一个特殊位置针对无效数，例如无穷大和NaN(非数字)，其具有必须被保留的特殊位序列，而另一特殊位置针对数零，其小数未被归一化并且具有长度零，即l＝0。包含在主直方图410的每个位置内部的每个内部直方图420的范围是l的可能范围。针对具有1个符号位、用于指数的8位和用于小数部分的23位的32位浮点数，主直 方图410的范围是281并且每个直方图420的范围是23。

图4B图示了在步骤320期间由示范性有理压缩算法300生成的hh的示范性霍夫曼森林(hf)450。如图4B所示，针对(l-e)出现的主直方图410构建一个霍夫曼树460，并且针对l出现的每个内部直方图构建一个下级霍夫曼树470-i。这些霍夫曼树460、470形成霍夫曼森林hf 450，其对于压缩和解压缩两者有用。霍夫曼森林450被存储在压缩输出文件的开头。霍夫曼森林(hf)450还在本文中被称为霍夫曼编码。

将浮点数编码成压缩位

如以上指示的，在步骤340期间，示范性有理压缩算法300使用在步骤330期间生成的编码映射将每个浮点数f编码成压缩位序列。更具体地，针对输入中的每个f，从f计算l和(l-e)并从em检索针对(l-e)的前缀码和针对l的前缀码。针对f产生的位序列包括：第一，(l-e)前缀码；第二，l前缀码；以及第三，从f提取的有效数字序列s。归一化位不存在并且序列s的最后一位从产生的序列被排除，因为其总是1。通过定义，序列s包括在二进制点的右边的没有尾随零的所有有效数字位。该产生的序列在其长度小于用于表示浮点数f的原始位序列时被认为被压缩。输入集合被完全编码并被存储在压缩输出文件中的霍夫曼森林hf之后。

解压缩

图5是根据本发明的一个实施例的有理解压缩算法500的示范性实施方式的流程图。一般地，示范性有理解压缩算法接收以压缩格式存储霍夫曼森林450和浮点数的集合的压缩文件作为输入，并且返回与在压缩之前的原始文件完全相同的未压缩文件作为输出。

如图5所示，示范性有理解压缩算法500首先在步骤510期间从压缩输入文件读取并重新构建霍夫曼森林hf 450。霍夫曼森林450包含用于对针对在压缩集合中出现的(l-e)和l值的所有可能的前缀码进行解码的必要信息。hf中的第一霍夫曼树460是(l-e)出现的直方图的主树，而hf中的所有其他霍夫曼树470是l出现的直方 图的下级树。每个下级霍夫曼树470的次序与(l-e)的主直方图410的次序相匹配，即是l的内部直方图的相同次序。在步骤510期间，仅仅霍夫曼森林hf 450被重新构建，解压缩不需要编码映射或直方图400。

此后，示范性有理解压缩算法500在步骤520期间使用霍夫曼森林hf 450将每个压缩位序列解码成浮点数。更具体地，压缩输入文件在霍夫曼森林450之后被读取作为位序列，并且针对每个位，对主霍夫曼树进行遍历直到到达叶节点。叶节点包含与当前浮点数f相对应的(l-e)值。针对对应的下级霍夫曼树重复该过程，对对应的下级霍夫曼树进行遍历直到到达叶节点。该第二叶节点包含当前数f的l值，其允许读取下个l位以构建浮点数f的有效数字序列s。利用s、l和(l-e)，浮点数f使用其有理表示被恢复：f＝s·2^l/2^l-e。输入压缩集合被完全解码并被写入未压缩输出文件中。

变型

在一个变型中，算法被定制用于整数，其中有理表示具有等于整数本身的分子并且分母等于1。整数的输入集合仅仅使用每个整数的位的长度来被压缩。该长度可以与浮点数的长度l类似地被使用，以使得整数能够在没有前导零并且排除第一位1的情况下被恢复。然而，整数的长度不会对恢复原始整数做出贡献，因为其没有小数部分。霍夫曼森林450减少为仅仅对整数的长度进行编码的一个霍夫曼树460，并且算法的其他部分保持相同。在整数的情况下，长度具有整数的有效位的意义，而在浮点数的情况下，长度具有有效数字的意义。

在另一变型中，有理压缩算法300适合于对整数和浮点数的混合集合起作用，或者对不同规格的数起作用。策略是增加或减少主直方图410或内部直方图420中的位置以支持这些不同的数。例如，在固定集合的情况下，除了在浮点数的(l-e)值的直方图410中的两个特殊位置，多一个特殊位置可以用于整数值。还增加l的内部直方图420的范围以支持浮点数的有效数字的长度和整数的长度两者。 另一示例是考虑具有表示算数的除以零的结果的特殊序列的浮点数。这还可以向主直方图添加位置，类似于无穷大和NaN(非数字)表示。霍夫曼森林450使用这些调整的直方图来构建，并且算法的其他部分保持相同。

第三变型利用直方图的不同组合或利用仅仅一个直方图来代替直方图400。例如，主直方图410可以对仅仅从每个浮点数f提取的指数e而非(l-e)值的出现进行计数，并且内部直方图可以继续对l的出现进行计数。霍夫曼森林450使用这些直方图400来构建，并且编码可以继续保留有效数字序列s。解码仍然起作用，因为数f可以仍然从s、l和e被恢复。该策略还可以被颠倒，其中主直方图410对l的出现进行计数，而内部直方图420对e的出现进行计数。另一示例是利用对l和e的对的出现进行计数的仅仅一个直方图来代替直方图的直方图400。这将霍夫曼森林450减少为对l和e的对进行编码的仅仅一个霍夫曼树，并且算法300的其他部分保持相同。

在又一变型中，另一无损压缩策略被添加到有效数字序列s，而非将序列保留在压缩文件中。一个策略可以搜索原始有效数字位序列中的可重复子序列并且可以创建这些子序列的词典。重复子序列由词典的索引码来代替，其包含每个子序列的仅仅一个实例。在索引码和词典减少编码子序列的长度的情况下压缩是高效的。词典可以在霍夫曼森林之后被存储并且索引码可以代替对应的子序列。

另一变型通过不同的编码策略来代替霍夫曼森林450。例如，可以针对l和e值两者来构建词典。该字典可以是使用要压缩的数的集合的先前知识的静态词典，或者随着集合被压缩而调整的动态词典，或者两者的组合。数的编码和解码与使用霍夫曼森林类似。

附加的变型使有理压缩算法300适合于多核计算机或多节点服务器。多核计算机系统包括能够并行执行计算的数个处理单元，每个处理单元如同可分离的计算机系统。多节点服务器是具有数个相互连接的计算机系统的分布式环境。使算法并行化的一个策略是将输入集合划分成针对每个计算机系统一个的具有相似大小的集合， 并运行算法的若干实例。

结论

本文中参考根据本发明的实施例的方法、装置(系统)和计算机程序产品的流程图图示和/或方框图来描述本发明的方面。将会认识到，流程图图示和/或方框图的每个框以及流程图图示和/或方框图中的框的组合能够通过计算机程序指令来实施。这些计算机程序指令可以被提供给通用计算机、专用计算机或其他可编程数据处理装置的处理器以产生一种机器，使得经由计算机或其他可编程数据处理装置的处理器运行的指令创建用于实施流程图和/或一个或多个方框图框中指定的功能/动作的部件。

如在本文中进一步描述的，这样的计算机程序指令还可以被存储在计算机可读介质中，其能够引导计算机、其他可编程数据处理装置或其他设备以特定方式工作，使得存储在计算机可读介质中的指令产生包括实施在流程图和/或一个或多个方框图框中指定的功能/动作的指令的一款制品。因此，如下面进一步详细描述的，本发明的至少一个实施例包括有形地体现计算机可读指令的一款制品，所述计算机可读指令当被实施时使得计算机执行本文中描述的技术。如本文中使用的，一款制品、计算机程序产品或计算机可读存储介质不应被解释为瞬态信号，诸如电磁波。

计算机程序指令还可以被加载到计算机或其他设备上以使一系列操作步骤被执行在计算机、其他可编程装置或其他设备上，以产生计算机实施的过程，使得运行在计算机或其他可编程装置上的指令提供用于实施在流程图和/或一个或多个方框图框中指定的功能/动作的过程。

在附图中的流程图和方框图图示了根据本发明的各种实施例的系统、方法和计算机程序产品的可能实施方式的体系结构、功能和操作。就这点而言，流程图或方框图中的每个框可以表示代码的模块、组件、片段或部分，其包括用于实施指定的逻辑功能的至少一个可执行指令。应当指出，框中指出的功能可以以附图中指出的顺 序以外的顺序出现。

因此，本文中描述的技术能够包括提供一种系统，其中所述系统包括不同的软件模块，每个软件模块被体现在有形计算机可读可记录存储介质上(例如，所有模块被体现在相同的介质上，或者每个模块被体现在不同的介质上)。例如，模块能够运行在硬件处理器上，并且本文中详细描述的技术能够使用运行在硬件处理器上的系统的不同软件模块来执行。

附加地，本文中详细描述的技术还能够经由计算机程序产品来实施，所述计算机程序产品包括存储在数据处理系统中的计算机可读存储介质中的计算机可用程序代码，其中计算机可用程序代码通过网络从远程数据处理系统被下载。计算机程序产品还可以包括，例如，存储在服务器数据处理系统中的计算机可读存储介质中的计算机可用程序代码，其中计算机可用程序代码通过网络被下载到远程数据处理系统以用于与远程系统一起在计算机可读存储介质中使用。

如本领域技术人员将认识到的，本发明的方面可以采取完全硬件实施例、完全软件实施例(包括固件、常驻软件、微代码等)或将软件和硬件方面进行组合的实施例的形式，其全部可以在本文中被一般地称为“模块”和“系统”。

本发明的方面或其元件能够以包括存储器和至少一个处理器的装置的形式来实施，所述至少一个处理器被耦合到所述存储器并且可操作为执行本文中描述的技术。此外，如本文中描述的，本发明的方面可以采取计算机程序产品的形式，所述计算机程序产品被体现在具有计算机可读程序代码体现在其上的计算机可读介质中。

通过举例的方式，本发明的方面可以利用运行在通用计算机上的软件。图6是本发明的至少一个实施例能够被实施在其上的示范性计算机系统的系统图。如图6中描绘的，示例实施方式采用例如处理器602、存储器604以及例如由显示器606和键盘608形成的输入/输出接口。如本文中使用的术语“处理器”包括任何处理设备，诸 如举例而言，包括中央处理单元(CPU)和/或处理电路的其他形式的处理设备。术语“存储器”包括与处理器或CPU相关联的存储器，诸如举例而言，随机存取存储器(RAM)、只读存储器(ROM)、固定存储器设备(例如，硬盘驱动器)、可拆卸存储设备(例如，磁盘)、快闪存储器等等。另外，如本文中使用的短语“输入/输出接口”包括用于向处理单元输入数据的机构(例如，鼠标)和用于提供与处理单元相关联的结果的机构(例如，打印机)。

处理器602、存储器604以及诸如显示器606和键盘608的输入/输出接口能够例如经由作为数据处理单元612的部分的总线610相互连接。经由总线610的适当的相互连接还能够被提供给网络接口614(例如网络卡)和介质接口616(诸如磁盘或紧凑盘只读存储器(CD-ROM)驱动器)，所述网络接口614能够被提供以与计算机网络接口，所述介质接口能够被提供以与介质618接口。

因此，包括用于执行本文中详细描述的技术的指令或代码的计算机软件能够被存储在相关联的存储设备(例如，ROM、固定存储器或可拆卸存储器)中并且当准备好被利用时部分地或整体地被下载(例如，到RAM中)并且由CPU来实施。这样的软件能够包括固件、常驻软件、微代码等等。

如以上指出的，适合于存储和/或执行程序代码的数据处理系统包括通过系统总线610直接或间接耦合到存储器元件604的至少一个处理器602。存储器元件能够包括在程序代码的实际实施期间采用的本地存储器、大容量存储器以及高速缓存存储器，高速缓存存储器提供对至少一些程序代码的临时存储以便减少在实施期间必须从大容量存储器检索代码的次数。同样，诸如键盘608、显示器606和定点设备的输入/输出(I/O)设备能够(例如经由总线610)直接地或通过中介I/O控制器被耦合到系统。

诸如网络接口614的网络适配器(例如，调制解调器、线缆调制解调器或以太网卡)还能够被耦合到系统以使得数据处理系统能够通过中介私有网络或公共网络被耦合到其他数据处理系统或远程 打印机或存储设备。

如本文中使用的，“服务器”包括运行服务器程序的物理数据处理系统(诸如如图6中描绘的系统612)。将理解，这样的物理服务器可以包括或可以不包括显示器和键盘。

如指出的，本发明的至少一个实施例能够采取计算机程序产品的形式，所述计算机程序产品被体现在具有计算机可读程序代码体现在其上的计算机可读介质中。如将认识到的，计算机可读介质的任何组合可以被利用。计算机可读介质能够包括计算机可读信号介质或计算机可读存储介质。计算机可读存储介质可以是，例如但不限于，电子的、磁的、光的、电磁的、红外的或半导体系统、装置或设备或者前面的任何适当的组合。示例包括具有一条或多条线的电连接、便携式计算机磁盘、硬盘、RAM、ROM、可擦可编程只读存储器(EPROM)、快闪存储器、光纤、便携式CD-ROM、光存储设备、磁存储设备和/或前面的任何适当的组合。更一般地，计算机可读存储介质可以是能够包含或存储用于由指令执行系统、装置或设备或结合指令执行系统、装置或设备使用的程序的任何有形介质。

附加地，计算机可读信号介质可以包括具有计算机可读程序代码体现在其中的传播的数据信号，例如在基带中或作为载波的一部分。这样的传播信号可以采取诸如举例而言电磁、光学或其适当的组合的各种形式中的任何形式。更一般地，计算机可读信号介质可以是任何计算机可读介质，其不是计算机可读存储介质并且其能够通信、传播或传输用于由指令执行系统、装置或设备或结合指令执行系统、装置或设备使用的程序。

体现在计算机可读介质上的程序代码能够使用诸如举例而言无线、有线、光纤线缆、射频(RF)和/或前面的适当的组合的合适的介质来传输。用于执行根据本发明的一个或多个实施例的操作的计算机程序代码能够以包括面向对象编程语言和传统过程式编程语言的至少一个编程语言来编写。程序代码可以完全在用户的计算机上、部分在用户的计算机上、作为独立软件包、部分在用户的计算机上 并且部分在远程计算机上、或者完全在远程计算机或服务器上来运行。在后一情形下，远程计算机可以通过包括局域网(LAN)或广域网(WAN)的任何类型的网络被连接到用户的计算机，或者可以(例如，通过使用互联网服务提供商的互联网)进行与外部计算机的连接。

鉴于以上描述，应当理解本文中图示的部件能够被实施在各种形式的硬件、软件或其组合中，例如专用集成电路(ASIC)、功能电路、具有相关联的存储器的合适地编程的通用数字计算机等等。

本文中使用的术语仅仅出于描述特定实施例的目的并且不旨在为对本发明的限制。例如，单数形式的“一”、“一个”和“所述”旨在也包括复数形式，除非另行清楚指示。还将理解，如本文中使用的术语“包括”和/或“包含”指定陈述的特征、整数、步骤、操作、元件和/或部件的存在，但不排除另一特征、整数、步骤、操作、元件、部件和/或它们的组的存在或添加。附加地，对应的结构、材料、动作和权利要求书中的所有部件或步骤加功能元件的等价物旨在包括用于与如特别要求保护的其他要求保护的元件相结合来执行功能的任何结构、材料或动作。

此外，应当再次强调，本发明的上述实施例仅仅出于说明的目的而被呈现。可以使用许多变型和其他备选实施例。例如，该技术适用于能够从对数据的改进的有理压缩获益的各种其他类型的通信系统、存储系统和处理设备。因此，本文中详细描述的系统和设备元件的特定说明性配置能够在其他实施例中被改变。所附权利要求书的范围内的这些实施例和许多其他备选实施例对于本领域技术人员而言将是显而易见的。