一种数据处理方法及装置与流程

本发明涉及编码解码技术领域，具体而言，涉及一种数据处理方法及装置。

背景技术：

LDPC码是一种逼近香农限的，易实现和系统复杂度低的优秀的线性纠错码，它是由Robert Gallager博士于1963年提出的一类具有稀疏校验矩阵的线性分组码，LDPC码不仅有逼近香农限的良好性能，而且译码复杂度较低,结构灵活，是近年信道编码领域的研究热点。目前已广泛应用于深空通信、光纤通信、卫星数字视频和音频广播等领域。LDPC码已成为第四代通信系统(4G)强有力的竞争者，而基于LDPC码的编码方案已经被下一代卫星数字视频广播标准DVB-S2采纳。

发明人发现，在LDPC码矩阵的译码解码过程中，只能通过串行解码的方式进行，如果LDPC码矩阵中的编码数量较多，串行解码的方式就会耗费大量的时间，解码效率低，占用较多的系统资源。

技术实现要素：

有鉴于此，本发明提供了一种数据处理方法，可以并行实现对LDPC编码矩阵的解码，解码效率高。

本发明提供的技术方案如下：

一种数据处理方法，用于对低密度奇偶校验码译码，低密度奇偶校验码的校验矩阵包括左子矩阵和右子矩阵，该方法包括：

对所述左子矩阵和右子矩阵进行行变换，对所述右子矩阵进行列变换，将所述校验矩阵转换为包含多个n阶方阵的第一矩阵；

将所述第一矩阵一维化以形成线性数据结构，从所述第一矩阵中选取所有有效元个数为n的整数倍的循环矩阵，记录所述循环矩阵在所述第一矩阵中的行数、列数和初始移位位置；

同时并行提取多个所述循环矩阵，根据所述循环矩阵在所述第一矩阵中的行数、列数和初始移位位置，确定所述第一矩阵。

进一步地，所述将所述第一矩阵一维化以形成线性数据结构的步骤包括：

采用折中分层方式和最小化迭代次数，以减少总操作数。

进一步地，所述校验矩阵的数据表示采用数据定点化表示，具体为将32比特单精度浮点数转换为8比特整数。

进一步地，所述校验矩阵的数据表示采用数据定点化表示，具体为：

将归一化的输入数据利用第一函数缩减运算到-127至127，所述缩减运算过程中采用饱和操作以防止所述8比特整数溢出。

进一步地，在确定所述第一矩阵的步骤中，采用多个并发线程进行确定，具体为：

将所述第一矩阵中的线程块映射为一个校验矩阵包含多个循环矩阵的形式，将线程映射为一个单一非叠加的循环矩阵包含m个有效元的形式，m为360。

进一步地，所述低密度奇偶校验码为DVB-S2内码或前置交织操作的LDPC码。

进一步地，所述数据处理方法采用图形处理器GPU实现。

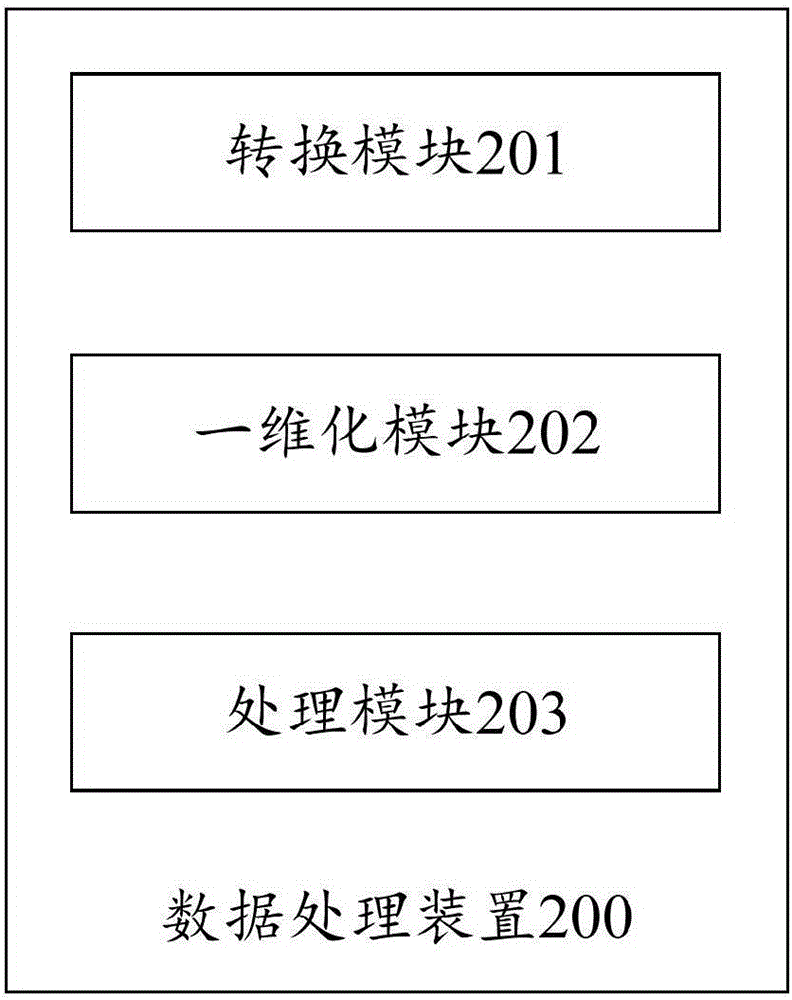
本申请还提供了一种数据处理装置，用于对低密度奇偶校验码译码，低密度奇偶校验码的校验矩阵包括左子矩阵和右子矩阵，该装置包括：

转换模块，用于对所述左子矩阵和右子矩阵进行行变换，对所述右子矩阵进行列变换，将所述校验矩阵转换为包含多个n阶方阵的第一矩阵；

一维化模块，用于将所述第一矩阵一维化以形成线性数据结构，从所述第一矩阵中选取所有有效元个数为n的整数倍的循环矩阵，记录所述循环矩阵在所述第一矩阵中的行数、列数和初始移位位置；

处理模块，用于同时并行提取多个所述循环矩阵，根据所述循环矩阵在所述第一矩阵中的行数、列数和初始移位位置，确定所述第一矩阵。

进一步地，所述一维化模块具体用于采用折中分层方式和最小化迭代次数，以减少总操作数。

进一步地，所述校验矩阵的数据表示采用数据定点化表示，具体为将32比特单精度浮点数转换为8比特整数。

利用本发明提供的数据处理方法，在对低密度奇偶校验码矩阵进行解码过程中，通过行变换将低密度奇偶校验码矩阵转换为包含多个n阶方阵的形式，并通过矩阵一维化记录保存数据内容非零的n阶方阵的行数、列数和各自的数据内容。从而在解码时，可以同时并行的提取多个数据内容非零的n阶方阵，通过其行数、列数和数据内容确定低密度奇偶校验码矩阵的数据内容，实现解码。解码过程中，无需对矩阵中所有的数据进行处理，只需处理数据内容非零的数据，数据处理量更少，并且一维化后可以实现并行处理，也不会发生干扰和编码信息的损失。解码速度更快，解码效率更高，可以充分利用图形处理器的并行数据处理能力，提高设备的利用率。

为使本发明的上述目的、特征和优点能更明显易懂，下文特举较佳实施例，并配合所附附图，作详细说明如下。

附图说明

为了更清楚地说明本发明实施例的技术方案，下面将对实施例中所需要使用的附图作简单地介绍，应当理解，以下附图仅示出了本发明的某些实施例，因此不应被看作是对范围的限定，对于本领域普通技术人员来讲，在不付出创造性劳动的前提下，还可以根据这些附图获得其他相关的附图。

图1为本发明实施例提供的一种数据处理方法的流程示意图。

图2为本发明实施例提供的一种数据处理装置的功能模块示意图。

具体实施方式

下面将结合本发明实施例中附图，对本发明实施例中的技术方案进行清楚、完整地描述，显然，所描述的实施例仅仅是本发明一部分实施例，而不是全部的实施例。通常在此处附图中描述和示出的本发明实施例的组件可以以各种不同的配置来布置和设计。因此，以下对在附图中提供的本发明的实施例的详细描述并非旨在限制要求保护的本发明的范围，而是仅仅表示本发明的选定实施例。基于本发明的实施例，本领域技术人员在没有做出创造性劳动的前提下所获得的所有其他实施例，都属于本发明保护的范围。

应注意到：相似的标号和字母在下面的附图中表示类似项，因此，一旦某一项在一个附图中被定义，则在随后的附图中不需要对其进行进一步定义和解释。同时，在本发明的描述中，术语“第一”、“第二”等仅用于区分描述，而不能理解为指示或暗示相对重要性。

低密度奇偶校验码(Low Density Parity Check Code，LDPC)，是一种非常常见的编码方式，LDPC码具有巨大的应用潜力，在深空通信、光纤通信、卫星数字视频、数字水印、磁/光/全息存储、移动和固定无线通信、电缆调制/解调器和数字用户线(DSL)中得到广泛应用。

在数据处理过程中，通过低密度奇偶校验码矩阵实现编码的传递和解码。现有技术中，对低密度奇偶校验码矩阵解码时是串行执行的。需要将低密度奇偶校验码矩阵中的所有数据元素进行保存并处理。

由于低密度奇偶校验码矩阵可以是稀疏矩阵，稀疏矩阵中包含有大量的零元素，在进行解码时，对零元素的处理过程是没有实际意义的，但由于零元素的数量庞大，使得低密度奇偶校验码矩阵的解码过程效率较低。

当使用图形处理器(Graphics Processing Unit，GPU)对低密度奇偶校验码矩阵进行解码时，由于只能串行执行解码过程，不能充分利用GPU的并行处理能力，降低了GPU的使用效率，造成了系统资源的浪费。

有鉴于此，本申请实施例提供了一种数据处理方法，用于对低密度奇偶校验码矩阵解码，如图1所示，该方法包括：

步骤101，对所述左子矩阵和右子矩阵进行行变换，对所述右子矩阵进行列变换，将所述校验矩阵转换为包含多个n阶方阵的第一矩阵。

本申请实施例中的低密度奇偶校验码矩阵左子矩阵和右子矩阵，并且左子矩阵和右子矩阵都为稀疏矩阵，矩阵中数值为0的元素的数量要远远多于非零元素的数量。本申请中对左子矩阵和右子矩阵进行行变换，并对右子矩阵进行列变换，将变量节点信息码元矩阵转换为包含多个n阶方阵的形式。经过行列变换后的校验矩阵仍然是稀疏矩阵，但如果从n阶方阵的维度分析该校验矩阵，其复杂程度得到了一定程度的简化。

本申请实施例中，经过转换后的低密度奇偶校验码矩阵为第一矩阵。在第一矩阵中，既包括数据内容为零的n阶方阵，也包括数据内容非零的n阶方阵。

步骤102，将所述第一矩阵一维化以形成线性数据结构，从所述第一矩阵中选取所有有效元个数为n的整数倍的循环矩阵，记录所述循环矩阵在所述第一矩阵中的行数、列数和初始移位位置。

具体的，在对第一矩阵进行一维化的过程中可以采用折中分层方式和最小化迭代次数，以减少总操作数。

以2/3码为例，可以按循环矩阵的大小(360)为单位进行划分，使校验矩阵天然地形成一个15*45的宏矩阵，一行对应一层。

其中，分层译码Layered decoding计算过程为：

q_m,n[k]＝q_n[k*G+g-1]-r_m,n[k-1]

$r_{m,n}\[k\]=sign(q_{m,n}\[k\])*\mathrm{\β}*\underset{j\∈N\left(m\right)}{\Π}sign(q_{m,j}\[k\])*\underset{j\∈N\left(m\right)\backslash n}{\min }\left(\right|q_{m,j}\[k\]\left|\right)$

q_n[k*G+g]＝q_n[k*G+g-1]+r_m,n[k]-r_m,n[k-1]

令k为迭代索引，g为层索引，G为层数，则层操作如上式所示。q_n被初始化为channel info，并最终作为符号判决的依据输出。对比现有算法的性能结果可知，在性能接近的情况下，分层译码layered decoding算法的迭代次数减半。

在对低密度奇偶校验码矩阵进行转换后，其总体数据量没有发生变化，如果直接对转换后得到的第一矩阵进行解码，解码运算量与直接对低密度奇偶校验码矩阵解码相比并没有显著的降低。在本申请实施例中，进一步的对第一矩阵进行了一维化的操作。

即只对数据内容非零的n阶方阵进行保存，将数据内容非零的n阶方阵的在第一矩阵中的行数、列数和具体的数据内容进行保存。由于低密度奇偶校验码矩阵是稀疏矩阵，其转换后得到的第一矩阵也是稀疏矩阵，第一矩阵中数据内容非零的n阶方阵的数量要远远少于数据内容为零的n阶方阵的数量。因此，仅仅保存数据内容非零的n阶方阵的行数、列数、数据内容等参数的运算量要远远小于保存整个低密度奇偶校验码矩阵的运算量，也要远远小于保存整个第一矩阵的运算量。实现了将二维的第一矩阵转换为一维的数据。

步骤103，同时并行提取多个所述循环矩阵，根据所述循环矩阵在所述第一矩阵中的行数、列数和初始移位位置，确定所述第一矩阵。

在本申请实施例中，所述校验矩阵的数据表示采用数据定点化表示包括：将32比特单精度浮点数转换为8比特整数。并且将归一化的输入数据利用第一函数缩减运算到-127至127，所述缩减运算过程中采用饱和操作以防止所述8比特整数溢出。

在第一矩阵的一维化过程中，对数据内容非零的n阶方阵进行了行数和列数的记录，根据一个n阶方阵记录保存的行数列数，就可以知晓该n阶方阵在第一矩阵中的具体位置。在第一矩阵中，总行数是n的整数倍，总列数也是n的整数倍。例如，低密度奇偶校验码矩阵包含16200列、5400行数据，n为360，那么在转换得到的第一矩阵中就包括45列、15行n阶方阵。其中，n阶方阵的列数为1至15其中任意一个，行数为1至45其中任意一个。根据n阶方阵的具体列数和行数就可以确定该n阶方阵在第一矩阵中的具体位置。

在通过行数、列数确定了n阶方阵在第一矩阵中的位置后，就可以根据一维化过程中记录保存的n阶方阵的数据内容确定第一矩阵的数据内容。

在对第一矩阵中的数据内容非零的n阶方阵进行记录保存之后，就可以根据数据内容非零的n阶方阵还原出第一矩阵的编码。具体的，可以根据保存的数据内容非零的n阶方阵的行数和列数确定该n阶方阵在第一矩阵中的具体位置，并根据保存的该n阶方阵的数据内容确定该具体位置的数据内容。

在本申请实施例中，可以同时对多个数据内容非零的所述n阶方阵进行处理，由于数据内容非零的所述n阶方阵都是相互独立的，同时进行解码时不会发生相互干扰的情况。例如，如果第一矩阵中每一行包括m个n阶方阵，即可从所有的数据内容非零的n阶方阵中，将行数相同的n阶方阵同时提取出来，即同时提取m个n阶方阵，再根据n阶方阵的行数分别确定各个n阶方阵的具体位置，并再根据n阶方阵的数据内容确定该位置的具体数据内容。基于低密度奇偶校验码矩阵的特性，变换得到的第一矩阵中每一行中数据内容非零的n阶方阵的数量是相同的。在进行完所有数据内容非零的n阶方阵的处理，第一矩阵中其他位置的n阶方阵包含的各个元素就都是零，从而完成整个低密度奇偶校验码矩阵的解码。

在实际处理中，利用GPU可以并行处理数据的特点，采用相同的指令同时并行的处理数据内容非零的n阶方阵。相比现有技术中串行进行解码，处理速度更快，解码效率更高。

在本申请实施例中，在对低密度奇偶校验码矩阵进行解码的过程中，通过对低密度奇偶校验码矩阵进行转换，使得转换后的矩阵包含多个n阶方阵，在解码过程中，仅针对数据内容非零的n阶方阵进行处理，由于低密度奇偶校验码矩阵为稀疏矩阵，数据内容非零的n阶方阵的数量要远远小于零元素的数量，使得解码过程的运算量降低，解码效率得到提高。并且，利用GPU并行处理数据的特点，可同时分多个线程对数据内容非零的n阶方阵进行处理，提高了低密度奇偶校验码矩阵的解码速度，提升了GPU的利用率。

左子矩阵和右子矩阵都为稀疏矩阵，使得转换后的第一矩阵也为稀疏矩阵。在现有技术中，由于低密度奇偶校验码矩阵为稀疏矩阵，其中包含有大量的零元素，在进行解码过程中，仍然需要对这些零元素进行保存、判断的操作，就会重复的多次的进行数据的读取、判断，而这些零元素实质上是没有编码意义的，针对零元素的读取和判断就会大量占用解码时间和硬件资源。

在本申请实施例中，在数据结构上，可以利用高码率规格下左子矩阵中的单位子矩阵缩减稀疏矩阵规模；在数据表示上，可以采用数据定点化方案；在指令上，使用constant存储器保存校验矩阵，以及在对全局变量访问时使用软件流水线提升存储器效率等；在平台上，可以设置帧级并行度，增加并发线程数；在算法上，可以采用折中分层译码处理方式。本申请通过多层次多种优化手段的组合实现低密度奇偶校验码的快速解码。

本申请还提供了一种数据处理装置200，如图2所示，包括转换模块201、一维化模块202和处理模块203。具体实现方法与上述方法实施例相同，这里不再赘述。

综上所述，利用本发明提供的数据处理方法，在对低密度奇偶校验码矩阵进行解码过程中，通过行变换将低密度奇偶校验码矩阵转换为包含多个n阶方阵的形式，并通过矩阵一维化记录保存数据内容非零的n阶方阵的行数、列数和各自的数据内容。从而在解码时，可以同时并行的提取多个数据内容非零的n阶方阵，通过其行数、列数和数据内容确定低密度奇偶校验码矩阵的数据内容，实现解码。解码过程中，无需对矩阵中所有的数据进行处理，只需处理数据内容非零的数据，数据处理量更少，并且一维化后可以实现并行处理，也不会发生干扰和编码信息的损失。解码速度更快，解码效率更高，可以充分利用图形处理器的并行数据处理能力，提高设备的利用率。

在本申请所提供的几个实施例中，应该理解到，所揭露的装置和方法，也可以通过其它的方式实现。以上所描述的装置实施例仅仅是示意性的，例如，附图中的流程图和框图显示了根据本发明的多个实施例的装置、方法和计算机程序产品的可能实现的体系架构、功能和操作。在这点上，流程图或框图中的每个方框可以代表一个模块、程序段或代码的一部分，所述模块、程序段或代码的一部分包含一个或多个用于实现规定的逻辑功能的可执行指令。也应当注意，在有些作为替换的实现方式中，方框中所标注的功能也可以以不同于附图中所标注的顺序发生。例如，两个连续的方框实际上可以基本并行地执行，它们有时也可以按相反的顺序执行，这依所涉及的功能而定。也要注意的是，框图和/或流程图中的每个方框、以及框图和/或流程图中的方框的组合，可以用执行规定的功能或动作的专用的基于硬件的系统来实现，或者可以用专用硬件与计算机指令的组合来实现。

另外，在本发明各个实施例中的各功能模块可以集成在一起形成一个独立的部分，也可以是各个模块单独存在，也可以两个或两个以上模块集成形成一个独立的部分。

所述功能如果以软件功能模块的形式实现并作为独立的产品销售或使用时，可以存储在一个计算机可读取存储介质中。基于这样的理解，本发明的技术方案本质上或者说对现有技术做出贡献的部分或者该技术方案的部分可以以软件产品的形式体现出来，该计算机软件产品存储在一个存储介质中，包括若干指令用以使得一台计算机设备(可以是个人计算机，服务器，或者网络设备等)执行本发明各个实施例所述方法的全部或部分步骤。而前述的存储介质包括：U盘、移动硬盘、只读存储器(ROM，Read-Only Memory)、随机存取存储器(RAM，Random Access Memory)、磁碟或者光盘等各种可以存储程序代码的介质。需要说明的是，在本文中，诸如第一和第二等之类的关系术语仅仅用来将一个实体或者操作与另一个实体或操作区分开来，而不一定要求或者暗示这些实体或操作之间存在任何这种实际的关系或者顺序。而且，术语“包括”、“包含”或者其任何其他变体意在涵盖非排他性的包含，从而使得包括一系列要素的过程、方法、物品或者设备不仅包括那些要素，而且还包括没有明确列出的其他要素，或者是还包括为这种过程、方法、物品或者设备所固有的要素。在没有更多限制的情况下，由语句“包括一个……”限定的要素，并不排除在包括所述要素的过程、方法、物品或者设备中还存在另外的相同要素。

以上所述仅为本发明的优选实施例而已，并不用于限制本发明，对于本领域的技术人员来说，本发明可以有各种更改和变化。凡在本发明的精神和原则之内，所作的任何修改、等同替换、改进等，均应包含在本发明的保护范围之内。应注意到：相似的标号和字母在下面的附图中表示类似项，因此，一旦某一项在一个附图中被定义，则在随后的附图中不需要对其进行进一步定义和解释。

以上所述，仅为本发明的具体实施方式，但本发明的保护范围并不局限于此，任何熟悉本技术领域的技术人员在本发明揭露的技术范围内，可轻易想到变化或替换，都应涵盖在本发明的保护范围之内。因此，本发明的保护范围应所述以权利要求的保护范围为准。