一种基于压缩感知融合前后向匹配追踪的算法的制作方法

本发明涉及一种基于压缩感知融合前后向匹配追踪的算法，属于压缩感知信号处理技术领域。

背景技术：

从降低实际测量系统的采样率和复杂度的角度出发，压缩感知有效地融合了稀疏信号的采样和压缩这两个过程。假定需要获取的最终信号本身是稀疏的或者在经过一定的矩阵变换是稀疏的，那么压缩感知就可以提供一个新的低能耗的采样方案。尤其是当所需要获取信号的稀疏度比较高时，该方案需要的采样率远远低于传统奈奎斯特采样定理。这一低采样率的特性使得压缩感知在无线传感器网络、核磁共振成像等领域有广泛的应用前景。

压缩感知重构算法有很多种，一般来说可以分为三大类，贪婪算法，凸松弛算法和贝叶斯框架。其中，以速度快和操作简单著称的贪婪算法越来越受到人们的关注。而代表性的贪婪算法有匹配追踪(MP)算法和正交匹配追踪(OMP)算法。在它们的基础上，许多学者提出了很多优秀的改进算法，例如：分段正交匹配追踪(StOMP)算法，子空间追踪(SP)算法，压缩采样匹配追踪(CoSaMP)算法，稀疏度自适应匹配追踪(SAMP)算法和前后向匹配追踪(Forward-Backward Pursuit，FBP)算法。与经典的OMP和SP算法相比，FBP算法因其较高的准确重构概率和较低的平均重构误差而有着广泛的应用前景。因此如何进一步提升FBP算法的重构效果成为一个比较棘手的问题。特别是FBP算法的作者经过一系列的实验为FBP算法给出了一套最优的运行参数，使得通过进一步优化参数来提升算法性能的可能性微乎其微。

本发明提出一种融合前后向匹配追踪算法，针对FBP算法已经很难通过优化参数进一步提升重构性能的问题，采用融合的策略，创新性得将工作在相同原理但是仅仅参数不同的算法进行融合，使得本身性能远优于经典算法的FBP算法的重构性能得到了进一步的提升。

技术实现要素：

本发明的目的解决了压缩感知理论中前后向匹配追踪算法重构性能进一步提升的瓶颈问题，提出了一种基于压缩感知理论的融合前后向匹配追踪的算法。

本发明的目的是通过下述技术方案实现的：

(1)输入：感知矩阵Φ，测量值y，前向步长α，后向步长β₁和β₂，支撑集最大限制参数K_max，残差能量终止参数ε，支撑集保留控制参数η；

(2)初始化：初始支撑集初始残差r⁰＝y，初始迭代次数k＝0；

(3)将感知矩阵Φ，测量值y，前向步长α，后向步长β₁以及空集作为输入参数输入到传统的前后向匹配追踪算法中。得到输出参数：信号估计值算法迭代退出方式标志flag₁，残差值res₁；

(4)判断算法迭代退出方式标志flag₁是否为1，也就是判断前后向匹配追踪算法是否以残差小于预设阈值的方式退出。如果为1则令信号估计值转到步骤(9)，否则转到步骤(5)；

(5)令T₁为估计信号中幅度最大的η|T₁′|个元素对应的集合。其中T₁′为估计信号的估计支撑集，|T₁′|为集合T₁′的势；

(6)将感知矩阵Φ，测量值y，前向步长α，后向步长β₂以及集合T₁作为输入参数输入到传统的前后向匹配追踪算法中。得到输出参数：信号估计值算法迭代退出方式标志flag₂，残差值res₂；

(7)判断算法迭代退出方式标志flag₂是否为1，也就是判断前后向匹配追踪算法是否以残差小于预设阈值的方式退出。如果为1则令信号估计值转到步骤(9)，否则转到步骤(8)；

(8)比较残差res₁和res₂，找到其中的较小者，选择相应的信号估计值作为最终的信号估计值

(9)输出稀疏信号估计值

本发明在提高算法性能的过程中，对于迭代失败的算法，并不是完全舍弃后，继续优化运行参数重新运行算法。而是采用融合策略，充分挖掘失败算法中的有用信息，并以此作为融合到另一算法中的基础。

本发明在对算法进行融合时，融合的另一方仅仅是不同参数设置的同种算法，它不需要其他额外的先验信息，也不需要其他算法作为辅助。

【本发明的优点和积极效果】

与现有技术相比，本发明具有如下优点和积极效果：

第一，在前后向匹配追踪算法迭代失败后，并不是完全舍弃，而是利用融合策略，充分发掘失败算法中的有用信息，为提升算法性能提供融合的基础。

第二，在算法融合过程中，融合的另一方仅仅是不同参数设置的同种算法，它不需要其他额外的先验信息，也不需要其他算法作为辅助。

【附图说明】

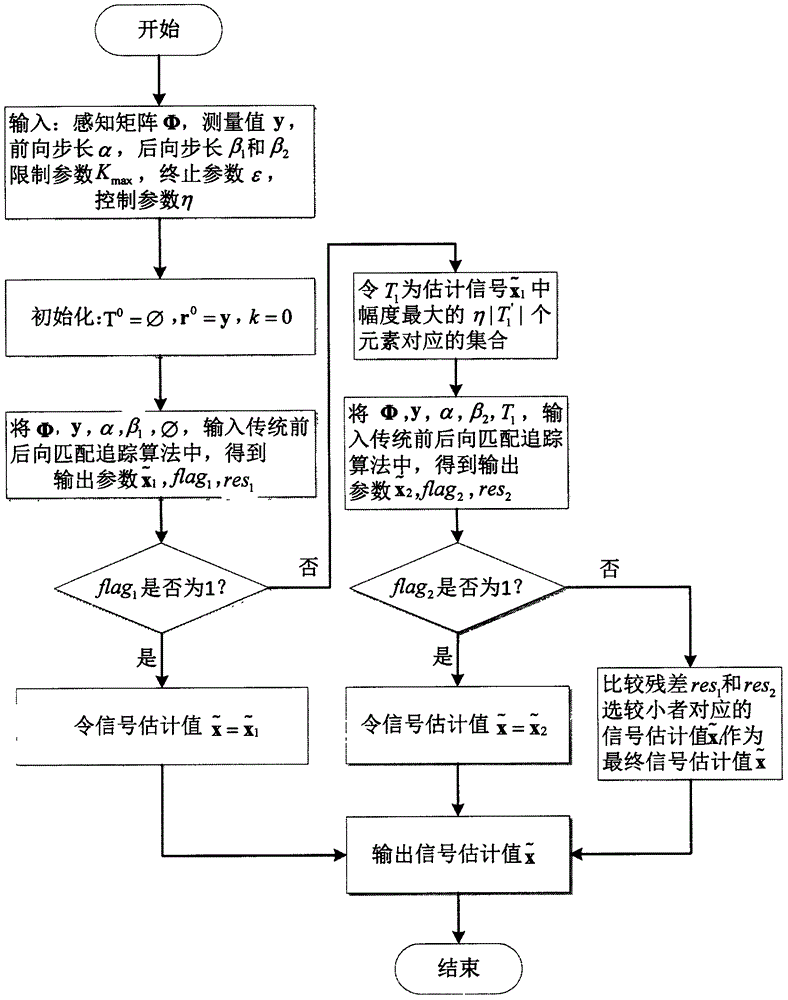
图1是本发明提出的一种基于压缩感知融合前后向匹配追踪的算法流程图；

图2是本发明与OMP、SP、FBP算法的对高斯稀疏信号在准确重构概率上的比较图；

图3是本发明与OMP、SP、FBP算法的对高斯稀疏信号在平均重构误差上的比较图。

【具体实施方式】

为使本发明的实施方案与意义优势表述得更为清楚，下面结合附图及重构效果比较图，对本发明进行更为详细的说明。

图1是本发明提出的一种基于压缩感知融合前后向匹配追踪的算法流程图，算法具体流程如下：

(1)输入：感知矩阵Φ，测量值y，前向步长α，后向步长β₁和β₂，支撑集最大限制参数K_max，残差能量终止参数ε，支撑集保留控制参数η；

(2)初始化：初始支撑集初始残差r⁰＝y，初始迭代次数k＝0；

(3)将感知矩阵Φ，测量值y，前向步长α，后向步长β₁以及空集作为输入参数输入到传统的前后向匹配追踪算法中。得到输出参数：信号估计值算法迭代退出方式标志flag₁，残差值res₁；

(4)判断算法迭代退出方式标志flag₁是否为1，也就是判断前后向匹配追踪算法是否以残差小于预设阈值的方式退出。如果为1则令信号估计值转到步骤(9)，否则转到步骤(5)；

(5)令T₁为估计信号中幅度最大的η|T₁′|个元素对应的集合。其中T₁′为估计信号的估计支撑集，|T₁′|为集合T₁′的势；

(6)将感知矩阵Φ，测量值y，前向步长α，后向步长β₂以及集合T₁作为输入参数输入到传统的前后向匹配追踪算法中。得到输出参数：信号估计值算法迭代退出方式标志flag₂，残差值res₂；

(7)判断算法迭代退出方式标志flag₂是否为1，也就是判断前后向匹配追踪算法是否以残差小于预设阈值的方式退出。如果为1则令信号估计值转到步骤(9)，否则转到步骤(8)；

(8)比较残差res₁和res₂，找到其中的较小者，选择相应的信号估计值作为最终的信号估计值

(9)输出稀疏信号估计值

其中传统的前后向匹配追踪算法的流程也在这里给出：

(1)输入：感知矩阵Φ，测量值y，前向步长α，后向步长β，支撑集最大限制参数K_max，残差能量终止参数ε，初始支撑集T⁰；

(2)初始化：初始残差r⁰＝y，初始迭代次数k＝0，算法迭代退出方式标志flag＝1；

(3)迭代次数k＝k+1；

(4)将残差r^k-1与感知矩阵Φ的每一列做内积，选出其中内积最大的α个原子存入集合T_f中，即将集合T_f与上次迭代估计支撑集T^k-1进行合并得到即并用最小二乘法计算出对应的逼近值w，即

(5)令集合T_b为w中幅值最小的β个元素对应的原子组成的集合，即将T_b从集合中删去，得到第k次迭代的估计支撑集

(6)用最小二乘法计算出T^k对应的逼近值w，并由此计算出新的残差

(7)如果估计支撑集T^k中元素个数大于K_max则令flag＝0，转到(9)，否则转到(8)

(8)如果残差能量||r^k||₂≥ε||y||₂则转到(3)，否则转到(9)；

(9)先将信号估计值清零然后将估计值中对应估计支撑集T^k的元素进行赋值令残差res＝||r^k||₂；

(10)输出信号估计值算法迭代退出方式标志flag和残差res。

图2和图3分别是本发明与OMP，SP和FBP算法对高斯稀疏信号在准确重构概率和平均重构误差上的比较图。其中FBP1的参数为α＝20，β＝19，该参数为FBP作者推荐的最优参数。FBP2的参数为α＝20，β＝18。本发明算法的参数为α＝20，β₁＝19，β₂＝18，η＝0.2。其中FBP1和FBP2是本发明算法所融合的两个不同参数的FBP算法。测量矩阵Φ为128×256的独立同分布高斯随机矩阵。原始信号x是长度为256的一维高斯稀疏信号，稀疏度为K。K的变化范围为15到45.支撑集最大限制参数K_max＝50。残差能量终止参数ε＝10^-6。对每个稀疏度K，实验均重复500次。在实验中，准确重构概率表示准确恢复的测试信号和整个测试数据的比率。其中，准确恢复条件为平均重构误差用平均归一化最小均方误差(Average Normalized Mean-Squared-Error，ANMSE)进行衡量，定义为其中表示第i个测量向量x_i的重构向量。

从图2可以看出，FBP1，FBP2和本发明算法的准确重构概率均远高于OMP和SP这些经典的压缩感知重构算法。而本发明算法的性能更优于所融合的FBP1和FBP2算法。而其中FBP1是FBP算法推荐的最优参数。

图3中，本发明依然是最优算法，其平均重构误差是所有对比算法中最低的。通过数值仿真实验证明本发明相比前后向匹配追踪算法对稀疏信号的重构更有优势。