一种基于结构化测量矩阵的块稀疏信号恢复方法与流程

本发明属于块稀疏信号恢复方向一种基于结构化测量矩阵的块稀疏信号恢复方法。该发明是为了降低块稀疏信号恢复的复杂度。稀疏信号测量和恢复是压缩感知领域的主要工作。

背景技术：

自从2006年有关压缩感知技术的奠基性文章发表以来，压缩感知技术得到了广泛的关注。在诸如图像视频信号处理、通信信号处理等各个领域，压缩感知技术都成了有力的研究和运用工具。压缩感知技术称，当信号具有稀疏性(即待恢复信号向量中有很多零元素，或者很多非零信号非常小以至于可以忽略)或者在某个域上具有稀疏性，则测量这些信号可以用低于奈奎斯特的采样频率。当采用一定的恢复方法，可以从欠定的采样系统中重构稀疏信号。这是一个根本性的突破。最初的压缩感知技术研究还针对一般性的稀疏信号，即信号向量中的非零元素是随机分布于向量中的。随着研究的进行以及领域的多样化，具有块结构的稀疏信号得到关注。块稀疏信号广泛存在于在实际应用中，如多波段信号、稀疏信道增益向量、雷达脉冲信号、图像信号等。块稀疏信号是指，将信号向量分成块，则只有某些块的信号是非零的。已有研究表明，将待恢复稀疏信号的块结构考虑进去，稀疏恢复可以获得更好的准确性。

压缩感知技术有三个要点：1、稀疏信号；2、稀疏恢复；3、测量矩阵。

其中，稀疏恢复时，由于非零信号的位置预先并不知道，算法需要对所有信号进行估计。以正交匹配追踪(orthogonal matching pursuit，OMP)迭代恢复算法为例，OMP需要在每一迭代步骤通过相关计算和比较选择出最有可能的非零元素位置，然后再进行信号更新，直至迭代结束。因此，可以说，测量矩阵的维度(同时也是稀疏信号向量的长度)直接影响稀疏恢复的准确性。

其次，测量矩阵至关重要，因为它直接决定了稀疏信号测量的有效性，同时也决定了稀疏信号的恢复性能，包括准确性和复杂度。针对测量矩阵的设计，已有相当多得研究工作。已有的结论表明，当测量矩阵满足约束等距特性(restricted isometryproperty，RIP)时，稀疏信号可以以很高概率得到准确恢复。幸运的是，RIP条件很容易得到满足，比如随机的高斯矩阵、伯努利矩阵都可以作为测量矩阵。关于块稀疏恢复的测量矩阵设计也有一些研究。不过，这些设计工作均以提高稀疏恢复的准确性为出发点，它们设计出密集的测量矩阵，以降低稀疏恢复复杂度为目的的测量矩阵设计工作凤毛麟角。

当块稀疏信号的块长为1时，即信号的非零元素随机分布于向量中，因此随机稀疏是块稀疏的一个特例。鉴于此，为了便于表述，统一将稀疏信号恢复称为块稀疏信号恢复。

技术实现要素：

本发明为克服现有技术中存在的不足之处，提出一种基于结构化测量矩阵的块稀疏信号恢复方法，以期能降低块稀疏恢复的复杂度问题，使得在待恢复的信号块数量非常多且非常稀疏的情况下依然能接受相应复杂度并完成恢复。

本发明为达到上述发明目的，采用如下技术方案：

本发明一种基于结构化测量矩阵的块稀疏信号恢复方法的特点是按如下步骤进行：

步骤1、信号恢复端产生一个行数为T、列数为N×M＝NM的用于测量N个维度为M×1的块稀疏信号h的测量矩阵B＝[B₁,B₂,…,B_n,…,B_N]，即：

其中，表示所述测量矩阵B的第n个维度为T×M的子矩1≤n≤N，1≤t≤T；所述测量矩阵B中的元素服从高斯或者伯努利分布；

步骤2、将所述测量矩阵B的N个子矩阵按顺序分为Q个单元，其中，前Q-1个单元所包含的子矩阵数量为第Q个单元包含的子矩阵数量为即：

其中，表示第q个单元，1≤q≤Q；

步骤3、保留所述测量矩阵B的第(q-1)×L+1行至第q×L行属于第q个单元的列向量部分，所述第(q-1)×L+1行至第q×L行不属于第q个单元的列向量部分全部置为“0”，1≤q≤Q；且参数L的选择满足Q×L≤T；由此产生结构化的测量矩阵D，即；

其中，

步骤4、所述信号恢复端利用式(1)对所述块稀疏信号进行线性测量，得到测量向量

式(1)中，h_n为所述块稀疏信号h的第n个维度为M×1的信号块，z是维度为T×1的噪声向量；y_q为所述测量向量y的第(q-1)×L+1个测量值到第q×L个测量值构成的L×1维向量，为所述测量向量y的第q×L个测量值到第T个测量值构成的(T-Q×L+1)×1维向量；

步骤5、根据所述测量向量y对所述块稀疏信号h进行恢复：

步骤5.1、设定能量检测门限其中，λ²是所述测量矩阵D前Q×L行非零元素的平均能量，是所述块稀疏信号h中非零元素的平均功率，是所述噪声向量z中元素的平均功率，p是所述能量检测可接受的漏检概率，F^(-1)(p)是函数的反函数；漏检是指将包含所述非零信号块的单元检测判决为没有包含所述非零信号块；

步骤5.2、定义变量q；并初始化q＝1，中间变量H＝φ；

步骤5.3、检测判决：

如果则第q个单元被判决为包含所述的非零信号块，将中间变量H和属于第q个单元的测量矩阵部分组合为并赋值给中间变量H；否则，将第q个单元所包含的所述信号块全部恢复为“0”向量；从而使得所述单元能量检测完成部分信号块的恢复；

步骤5.4、将q+1赋值给q，并返回步骤5.3执行，直到q＝Q为止；

步骤5.5、利用稀疏恢复算法对式(2)所示的块稀疏信号h中剩余的信号进行块稀疏估计，从而完成对所述块稀疏信号h的完整估计：

本发明将块稀疏恢复中涉及的测量矩阵设计出具有一定的结构性，并基于测量矩阵的结构提出了相应降低复杂度的块稀疏恢复算法。与已有技术相比，本发明的有益技术效果体现在：

1、基于本发明设计的结构化测量矩阵的单元能量检测可以在进行细致的块稀疏信号恢复之前确认一部分单元所包含的信号块全为零，这些信号块便已经完成恢复了。由此，当进行更为细致的块信号恢复时，需要恢复的信号块数量就降低了。单元能量检测和判决的复杂度非常低，因此发明降低了块稀疏信号恢复的复杂度；

2、当原本需要恢复的块信号数量非常大且信号很稀疏时，基于本发明设计的结构化的测量矩阵的稀疏信号恢复方法可以通过能量检测首先恢复非常多零信号向量，此时便可极大降低了信号恢复的复杂度；

3、某些条件下，基于本发明设计的结构化的测量矩阵的稀疏信号恢复方法还可以获得更准确的信号恢复。如此便在提高信号恢复的准确性和降低恢复复杂度方面均取得增益。

附图说明

图1a为采用本发明在块稀疏信号恢复准确性能上的一个仿真图；

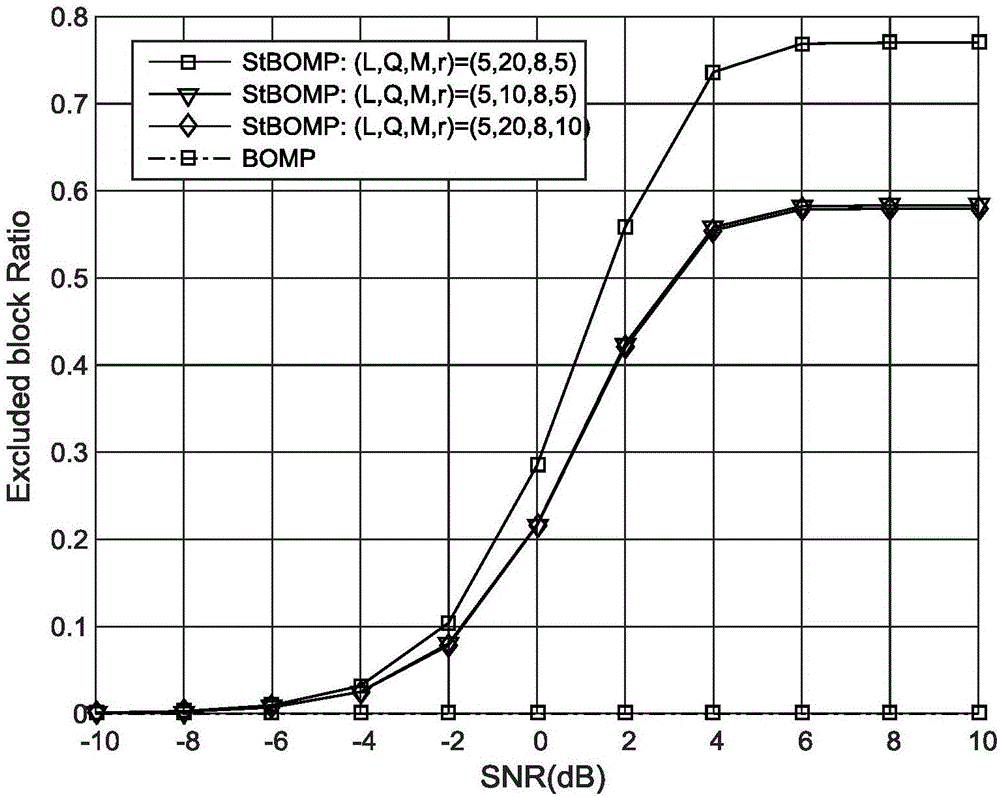
图1b为表明本发明在降低块稀疏信号恢复复杂度性能上的一个仿真图。

具体实施方式

本实施例中，块稀疏信号广泛存在于在实际应用中，如多波段信号、稀疏信道增益向量、雷达脉冲信号、图像信号等。本实施例中考虑的块稀疏信号恢复包括如下过程：测量矩阵设计，块稀疏信号的测量，块稀疏信号的恢复。假设测量矩阵的行数为T，列数为N×M＝NM，用于测量N个维度为M×1的块稀疏信号。块稀疏信号指的是，N个信号块中有很多信号块元素全为0。具体地，一种基于结构化测量矩阵设计的块稀疏信号恢复是按如下步骤进行的：

步骤1、信号恢复端(同时也是信号测量端)产生一个行数为T、列数为NM的用于测量N个维度为M×1的块稀疏信号h的测量矩阵B＝[B₁,B₂,…,B_n,…,B_N]，即：其中，表示所述测量矩阵B的第n个维度为T×M的子矩1≤n≤N，1≤t≤T；测量矩阵B中的元素可以服从高斯或者伯努利等分布；

步骤2、将测量矩阵B的N个子矩阵按顺序分为Q个单元，其中，前Q-1个单元所包含的子矩阵数量为第Q个单元包含子矩阵数量为如此地，测量矩阵可以写成如下形式：

其中，表示第q个单元，1≤q≤Q；

步骤3、保留测量矩阵D的第(q-1)×L+1行至第q×L行属于单元的列向量部分，所述第(q-1)×L+1行至第q×L行不属于单元的列向量部分全部置为“0”，1≤q≤Q；参数L的选择需要满足Q×L≤T；由此产生结构化的测量矩阵D，即：

其中，

步骤4、信号恢复端利用式(1)对块稀疏信号采用上面设计的测量矩阵D进行线性测量，得到测量向量

y＝Dh+z (1)

式(1)中，h_n为块稀疏信号h的第n个维度为M×1的信号块，1≤n≤N；z是维度为T×1的噪声向量；y_q为测量向量y的第(q-1)×L+1个测量值到第q×L个测量值构成的L×1维向量，为测量向量y的第q×L个测量值到第T个测量值构成的(T-Q×L+1)×1维向量；

步骤5、根据测量向量y对块稀疏信号h进行恢复，首先对Q个单元进行能量检测以判决每一个单元是否包含非零信号块，其次对包含非零信号块的单元进行恢复，如下：

步骤5.1、设定能量检测门限其中，λ²是测量矩阵D前Q×L行非零元素的平均能量，是块稀疏信号h中非零元素的平均功率，是噪声向量z中元素的平均功率，p是能量检测可接受的漏检概率，F^(-1)(p)是函数的反函数；漏检是指将包含非零信号块的单元检测判决为没有包含非零信号块；此处门限的设定基于这样一个近似：假设单元q包含一个非零信号块，将测量向量y_q的每一个元素近似为均值为0方差为的高斯变量。

步骤5.2、定义变量q；并初始化q＝1，中间变量H＝φ；

步骤5.3、检测判决：

如果则第q个单元被判决为包含非零信号块，将中间变量H和属于第q个单元的测量矩阵部分组合为并赋值给中间变量H；否则，将第q个单元所包含的信号块全部恢复为“0”向量；如此地，单元能量检测便完成了部分信号块的恢复；

步骤5.4、将q+1赋值给q，并返回步骤5.3执行，直到q＝Q为止；

步骤5.5、利用已有的稀疏恢复算法对式(2)所示的块稀疏信号h中剩余的信号进行块稀疏估计，从而完成对块稀疏信号h的完整估计：

上述尚未被步骤5.2—5.4恢复的剩余的信道增益向量仍然可能是稀疏的，因此需要借助压缩感知领域的稀疏信号恢复算法来恢复比如在M＞1的场景，对的稀疏恢复可以采用块正交匹配追踪(BOMP，block orthogonal matching pursuit)算法。同时，有必要指出，基于所设计的结构化测量矩阵，步骤5.2—5.4是为实现块稀疏信号恢复复杂度降低的关键步骤，通过能量检测，本发明以很小的计算代价排除了一些元素全为“0”的稀疏信号块；在某些条件下，排除的信号块的数量可以很大，从而极大降低块稀疏信号恢复的复杂度。

由上述发明的基于结构化测量矩阵的块稀疏信号恢复方法的效果可以由仿真图1a和图1b表现出来。图1a的仿真结果中，纵坐标为归一化的均方误差(normalizedMSE，normalizedmean square error)，横坐标为信噪比SNR(定义为1/σ²，单位为dB)；曲线标注中BOMP为基于密集的测量矩阵的块稀疏信号恢复仿真结果，StBOMP表示为采用本发明所设计的结构化测量矩阵的块稀疏信号恢复仿真结果；仿真中结构化的测量矩阵的非零元素取自均值为0方差为1的复高斯分布，对应地，作为参照的密集矩阵的元素是均值为0方差为(T-Q×L+L)/T的复高斯变量以保障测量矩阵的列能量统计上都一样。标注给出的参数(L,Q,M,r)中，r表示非零信号块的数量，其它参数为T＝200，N＝80，p＝0.0001，BOMP的迭代次数设置为r。待恢复的非零信号块的元素产生成均值为0方差为1的高斯变量。图1a的仿真结果表明，基于结构化的测量矩阵在某些参数下可以取得更低的归一化的均方误差。大体上，只要T-Q×L+L不会太小，测量矩阵带来的归一化的均方误差与密集的测量矩阵相差很小。图1b的仿真中，纵坐标为步骤5.5开始之前已经由单元检测恢复为“0”的信号块数量占总信号块数量的比例，仿真结果体现了本发明的目标。随着SNR的增加，可以预先恢复的信号块数量越来越多。给定参数下，当这一比例大于等于0.6875时，所设计的测量矩阵和单元检测可以将原本欠定的信号恢复问题转化为超定的信号恢复问题，这样可以避免迭代过程而直接用最小二乘方法恢复剩余信号，这就极大降低了信号恢复的复杂度。另一方面，各个参数的设置对发明的效果有一定的影响，基本地，需要保证T≥QL；其次，Q＞r能比较好地保证复杂度的降低。本发明可以适用于M＝1和M＞1的情况，当σ²→0时，L＝1即可。