一种用于调制宽带转换器的非理想滤波器的补偿方法与流程

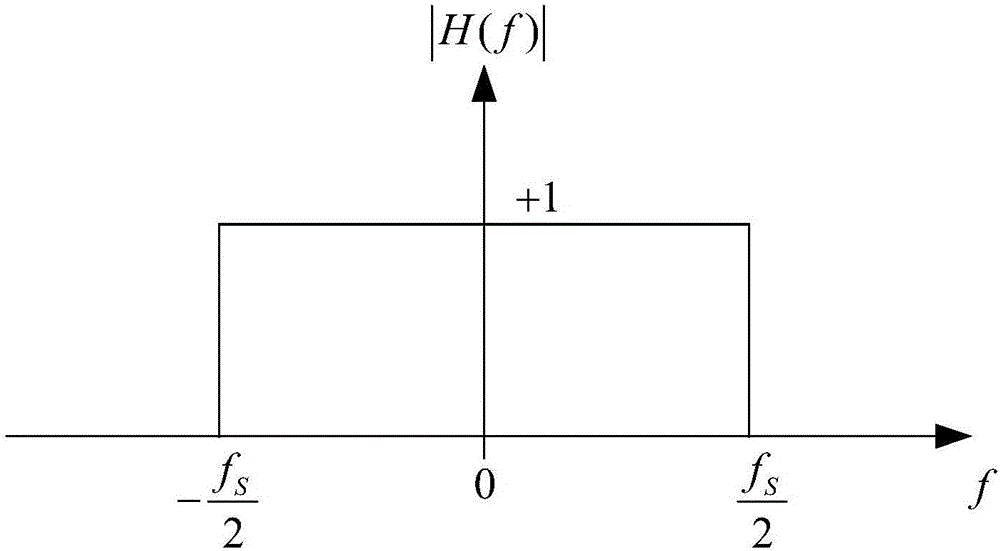
本发明涉及信号处理领域，具体涉及一种针对调制宽带转换器硬件系统的滤波器的补偿方法。

背景技术：

2004年由E.Candès、T.Tao等人提出的压缩感知(Compressed Sensing,CS)或称称压缩采样(Compressive Sampling，CS)是一种全新的信号采集理论，它充分利用信号稀疏性或可压缩性，对信号先进行压缩再采样，打破了传统信号采集中先采样后压缩传输的观念。CS理论指出，当信号具有稀疏性时，可以通过全局观测的方式同时实现信号压缩和采样，只需要采集少量非自适应的线性观测值就可以获得信号的全部信息，所以采样率远低于奈奎斯特采样率。

由CS理论发展出的多种压缩采样结构，如随机解调系统、随机调制预积分系统、调制宽带转换器(Modulated Wideband Converter，MWC)等。其中调制宽带转换器系统具有硬件实现可行性更好的特点，可以实现对频域稀疏的多频带信号的压缩采样与重构，仅用商业器件解决了高频信号的采样硬件设备庞大昂贵问题。调制宽带转换器的结构如图1所示，由多组结构相同的通道组成，每个通道主要由乘法器、低通滤波器、低速采样模块组成。

多频带信号进入系统后，同时与多路不同的伪随机序列进行混频，这个过程利用了通信理论中的频谱扩展技术，混频前端将信号频谱搬移到基带内进行处理，混频后的信号经过一个理想低通滤波之后被低速ADC进行均匀采样，理想低通滤波器的频响特性如图2所示，多路采样数据经过重构后便可以得到原始信号的奈奎斯特采样数据。

在调制宽带转换器的理论论述过程中，需要使用理想低通滤波器对调制后的模拟信号进行处理。而在实际应用中，理想低通滤波器很难通过现有硬件设备条件实现，人们往往使用高阶巴特沃斯或切比雪夫滤波器进行代替。

实际的低通滤波器与理想低通滤波器相比，主要存在以下三点不足：

1)频响函数H(f)在通带不一定是平坦的，即有可能存在通带波动与衰减；

2)H(f)不具备矩形频响特性，即通带与阻带之间无法实现骤变；

3)阻带的|H(f)|不是严格的0，即阻带衰减不够。

由于实际的低通滤波器存在以上的不足，所以此时对调制宽带转换器系统采样进行频域分析时，便不可忽略滤波器频响函数H(f)带来的影响，如果不消除这些影响系统便难以实现信号的理想重构。

技术实现要素：

本发明为了解决实际的低通滤波器与理想低通滤波器之间的非理想差异使得信号的理想重构难以实现，从而提出一种用于调制宽带转换器的非理想滤波器的补偿方法。

一种用于调制宽带转换器的非理想滤波器的补偿方法，包括以下步骤：

步骤一、假设每次采样时长为t，结合理想滤波器采样频率f_s得到理想滤波器情况下每个通道的采样点数N₁；

步骤二、使用非理想滤波器时，非理想滤波器采样频率f_s′满足|H(f_s′/2)|≤-60dB，且非理想滤波器的截止频率满足f_p≥f_s；根据非理想滤波器采样频率f_s′和采样时长为t得到实际情况下每个通道的采样点数N₂；其中H(·)表示频响特性；

步骤三、获得非理想滤波器在支持集f₁的频点处的频响特性

f₁＝n₁f_s/N₁

n₁∈[-N₁/2,N₁/2]且n₁∈Z

中，j为虚数单位，f为支持集f₁中的频点，T_s′为非理想滤波器采样时间间隔；Z为整数集合；

步骤四、确定物理硬件系统采样数据需要补偿的频点位置：采样数据补偿频点的支持集f₂满足且满足f₂在[-f_s/2,f_s/2]范围内的支持集等于f₁；

f₂＝n₂f_s'/N₂

n₂∈[-N₂/2,N₂/2]且n₂∈Z

步骤五、计算补偿频点位置的傅立叶补偿系数

在支持集f₁中相应频点的补偿系数是对应的非理想滤波器频响特性的倒数，对于频点位置的补偿系数为0，如下：

步骤六、在物理硬件系统中进行非理想滤波器的傅立叶系数补偿：

针对每次在采样时长t内采样得到的数据y_i′[n]，首先进行N₂点的离散傅立叶变换得到由步骤五得到的傅立叶补偿系数在相应频点进行对应相乘，得到补偿后的采样数据的傅立叶变换

步骤七、对进行逆离散傅里叶变换得到补偿后的数据y_i″[n]。此时的采样数据和理论上理想滤波器的差异很小，唯一的区别是采样率f_s′≥f_s。y_i″[n]可直接进入后续的信号重构过程，重构信号的误差和使用理想滤波器情况下的差异很小。

优选地，步骤一所述的N₁＝f_s*t。

优选地，步骤二所述的N₂＝f_s′*t。

优选地，步骤二所述的非理想滤波器采样频率f_s′＝1/T_s′。

优选地，步骤三中通过仪器测量或者随机序列冲击响应法获得非理想滤波器在支持集f₁的频点处的频响特性

本发明具有以下有益效果：

本发明充分利用了信号在模拟域和离散域的特性，通过对调制宽带转换器采样得到的数据直接在频域进行傅立叶系数补偿，解决了调制宽带转换器在硬件实现过程中非理想滤波器因素对信号重构的影响，实现了信号的理想重构。通过理论分析及实验结果得到，本发明方法操作简单，使用方便，能够补偿大多数类型滤波器的非理想特性，重构出来的信号误差非常小。

附图说明

图1为调制宽带转换器的结构示意图；

图2为理想低通滤波器的频响特性曲线；

图3为应用本发明后的调制宽带转换器系统结构示意图；

如图4-图6为对比实验效果图；其中，图4为原始被测信号，图5是未进行非理想滤波器补偿的信号重构结果，图6为进行本发明补偿后的信号重构结果；

图7为不同阶数的巴特沃斯、椭圆、切比雪夫I型滤波器经过本发明的补偿后的效果图。

具体实施方式

具体实施方式一：

一种用于调制宽带转换器的非理想滤波器的补偿方法，包括以下步骤：

步骤一、假设每次采样时长为t，结合理想滤波器采样频率f_s得到理想滤波器情况下每个通道的采样点数N₁；

步骤二、使用非理想滤波器时，非理想滤波器采样频率f_s′满足|H(f_s′/2)|≤-60dB，且非理想滤波器的截止频率满足f_p≥f_s；根据非理想滤波器采样频率f_s′和采样时长为t得到实际情况下每个通道的采样点数N₂；其中H(·)表示频响特性；

步骤三、获得非理想滤波器在支持集f₁的频点处的频响特性

f₁＝n₁f_s/N₁

n₁∈[-N₁/2,N₁/2]且n₁∈Z

中，j为虚数单位，f为支持集f₁中的频点，T_s′为非理想滤波器采样时间间隔；Z为整数集合；

步骤四、确定物理硬件系统采样数据需要补偿的频点位置：采样数据补偿频点的支持集f₂满足且满足f₂在[-f_s/2,f_s/2]范围内的支持集等于f₁；

f₂＝n₂f_s'/N₂

n₂∈[-N₂/2,N₂/2]且n₂∈Z

步骤五、计算补偿频点位置的傅立叶补偿系数

在支持集f₁中相应频点的补偿系数是对应的非理想滤波器频响特性的倒数，对于频点位置的补偿系数为0，如下：

步骤六、在物理硬件系统中进行非理想滤波器的傅立叶系数补偿：

针对每次在采样时长t内采样得到的数据y_i′[n]，首先进行N₂点的离散傅立叶变换得到由步骤五得到的傅立叶补偿系数在相应频点进行对应相乘，得到补偿后的采样数据的傅立叶变换

步骤七、对进行逆离散傅里叶变换得到补偿后的数据y_i″[n]。此时的采样数据和理论上理想滤波器的差异很小，唯一的区别是采样率f_s′≥f_s。y_i″[n]可直接进入后续的信号重构过程，重构信号的误差和使用理想滤波器情况下的差异很小。

虽然在物理上无法实现理想滤波器，但是按照本发明直接对采样值进行处理，使其在滤波和补偿后类似于通过了一个理想滤波器，结构如图3所示，图中，x(t)为被测的多频带信号，p_i(t)为周期伪随机函数，h(t)表示低通滤波器，表示傅立叶补偿系数；DFT为离散傅里叶变换(Discrete Fourier Transform)，IDFT为离散傅里叶逆变换(Inverse Discrete Fourier Transform)。

具体实施方式二：

本实施方式步骤一所述的N₁＝f_s*t。

其他步骤和参数与具体实施方式一相同。

具体实施方式三：

本实施方式步骤二所述的N₂＝f_s′*t。

其他步骤和参数与具体实施方式一或二相同。

具体实施方式四：

本实施方式步骤二所述的非理想滤波器采样频率f_s′＝1/T_s′。

其他步骤和参数与具体实施方式一至三之一相同。

具体实施方式五：

本实施方式步骤三中通过仪器测量或者随机序列冲击响应法获得非理想滤波器在支持集f₁的频点处的频响特性

其他步骤和参数与具体实施方式一至四之一相同。

实施例

为了验证本发明方法的优异补偿效果，将进行两个验证实验。

实验1中将对比证明本发明的有效性，实验中使用一个5阶椭圆滤波器，如图4-图6所示，图4为原始被测信号，图5是未进行非理想滤波器补偿的信号重构结果，图6为进行本发明补偿后的信号重构结果。实验1可以看出在使用了本发明的补偿方法后的信号重构结果与原始被测信号一致，而未进行补偿的重构信号则发生很大的畸变，证明了本发明的有效性。

实验2则对不同阶数的巴特沃斯、椭圆、切比雪夫I型滤波器进行本发明的补偿实验，如图7所示，由实验结果可以发现这三种滤波器的阶数在4阶或以上时，经过本发明重构后信号的信噪比(与原始被测信号的差异程度)可达30dB以上，补偿效果非常好，证明了本发明的广泛适用性。