一种基于LFBT的多分量SFM信号参数估计方法与流程

本发明涉及信号与信息处理技术，具体涉及一种多分量正弦调频信号的参数估计方法。

背景技术：

非平稳信号广泛存在于自然界之中。根据非平稳信号的时间统计特性是否呈线性分为线性调频信号和非线性调频信号。正弦调频(Sinusoidal Frequency Modulated,SFM)信号是一类在实际中最为常见的非线性调频信号，广泛应用于雷达目标特征提取、生物医学疾病诊断和地震勘测中，且通常以多分量形式存在。在雷达目标特征提取中，SFM信号包含了雷达微动目标的精细运动信息与结构信息，是目标识别的重要依据之一；在生物医学疾病诊断中，脑电波信号以及核磁共振信号都为SFM信号，信号的不同参数反映了检查者的身体状况。因此，SFM信号的参数提取具有重要的研究意义。

SFM信号的参数估计通常采用将信号变换到不同域上进行。为解决多分量SFM信号的参数估计问题，孙志国等在《基于离散正弦调频变换的多分量正弦调频信号参数估计方法》(系统工程与电子技术,2012,34(10):1973-1979)中，通过SFM信号在离散正弦调频变换(Discrete Sinusoidal Frequency-Modulated Transform,DSFMT)域的聚敛特征，完成多分量SFM信号的频率估计。彭勃等在《A Sinusoidal Frequency Modulation Fourier Transform for Radar-Based Vehicle Vibration Estimation》(IEEE Transactions on Instrumentation and Measurement,2014,63(9):2188-2199)中，通过在正交三角基函数上进行信号投影，采用正弦调频傅立叶变换(Sinusoidal Frequency Modulation Fourier Transform,SFMFT)进行SFM信号的频率估计。然而，该频谱中除各子目标微动频率的谱线外，同时存在若干干扰项谱线，影响了参数提取的准确性。

针对多分量SFM信号的参数估计问题，通过分析贝塞尔函数的相关性质，在FBT的基础上提出对数傅立叶-贝塞尔变换(Logarithmic Fourier-Bessel Transform,LFBT)，LFBT将信号的相位项投影在贝塞尔函数上，贝塞尔函数的幅值衰减特性使得它能够很好地被用于表示非平稳信号，进而提出一种基于LFBT的多分量SFM信号参数估计方法，准确地进行各分量SFM信号调制频率的参数估计。

技术实现要素：

本发明的目的在于克服上述现有技术中的不足之处，提出一种基于LFBT的多分量SFM信号参数估计方法，包括下列步骤：

第一步：判断多分量SFM信号是否存在相位模糊，若存在则进行相位解模糊处理；

若离散采样信号总相位偏移过大，则会产生相位模糊；由于信号的相位测量值位于区间(-π,π)上，因此当总相位偏移超过2π时产生相位模糊现象；总相位偏移达到2π的整数K倍时，K为相位模糊数；相位模糊可以通过相邻采样点之间的相位差值进行修正，当相邻采样点之间的相位差值不超过π时，可通过如下方法进行修正

其中pha(n)＝Im[ln s(n)]，phar(n)为修正后的相移和测量值之差；因此，当信号相邻采样点的相位差值不超过π时，可进行相位解模糊处理。

第二步：选择合适的LFB级数分辨率k，对解模糊后的多分量SFM信号进行LFBT；

已知正弦调频信号模型为

s(t)＝R exp{j[a sin(ωt)+b cos(ωt)]} (2)

其中R为信号幅度，a、b分别为SFM信号的调制指数，ω为调制频率；

定义信号s(t)的LFBT为

其中J_α(t)为第一类α阶贝塞尔函数，ω为变换域变量；对应的对数傅立叶-贝塞尔逆变换(Inverse Logarithmic Fourier-Bessel Transform,ILFBT)为

在有限区间上傅立叶变换(Fourier Transform,FT)表现为傅立叶级数，与傅立叶变换相似，LFBT在有限区间上以LFB级数(LFB Series)表示；在实际信号处理中，实际信号通常经过离散采样，离散信号的LFB级数表现为信号相位项上的有限项之和

其中n＝1,…,N，N为信号采样点数，t_s为信号采样间隔且N＝T/t_s；第m项LFB系数计算为

其中系数K₁＝2/(N²t_s)为一虚常数，系数随LFB级数项数m变化；由于第α阶贝塞尔函数的正根构成常数列{J_α,m}，因此{K_2,m}也为一不随信号变化的常数列，通常取α＝0；

LFB级数项数与SFM信号的频率调制成分一一对应，第m项LFB级数在频率成分为f_m处取得最大值

因此，对SFM信号进行LFBT变换后，以最大幅值项LFB级数作为SFM信号调制频率的估计；

其中

相邻两项LFB级数对应的频率差值，即频率分辨率计算为

若频率分辨率Δf_m越小，则相邻两项LFB级数对应的理论频率值差值减小，则估计误差也会减小；

将LFB级数分辨率k值引入，当LFB级数分辨率为k时

此时频率分辨率为Δf_m＝1/2πkNt_s，随着LFB级数分辨率k的增大，频率分辨率也会增加；此时估计频率为

其中最大项LFB系数为

此时，相邻两项LFB级数的频率分辨率为

第三步：计算相邻两项LFB级数所在区间的中心误差频率，进行估计频率修正，得到各分量的估计频率；

通过最大项(第项)LFB级数计算出SFM信号的估计频率为通常情况下，频率估计误差f_bias不超过频率分辨率的一半

此时真实频率为相邻第m项与第m+1项LFB系数对应理论频率J_0,m/2πT与J_0,m+1/2πT的平均值；然而这种情况仅适用于一个频率成分仅投影在单根谱线或单个级数上(如FT)；在LFB级数中，一个频率成分投影在若干阶贝塞尔级数上，也就是说，f_m在第m项级数取得峰值同时在邻近的若干阶级数上的投影幅值不为零；

将相邻两项LFB级数对应理论频率构成的频率区间f_i∈[f_m-1,f_m+1)上，频率估计的最大差值与最小差值的平均值定义为中心误差频率f_cen，通过计算该区间上的中心误差频率来进行估计频率修正，依次计算LFB级数的最大值并进行参数估计，直到不含明显的LFB级数最大值为止。

所述中心误差频率的计算分为三步：第一步，计算信号对应的最大项LFB系数，通过LFB系数的幅值最大项计算估计频率第二步，选择第m-1项和第m+1项LFB级数，并计算它们对应的理论频率f_m-₁和f_m+1；第三步，选择合适的步长，计算频率区间上f_i∈[f_m-1,f_m+1)各自的LFB系数幅值最大项对应的估计频率并做如下计算

f_cen即为中心误差频率；因此，修正的估计误差频率为

修正后，估计误差频率满足f_bias≤Δf_m/2。

本发明在贝塞尔函数的相关性质分析的基础上，提出一种变换——LFBT，进而基于LFBT完成多分量SFM信号的参数估计，准确地进行各分量SFM信号的分离。

附图说明

图1示出本发明的流程图；

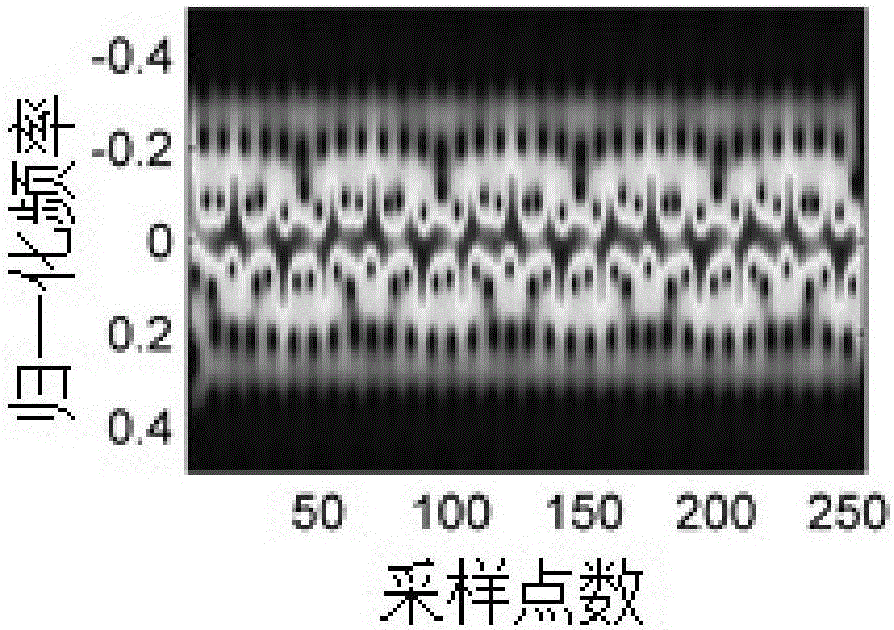
图2示出多分量SFM信号时频分析结果；

图3示出多分量SFM信号的LFB级数；

图4(a)示出第一分量SFM信号时频分析结果，图4(b)示出第二分量SFM信号时频分析结果，图4(c)示出第三分量SFM信号时频分析结果；

图5(a)示出SNR＝8dB条件下，采用不同LFB级数分辨率得到的估计频率归一化均方误差(Normalized Root Mean Square Error,NRMSE)仿真结果；图5(b)示出SNR＝4dB条件下，采用不同LFB级数分辨率得到的NRMSE仿真结果；图5(c)示出SNR＝0dB条件下，采用不同LFB级数分辨率得到的NRMSE仿真结果；图5(d)示出SNR＝-4dB条件下，采用不同LFB级数分辨率得到的NRMSE仿真结果。

具体实施方式

下面结合附图和本发明的实例，对本发明作进一步的描述。

如图1所示，本发明通过下列步骤实现：选择合适的LFB级数分辨率k；计算多分量SFM信号的LFB级数；计算所得频率的相邻两项LFB级数所在区间的中心误差频率，进行频率估计参数的修正；具体说明如下：

第一步：判断多分量SFM信号是否存在相位模糊，若存在则进行相位解模糊处理；

若离散采样信号总相位偏移过大，则会产生相位模糊；由于信号的相位测量值位于区间(-π,π)上，因此当总相位偏移超过2π时产生相位模糊现象；总相位偏移达到2π的整数K倍时，K称为相位模糊数。相位模糊可以通过相邻采样点之间的相位差值进行修正，当相邻采样点之间的相位差值不超过π时，可通过如下方法进行修正

其中pha(n)＝Im[lns(n)]，phar(n)为修正后的相移和测量值之差；因此，当信号相邻采样点的相位差值不超过π时，可进行相位解模糊处理。

第二步：选择合适的LFB级数分辨率k，对解模糊后的多分量SFM信号进行LFBT；

已知正弦调频信号模型为

s(t)＝R exp{j[a sin(ωt)+b cos(ωt)]} (2)

其中R为信号幅度，a、b分别为SFM信号的调制指数，ω为调制频率；

定义信号s(t)的LFBT为

其中J_α(t)为第一类α阶贝塞尔函数，ω为变换域变量。对应的对数傅立叶-贝塞尔逆变换(Inverse Logarithmic Fourier-Bessel Transform,ILFBT)为

在有限区间上傅立叶变换(Fourier Transform,FT)表现为傅立叶级数，与傅立叶变换相似，LFBT在有限区间上以LFB级数(LFB Series)表示；在实际信号处理中，实际信号通常经过离散采样，离散信号的LFB级数表现为信号相位项上的有限项之和

其中n＝1,…,N，N为信号采样点数，t_s为信号采样间隔且N＝T/t_s；第m项LFB系数计算为

其中系数K₁＝2/(N²t_s)为一虚常数,系数随LFB级数项数m变化；由于第α阶贝塞尔函数的正根构成常数列{J_α,m}，因此{K_2,m}也为一不随信号变化的常数列，通常取α＝0；

LFB级数项数与SFM信号的频率调制成分一一对应，第m项LFB级数在频率成分为f_m处取得最大值

因此，对SFM信号进行LFBT变换后，以最大幅值项LFB级数作为SFM信号调制频率的估计。

其中

相邻两项LFB级数对应的频率差值，即频率分辨率计算为

若频率分辨率Δf_m越小，则相邻两项LFB级数对应的理论频率值差值减小，则估计误差也会减小；

将LFB级数分辨率k值引入，当LFB级数分辨率为k时

此时频率分辨率为Δf_m＝1/2πkNt_s；随着LFB级数分辨率k的增大，频率分辨率也会增加；此时估计频率为

其中最大项LFB系数为

此时，相邻两项LFB级数的频率分辨率为

第三步：计算相邻两项LFB级数所在区间的中心误差频率，进行估计频率修正，得到各分量的估计频率；

通过最大项(第项)LFB级数计算出SFM信号的估计频率为通常情况下，最大估计误差频率为频率分辨率的一半，为

此时真实频率为相邻两项LFB系数对应理论频率J_0,m/2πT与J_0,m+1/2πT的平均值；然而这种情况仅适用于一个频率成分仅投影在单根谱线或单个级数上(如FT)。在LFB级数中，一个频率成分投影在若干阶贝塞尔级数上，也就是说，f_m在第m项级数取得峰值同时在邻近的若干阶级数上的投影不为零；设LFB级数的第m项与第m+1项幅值相等，则估计频率位于区间f∈(J_0,m/2πT,J_0,m+1/2πT)上；设信号持续时间T＝1s，k＝1，则

考虑到

近似地，以上方程可转化为

考虑基本不等式可得

其中J_0,m+1≠J_0,m。所以当第m项LFB级数与第m+1项LFB级数幅值相等时，估计频率将大于两理论频率的平均值；也就是说，实际频率略小于估计频率。因此，最大估计误差满足

因此，我们通过计算相邻两项LFB级数的中心误差频率来寻求一种减小估计误差的方法；将相邻两项LFB级数对应理论频率构成的频率区间f_i∈[f_m-1,f_m+1)上，频率估计的最大差值与最小差值的平均值定义为中心误差频率f_cen，通过计算该区间上的中心误差频率来进行估计频率修正。

中心误差频率的计算分为三步，第一步，计算信号对应的LFB系数，通过LFB系数的幅值最大项得到估计频率第二步，选择相邻两项，第m-1项和第m+1项LFB级数，并计算它们对应的理论频率f_m-1和f_m+1；第三步，选择合适的步长，计算频率区间上f_i∈[f_m-1,f_m+1)各自的LFB系数幅值最大项对应的估计频率并做如下计算

即为中心误差频率f_cen；因此，修正的估计误差频率为

修正后，估计误差频率满足f_bias≤Δf_m/2。

最后，依次计算LFB级数的最大值并进行参数估计，直到不含明显的LFB级数最大值为止。

实例：多分量SFM信号参数估计方法

仿真实验：设多分量SFM信号模型为

其中R_i、a_i、f_i分别为信号的幅度、调制系数和调制频率。w(n)为加性高斯白噪声。信号分量参数分别为：分量一：R₁＝2，a₁＝1，f₁＝4.98Hz；分量二：R₂＝2，a₂＝1.5，f₂＝19.47Hz；分量三：R₃＝3，a₃＝2，f₃＝34.19Hz。多分量SFM信号的时频分析结果如图2所示。从图2可以看出，多分量SFM信号在时频域重叠，无法分辨其分量个数以及信号调制频率等信息。

在LFB级数计算过程中，分辨取k＝10。LFB级数计算如图3所示。从图3可以看出，LFB级数分别在第104项、第392项和第688项取得峰值。经计算，三个分量的SFM信号估计频率分别为4.9845Hz、19.4845Hz和34.1845Hz，估计误差为0.0045Hz、0.0145Hz和0.0055Hz。

多分量SFM信号的分解结果如图4(a)、图4(b)、图4(c)分别为分量一、分量二和分量三的时频分析结果。从图上可以看出，时频分析结果清楚的反映了各个分量的时频特征。

图5(a)-图5(d)为不同信噪比和不同LFB级数分辨率条件下，采用200次Monte Carol实验所得的估计频率归一化均方误差(Normalized Root Mean Square Error,NRMSE)仿真结果。结果表明，在相同信噪比条件下，LFB级数分辨率越高，估计频率的NRMSE越小，估计精度越高；在SNR>-4dB条件下，分辨率相同时，信噪比越高估计效果越好。

本发明在贝塞尔函数的相关性质分析的基础上，提出一种变换——LFBT，进而基于LFBT完成多分量SFM信号的参数估计，准确地进行各分量SFM信号的分离。