DTMB中基于校验矩阵的准循环LDPC编码器的制作方法

本发明涉及信道编码领域，特别涉及一种dtmb系统中基于校验矩阵的qc-ldpc编码器。

背景技术：

低密度奇偶校验(low-densityparity-check,ldpc)码是高效的信道编码技术之一，而准循环ldpc(quasi-cyclicldpc，qc-ldpc)码是一种特殊的ldpc码。qc-ldpc码的生成矩阵g和校验矩阵h都是由循环矩阵构成的阵列，具有分块循环的特点，故被称为qc-ldpc码。循环矩阵的首行是末行循环右移1位的结果，其余各行都是其上一行循环右移1位的结果，因此，循环矩阵完全由其首行来表征。通常，循环矩阵的首行被称为它的生成多项式。

dtmb标准采用系统形式的qc-ldpc码，其生成矩阵g的左半部分是一个单位矩阵，右半部分是由e×c个b×b阶循环矩阵gi,j(0≤i<e,e≤j<t,t＝e+c)构成的阵列，如下所示：

其中，i是b×b阶单位矩阵，0是b×b阶全零矩阵。g的连续b行和b列分别被称为块行和块列。由式(1)可知，g有e块行和t块列。dtmb标准采用了一种码率η＝4/5的qc-ldpc码，对于该码，t＝59，e＝48，c＝11，b＝127。

dtmb标准中4/5码率qc-ldpc编码器的现有解决方案是基于c个i型移位寄存器加累加器(type-ishift-register-adder-accumulator,sraa-i)电路的串行编码器。由c个sraa-i电路构成的串行编码器，在e×b个时钟周期内完成编码。该方案需要2×c×b个寄存器、c×b个二输入与门和c×b个二输入异或门，还需要e×c×b比特rom存储循环矩阵的生成多项式。该方案有两个缺点：一是需要大量存储器，导致电路成本高；二是串行输入信息比特，编码速度慢。

技术实现要素：

dtmb系统中4/5码率qc-ldpc编码器的现有实现方案存在成本高、编码速度慢的缺点，针对这些技术问题，本发明提供了一种基于校验矩阵的qc-ldpc编码器。

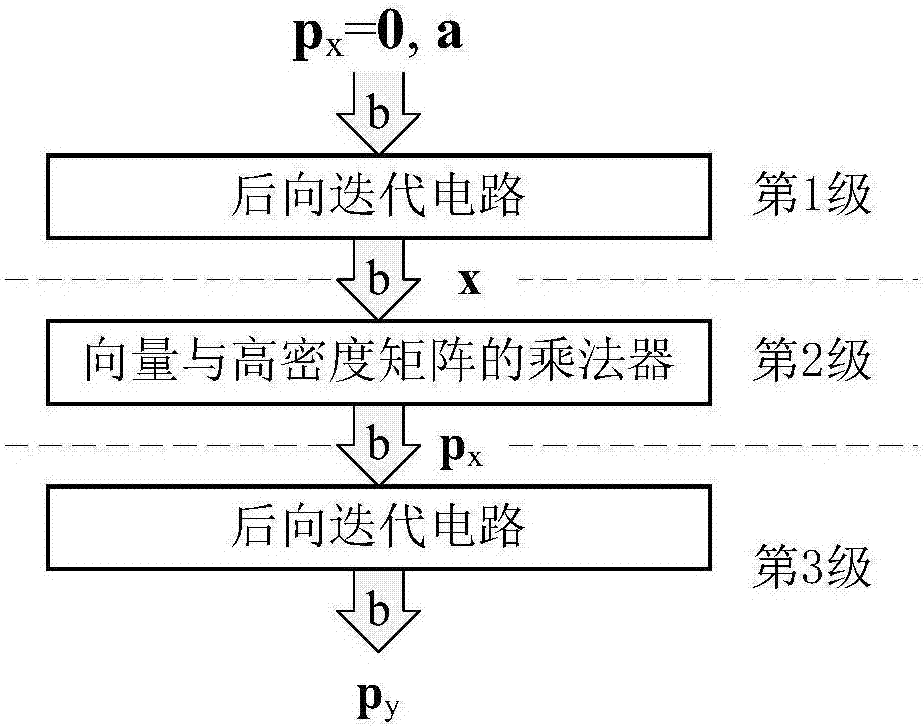
如图2所示，dtmb系统中基于校验矩阵的qc-ldpc编码器主要由2部分组成：后向迭代电路和向量与高密度矩阵的乘法器。编码过程分3步完成：第1步，使用后向迭代电路计算向量py和x；第2步，使用向量与高密度矩阵的乘法器计算部分校验向量px；第3步，使用后向迭代电路计算部分校验向量py，从而得到校验向量p＝(px,py)。

本发明提供的qc-ldpc编码器结构简单，能在显著提高编码速度的条件下，减少存储器，从而降低成本，提高吞吐量。

关于本发明的优势与方法可通过下面的发明详述及附图得到进一步的了解。

附图说明

图1是行列交换后近似下三角校验矩阵的结构示意图；

图2是基于校验矩阵的qc-ldpc编码过程；

图3是后向迭代电路；

图4是循环左移累加器rla电路的功能框图；

图5是由u个rla电路构成的一种向量与高密度矩阵的乘法器；

图6总结了编码器各编码步骤以及整个编码过程所需的硬件资源和处理时间。

具体实施方式

下面结合附图对本发明的较佳实施例作详细阐述，以使本发明的优点和特征能更易于被本领域技术人员理解，从而对本发明的保护范围作出更为清楚明确的界定。

循环矩阵的行重和列重相同，记作w。如果w＝0，那么该循环矩阵是全零矩阵。如果w＝1，那么该循环矩阵是可置换的，称为置换矩阵，它可通过对单位矩阵i循环右移若干位得到。qc-ldpc码的校验矩阵h是由c×t个b×b阶循环矩阵hi,k(1≤i≤c,1≤k≤t,t＝e+c)构成的如下阵列：

通常情况下，校验矩阵h中的任一循环矩阵要么是全零矩阵(w＝0)要么是置换矩阵(w＝1)。令循环矩阵hi,k的首行gi,k是其生成多项式。因为h是稀疏的，所以gi,k只有1个‘1’，甚至没有‘1’。

h的前e块列对应的是信息向量a，后c块列对应的是校验向量p。以b比特为一段，信息向量a被等分为e段，即a＝(a1,a2,…,ae)；校验向量p被等分为c段，即p＝(p1,p2,…,pc)。

对校验矩阵h进行行交换和列交换操作，将其变换成近似下三角形状halt，如图1所示。在图1中，所有矩阵的单位都是b比特而不是1比特。a是由(c-u)×e个b×b阶循环矩阵构成，b是由(c-u)×u个b×b阶循环矩阵构成，t是由(c-u)×(c-u)个b×b阶循环矩阵构成，c是由u×e个b×b阶循环矩阵构成，d是由u×u个b×b阶循环矩阵构成，e是由u×(c-u)个b×b阶循环矩阵构成。t是下三角矩阵，u反映了校验矩阵halt与下三角矩阵的接近程度。在图1中，矩阵a和c对应信息向量a，矩阵b和d对应一部分校验向量px，矩阵t和e则对应余下的校验向量py。p＝(px,py)。上述矩阵和向量满足如下关系：

px^t＝φ(et^-1aa^t+ca^t)(3)

py^t＝t^-1(aa^t+bpx^t)(4)

其中，φ＝(et^-1b+d)^-1，上标^t和^-1分别表示转置和逆。众所周知，循环矩阵的逆、乘积、和仍然是循环矩阵。因此，φ也是由循环矩阵构成的阵列。虽然矩阵e、t、b和d都是稀疏矩阵，但通常情况下φ不再稀疏而是高密度的。

令q^t＝t^–1aa^t，x^t＝eq^t+ca^t以及px^t＝φx^t(或px＝xφ^t)。那么，式(3)和(4)可变为：

和

[abt][apxpy]^t＝0(6)

因为式(5)和(6)中的两个矩阵与t一样都是下三角矩阵，所以式(5)中的x和式(6)中的py都可采用后向迭代的计算方式。

如果px＝0，那么py^t＝t^–1aa^t＝q^t，且式(5)可改写为

其中，

v＝[apxpyx](8)

也就是说，如果px初始化为全零，那么x也可由式(7)计算出来。清零矩阵x对角线上所有的单位矩阵，可得

对比式(10)和图1可见，h′只是比h少了些非零循环矩阵。

式(7)可展开为如下一组等式：

显然，式(6)是式(11)的一部分，因此，式(7)也可用来计算py。

根据以上讨论，可给出一种基于三级流水线的qc-ldpc编码过程，如图2所示。φ涉及向量与高密度矩阵的乘法，而x涉及后向迭代计算。第二级使用向量与高密度矩阵的乘法器实现px＝xφ^t。因为x是下三角矩阵，所以第一级和第三级可使用同种类型的后向迭代电路分别计算x和py。在第一级，px被初始化为全零，py实际上是q；在第三级，px和py是各自的实际值，且无需计算x。

令v＝(v1,v2,…,vt+u)，其中，每一段vk都是v的连续b比特组成，1≤k≤t+u。由式(7)和图1可知，[pyx]＝(vt–c+u+1,vt–c+u+2,…,vt+u)。以vt–c+u+i＝vi′为例，其中，i′＝t–c+u+i,1≤i≤c，t–c+u+1≤i′≤t+u。对于给定的qc-ldpc码，i′与i同步变化。因为下三角矩阵x是从h派生而来，所以hi,i′＝i，且当k>i′时，hi,k＝0。由式(7)可知，x的第i块行与v^t的乘积满足

非零循环矩阵hi,k相对于b×b阶单位矩阵的循环右移位数是si,k，其中，0≤si,k<b，假设在h′的第i块行中有n个非零循环矩阵，它们的块列号分别是k1、k2、…、kn，且1≤k1<k2<…<kn<i′。那么，式(12)变为

或者说

其中，上标^rs(s)和^ls(s)分别表示对矩阵(或向量)循环右移或循环左移s位。

如果vi′按照i′升序依次由式(14)计算，那么py和x可逐段计算出来。该后向迭代过程可由图3所示电路加以实现。该后向迭代电路由1个桶形移位器、3个累加器、2个延时器、2个比较器、1个复用器、1块只读存储器(rom)和1块随机访问存储器(ram)组成。在图3中，桶形移位器采用二分结构和流水线机制，固有延时是τ个时钟周期，其中，τ＝{log2b}表示τ是不小于log2b的最小整数。桶形移位器对一个b比特数循环左移若干位，累加器1对桶形移位器的输出进行累加。如图3所示，h′中所有非零循环矩阵，即h1,k1、h1,k2、…、h1,kn、h2,k1、h2,k2、…、hi,kn、hi+1,k1、…、hc,kn的块列号和移位数逐块行地存储于rom中。通常，hi,kn的下标kn大于hi+1,k1的下标k1。因此，当rom输出的源地址k变小时，式(14)中目的地址i′和块行号i应同时加1。与此同时，累加器1的内容，即目的操作数vi′被写入ram中，然后被清零，以便计算下一个目的操作数。延时器1延时1个时钟周期，它与比较器1配合判断k是否变小。延时器2延时τ个时钟周期是为了补偿桶形移位器的固有延时。累加器3产生目的地址i′。ram根据rom输出的源地址k输出源操作数vk，把目的操作数vi′写入目的地址i′。

从理论上讲，在式(14)中，源地址k一定小于目的地址i′。实际上，由于延时器2延时τ个时钟周期，可能会出现k≥i′。当出现这种情况时，ram输出的vk是无效的，这是因为vi′还未计算出来，更不要说vk。当k≥i′时，rom暂停输出新数据，且送入桶形移位器的数不是vk而是0。根据比较器2的输出，累加器2产生rom的地址，复用器从vk和0中二选一送给桶形移位器。

在第三级，如果b的前r块列是全零，那么py的前r段也无需计算，这是因为这些段恰好等于第一级计算出来的py的前r段。又因为在第三级无需计算x，故在第三级无需使用h′的前r块行和后u块行。假设在h′中及其中间的(c–r–u)块行分别有α和β个非零循环矩阵。由于存在路径延时，在第一和第三级计算x和py所花的总时间下限是(α+β+2τ)个时钟周期。对于dtmb系统中的4/5码率qc-ldpc码，α和β分别是276和225。

如果只考虑图3中rom、ram、桶形移位器和累加器1等主要组成部分的资源消耗，那么该后向迭代电路需要τb个触发器、b个二输入异或门、(t+u)b比特的ram和({log2t}+{log2b})β比特的rom。

使用后向迭代电路计算向量py和x的步骤如下：

第1步，清零累加器1和累加器2，初始化累加器3为i′＝t–c+u+1；

第2步，rom根据累加器2产生的地址输出源地址k及移位数si,k；

第3步，ram根据源地址k输出源操作数vk，比较器2判断源地址k是否小于目的地址i′，若k<i′，则比较器2输出1，否则，比较器2输出0，延时器1与比较器1配合判断k是否变小，若变小，则比较器1输出1，否则，比较器1输出0，累加器3对延时τ个时钟周期的比较器1输出进行累加，产生目的地址i′；

第4步，根据比较器2的输出，累加器2产生rom地址，复用器从vk和0中二选一送给桶形移位器，若比较器2的输出是1，则累加器2递增rom地址，复用器把vk送给桶形移位器，否则，累加器2保持rom地址不变，复用器把0送给桶形移位器；

第5步，桶形移位器对复用器的输出循环左移si,k位，累加器1对桶形移位器的输出进行累加，当延时器2的输出为1时，累加器1的内容即为目的操作数vi′，vi′被写入ram的目的地址i′中，与此同时，累加器1被清零，以便计算下一个目的操作数；

第6步，重复步骤2～5，直到[pyx]＝(vt–c+u+1,vt–c+u+2,…,vt+u)逐段存储于ram中。

由式(7)、图1和v＝(v1,v2,…,vt+u)可知，px＝(vt–c+1,vt–c+2,…,vt–c+u)和x＝(vt+1,vt+2,…,vt+u)。px^t＝φx^t等价于px＝xφ^t。令x＝(x1,x2,…,xu×b)。定义u比特向量sn＝(xn,xn+b,…,xn+(u-1)×b)，其中1≤n≤b。令φj(1≤j≤u)是由φ^t的第j块列中所有循环矩阵生成多项式构成的u×b阶矩阵。则有

vt-c+j＝(…((0+s1φj)^ls(1)+s2φj)^ls(1)+…+sbφj)^ls(1)(15)

由式(15)可得到一种循环左移累加器(rotate-left-accumulator，rla)电路，如图4所示。查找表的索引是u比特向量sn，查找表lj事先存储可变的u比特向量与固定的φj的所有可能乘积，故需2^ub比特的只读存储器(read-onlymemory，rom)。b比特寄存器r1,r2,…,ru分别用于缓冲向量x的向量段vt+1,vt+2,…,vt+u，b比特寄存器ru+j用于存储px的校验段vt–c+j。1个rla电路计算向量vt–c+j需要b个时钟周期。

对于dtmb系统，使用u＝2个rla电路同时计算px＝(vt–c+1,vt–c+2,…,vt–c+u)是一种合理方案，如图5所示的向量与高密度矩阵的乘法器。向量与高密度矩阵的乘法器由u个查找表l1,l2,…,lu、2u个b比特寄存器r2,1,r2,2,…,r2,2u和u个b位二输入异或门x2,1,x2,2,…,x2,u组成。查找表l1,l2,…,lu分别存储可变的u比特向量与固定的矩阵φ1,φ2,…,φu的所有可能乘积，寄存器r2,1,r2,2,…,r2,u分别用于缓冲向量x的向量段vt+1,vt+2,…,vt+u，寄存器r2,u+1,r2,u+2,…,r2,2u分别用于存储px的校验段vt–c+1,vt–c+2,…,vt–c+u。u个rla电路需使用ub个二输入异或门，2^uub比特的rom和2ub个寄存器。u个rla电路计算向量px需要b个时钟周期。使用向量与高密度矩阵的乘法器计算向量px的步骤如下：

第1步，清零寄存器r2,u+1,r2,u+2,…,r2,2u，输入向量段vt+1,vt+2,…,vt+u，将它们分别存入寄存器r2,1,r2,2,…,r2,u中；

第2步，寄存器r2,1,r2,2,…,r2,u同时循环左移1次，异或门x2,1,x2,2,…,x2,u分别对查找表l1,l2,…,lu的输出和寄存器r2,u+1,r2,u+2,…,r2,2u的内容进行异或，异或结果被循环左移1次后分别存回寄存器r2,u+1,r2,u+2,…,r2,2u；

第3步，重复第2步b-1次，完成后，寄存器r2,u+1,r2,u+2,…,r2,2u存储的内容分别是校验段vt–c+1,vt–c+2,…,vt–c+u，它们构成了部分校验向量px。

本发明提供了一种基于校验矩阵的qc-ldpc编码方法，适用于dtmb系统中的4/5码率qc-ldpc码，其编码步骤描述如下：

第1步，使用后向迭代电路计算向量py和x；

第2步，使用向量与高密度矩阵的乘法器计算部分校验向量px；

第3步，使用后向迭代电路计算部分校验向量py，从而得到校验向量p＝(px,py)。

图6总结了编码器各编码步骤以及整个编码过程所需的硬件资源消耗和处理时间。

从图6不难看出，流水线充满时，整个编码过程大约共需max(α+τ,b,β+τ)＝293个时钟周期，远小于基于c个sraa-i电路的串行编码方法所需的e×b＝6096个时钟周期。

dtmb标准中4/5码率qc-ldpc编码器的现有解决方案需要e×c×b＝67056比特rom，而本发明需要({log2t}+{log2b})(α+β)+2^uub＝8179比特rom。

综上可见，与传统的串行sraa法相比，本发明具有编码速度快、存储器消耗少等优点。

以上所述，仅为本发明的具体实施方式之一，但本发明的保护范围并不局限于此，任何熟悉本领域的技术人员在本发明所揭露的技术范围内，可不经过创造性劳动想到的变化或替换，都应涵盖在本发明的保护范围之内。因此，本发明的保护范围应该以权利要求书所限定的保护范围为准。