一种自适应变增益快速响应锁相环改进方法与流程

本发明涉及自适应变增益的锁相环改进方法，用于实现系统快速响应。

背景技术：

随着电力电子技术的飞速发展，锁相环在其中担任的角色越来越重要。锁相环的特点是利用外部输入的参考信号控制环路内部振荡信号的频率和相位，达到电子设备的外部输入信号与内部的震荡信号同步的目的。这个技术在数据采集系统中非常有用，因为通过锁相环，可以使得不同的数据采集板卡共享同一个采样时钟，从而采样时钟也是同步的，准确性大幅度提高。另一方面，锁相环的鉴相环节利用的方式实现，当外部输入信号为小信号时，偏差的角度e趋向于零，此时的sine与e几近重合，可以近似为线性，锁相精准，动态响应迅速。但是，当外部输入信号为大信号时，偏差的角度e较大，sine不能忽略，此时的sine的非线性程度较大，截止频率ωc减小，带宽的实际值比理论值小，锁相环系统的过渡时间增长，相应的动态响应速度变慢。

如申请号201510834014.8的专利一种快速三相电压锁相环方法及其动态响应性能分析方法，包括如下步骤：第一步，对三相电网电压采样,然后通过坐标变换得到两相旋转坐标系下电压分量；第二步，根据开环传递函数、采样频率和基波角频率得到班调节器参数变化的根轨迹；第三步，根轨迹通过闭环主导极点的方法将高阶系统等效简化成为典型二阶系统,得到两种三相电压锁相环对应的阻尼系数；第四步，根据阻尼系数分别得到两种电压锁相环对应的典型二阶系统的收敛时间；第五步，分别计算两种三相电压锁相环的对应的曲线在过零点处的斜率，并根据两曲线的斜率比较两三相电压锁相环达到稳态的时间。

如申请号201510227128.6的专利基于滑动滤波器的锁相环动态性能改进方法，步骤包括：将三相电压ua、ub、uc通过clark变换和park变换转换为两相电压ud、uq。将获得的ud求微分后除以角频率参数,然后再与uq相加得到，将uq的求微分后除以角频率参数,然后再与ud相加得到；将通过滑动滤波器后得到基波正序电压幅值；将通过滑动滤波器后再通过调节器,调节器的输出加上预设角频率后得到锁相环测得的电网电压角频率，进行积分得到锁相环测得的电网电压相位，并将其反馈回输入端完成闭环控制。

技术实现要素：

针对上述现有的技术问题，本发明利用一种自适应变增益快速响应锁相环的改进方法。该方法的实现是根据锁相环系统开环带宽，构建自适应积分增益，降低系统的非线性化程度，提高系统的响应速度，并通过仿真验证了本申请提出方法的有效性和正确性。

为实现上述目的，本发明的具体方案如下：

自适应变增益快速响应锁相环改进方法，包括以下步骤

步骤一：将三相静止坐标系中的电压ua、ub、uc转换为两相旋转坐标系中电压ud、uq；

步骤二：基于同步坐标系的锁相环（srf-pll）非线性数学模型，得到含非线性鉴相环节的锁相环开环传递函数；

步骤三：根据步骤二得到的传递函数的开环截止频率ωc与输入偏差e的关系，构建变增益函数f(e)；

步骤四：利用步骤三中的变增益函数f(e)改造传统pi控制器，设计自适应积分增益代替原有的ki，得到自适应变增益锁相环系统；

步骤五：建立系统闭环等效线性模型，并进行时域分析。

其中，步骤一中利用clark变换将三相静止坐标系中的电压ua、ub、uc转换为两相直角坐标系中电压uα、uβ，具体公式如下：

然后利用park变换将uα、uβ转换为两相旋转坐标系下的ud、uq，

其中为锁相环的输出角度反馈。

在步骤二中，建立的基于同步坐标系的锁相环（srf-pll）非线性数学模型。因为在三相静止坐标系中的电压转换为两相旋转坐标系中电压过程中，锁相环的鉴相环节利用的方式实现，因此系统模型存在非线性部分：，为角度偏差，θ为a相电网电压角度,为同步坐标系下的电压矢量幅值。。

根据锁相环的非线性模型，得到非线性开环传递函数为

式中；

k(e)为非线性增益，随输入偏差变化而变化。

根据步骤二中的传递函数得到开环截止频率ωc：

将鉴相环节对输入偏差的影响考虑成为变增益项，利用频域分析截止频率ωc；通过利用幅值a、非线性系统偏差e与线性系统偏差uq构建变增益函数f(e)，该函数含输入角度及相关非线性信息，用于抵消系统非线性度。

式中，kc为调节系数。

本发明是利用变增益函数对传统pi控制器中的积分常数进行改造。

式中，ki为原锁相环系统的积分增益。

在步骤五中建立的系统闭环等效线性模型时的闭环传递函数如下：

自然频率ωn与阻尼系数的关系式如下：

自适应积分增益明显小于传统锁相环的积分增益ki，因此当代替ki时，阻尼系数增大，自然频率相应减小，但是ωn减小速度跟不上增大的速度，因此衰减系数增大，衰减速度变快，系统从初始状态到达最终状态的响应过程变快。利用偏差与系统阻尼系数的关系。二阶系统的超调量只与阻尼系数有关，在欠阻尼情况下，阻尼系数与超调量呈反比关系，阻尼越大，超调量越小，反之亦然。因此在偏差较大情况下，通过调整调节系数kc，尽可能增大欠阻尼系数，增大衰减速度，降低系统的超调量，系统振荡性降低，系统平稳性转好。

与传统锁相环性能相比，本发明实现了显著的改进。在0度~180度之间，自适应积分增益已经能够降低相位稳定时间，略微提高了大振幅跳变的稳定时间，限制了大的频率偏差。总得来说，增大了锁相环的带宽，降低了系统的非线性度，等效提高了阻尼系数，降低了系统超调量，提高了系统的动态响应速度。

附图说明

图1锁相环的数学模型框图。

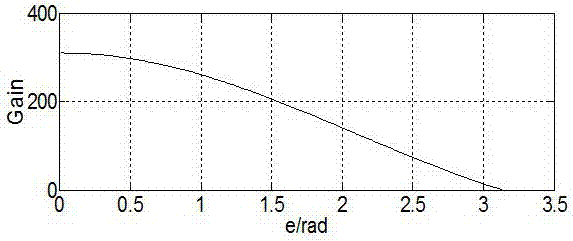
图2锁相环中截止频率ωc与偏差e的关系实验图。

图3锁相环中与偏差e的关系实验图。

图4新型锁相环结构框图。

图5传统锁相环与新型锁相环的截止频率实验对比图。

图6新型锁相环与传统锁相环动态响应时间的实验对比图。

具体实施方式

为了使本发明的实验目的与优点更加清晰明了，下面结构附图说明，进一步详细解释说明：图1是锁相环的结构图，首先是将三相电压ua、ub、uc经过clarke变换转换为uα、uβ,再利用park变换将uα、uβ转换为ud、uq

1、为锁相环的输出角度反馈，θ为a相电网电压角度，为角度偏差；，其中为同步坐标系下的电压矢量幅值。

在非线性数学模型中，鉴相环节利用

的方式实现，因此系统模型存在非线性部分：，该项存在于系统前向通道中。根据锁相环的非线性模型得到该系统的开环传递函数，公式如下：

图2是锁相环中截止频率ωc与偏差e的关系实验图，根据图1中的非线性开环传递函数可以得到截止频率ωc的具体表达式，公式如下：

根据截止频率ωc的公式，将鉴相环节对输入偏差的影响考虑成为变增益项，分别利用截止频率ωc与偏差e的关系曲线和变积分常数与偏差e的关系曲线得到截止频率ωc和变积分常数的关系。

图3是锁相环中与偏差e的关系实验图，根据图2和截止频率ωc的公式明显发现与截止频率ωc关系密切。

在偏差e趋向于0时，极限趋于1，此时uq趋于0，趋于，但是偏差e较大时，uq增大，锁相环系统的非线性度增大，因此利用作为变积分常数，将锁相环系统的偏差控制在无穷小，趋于0的状态。

图4是新型锁相环结构框图，该与传统锁相环结构图相比多了一个非线性积分增益。根据图2截止频率ωc与偏差e的关系和图3变积分常数与偏差e的关系得到截止频率ωc与的关系，在此基础上构建含幅值a、非线性系统偏差e与线性系统偏差uq的变增益函数f(e)。

该函数含输入角度及相关非线性信息，用于抵消系统非线性度。

图5是传统锁相环与新型锁相环的截止频率实验对比图。

利用变增益函数f(e)构建新的自适应积分增益代替原有的积分增益ki:

对传统的锁相环的截止频率ωc进行改进为，公式如下

图6是新型锁相环与传统锁相环动态响应时间的实验对比图，利用变增益函数f(e)改造传统pi控制器，设计的自适应积分增益代替原有的ki，得到自适应变增益锁相环系统。减小开环系统的非线性度，降低角速度与角度间的耦合关系，实现锁相环动态过渡时间的降低。