一种基于树型结构的非均匀滤波器组滤波方法与流程

本发明属于滤波器组技术领域，具体涉及一种基于树型结构的非均匀滤波器组滤波方法。

背景技术：

多通道滤波器组理论被广泛应用在雷达、语音、图像等信号处理领域中，该技术的使用有效地降低了数据处理速率要求、数据存储空间、运算复杂度等。一个滤波器组系统可以通过系统前端分析模块中多个不同频带特性的滤波器对输入信号进行频带划分，之后抽取降速，然后根据实际需要对不同频带的子带信号进行处理。随后在系统后端通过插值以及相应的综合滤波器组将子带信号尽可能地重构成所需的原始信号，因此整个滤波器组的重构性能是滤波器组理论中的研究重点。

滤波器组是多速率信号处理中的一个重要内容，近年来得到广泛重视。滤波器组被广泛应用于通信、语音编码、音频编码和图像信号处理。如果系统的输出和输入的差别只是幅度成比例和存在一定的延时，这个系统就被称为完全重构的系统。将信号分解成子带后处理，便于利用信号的频率特性得到更好的效果。在由分析滤波器组和综合滤波器组构成的系统中，使输出端重构的信号与输入端的原始信号相同，通常是滤波器组设计追求的目标。然而从实用角度考虑，在失真控制在一定范围内的条件下，限制少、效率高、简便的设计方法更有价值。多速率信号处理在通信、图像编码、语音编码、雷达等许多领域都有广泛的应用。多速率技术可以有效降低信号的处理复杂度、数据的传输率和存储量。

非均匀滤波器组可以根据实际需要将输入信号分割为不同频带宽度的子信号，具有更好的灵活性。与均匀滤波器组相比，非均匀滤波器组由于划分频谱更灵活，所以，近年来对非均匀滤波器组的设计研究引起了众多学者的关注，许多学者在非均匀滤波器组的理论和设计方面做出了不少的贡献。但到目前为止，实现非均匀滤波器组的完全重构仍然是设计难题。由于优化的参数较多，设计完全重构的非均匀滤波器组是比较困难的，完全重构的设计方法繁琐、复杂且不容易实现，因此在非均匀滤波器组的实际设计中，一般选取灵活、简单的近似重构设计方案。nguyen等人在《signalprocessingieeetransactionson》上发表的文献《asimpledesignmethodfornearperfectreconstructionnonuniformfilterbanks》中提出了采用合并均匀滤波器组的方法设计非均匀滤波器组。xiex在《circuitsandsystems》上发表的《asimpledesignmethodoflinear-phasenonuniformfilterbankswithintegerdecimationfactors》文献中直接从频域推导非均匀滤波器组的重构关系，并以此设计非均匀滤波器组。soni在文献《anoptimizeddesignofnon-uniformfilterbankusingblackmanwindowfamily》(internationaljournalofsignal&imageprocessing)中采用树型结构设计非均匀滤波器组，同样kumar在文献《designofnearlyperfectreconstructednon-uniformfilterbankbyconstrainedequiripplefirtechnique》(appliedsoftcomputing)中也采用树型结构设计非均匀滤波器组，并简化了迭代目标函数。以上的非均匀滤波器组构造方案存在混叠误差、幅度失真、或相位失真等问题，整个系统的重构性能有待提高。

技术实现要素：

本发明的目的在于提供一种解决现有的非均匀滤波器组构造方案无法设计出具有良好重构性能的非均匀滤波系统问题的基于树型结构的非均匀滤波器组滤波方法。

本发明的目的是这样实现的：

一种基于树型结构的非均匀滤波器组构造方法，包含如下步骤：

第一步：设定原型滤波器的具体参数，其中包括系数长度n，通带截止频率wp、阻带截止频率ws、初始迭代步长step、迭代终止误差recei；

第二步：采用离散加权平方误差准则设计原型滤波器hl(n)，然后求解hl(n)的频率响应在正交镜像点w＝0.5π处的值real；

第三步：判断实际误差是否小于设定的终止误差recei，即以下公式是否成立：

|real-0.7071|＜recei(1)

如果上式成立，则采用该滤波器hl(n)求解出hh(n)，然后以双通道标准正交镜像滤波器组搭建树型结构非均匀滤波器组；如果不成立，则进一步判断real与0.707之间的大小：若real＞0.707，则wp＝wp-step,step＝step/2；若real＜0.707，则wp＝wp+step,step＝step/2，每次迭代之后，步长step变为原来的一半；其中，hh(n)表示高通滤波器,hl(n)表示低通滤波器。

第四步：更新通带截止频率wp，然后采用新的wp再次设计低通滤波器hl(n)，依次迭代，直到误差值小于给定的误差范围。

对于一种基于树型结构的非均匀滤波器组滤波方法，通过迭代滤波器通带截止频率，使原型滤波器hl(z)满足推导出的重构条件；在原型滤波器的具体设计过程中，采用离散加权平方误差准则法设计原型低通滤波器。

其中，hl(z)是低通滤波器hl(n)的传递函数。

对于一种基于树型结构的非均匀滤波器组滤波方法，所述的离散加权平方误差准则法包括以下具体过程：

采用加权离散平方误差准则定义误差函数

e(w)＝w(w)[a(w)-ad(w)](2)

其中，e(w)表示ad(w)与a(w)之间的加权误差；ad(w)表示将要逼近的hd(n)的幅度函数，hd(n)表示理想滤波器；a(w)表示h(n)的幅度函数，h(n)表示实际设计的滤波器；w(w)≥0是加权函数。

加权离散平方误差δ定义为：

其中，(wm,m＝1,2,...,l)是频域中l个采样点。

采用如下形式表示fir滤波器的幅度函数，即：

a(w)＝q(w)g(w)(4)

其中：

其中，q(w)＝cos(w/2),k＝(n-1)/2，n是设计的滤波器阶数。

通过优化的思想求解出中间系数g(n)(n＝1,2,...,k)，再根据以下公式求解出实际系数h(n)的前一半，之后通过对称性，求解出实际需要的fir滤波器的所有系数h(n)。

其中，n＝1,2,...,k-1。

将公式(4)、(5)代入公式(3)中，得：

现将误差函数δ表示为矩阵形式，定义误差向量λ：

λ＝(λ1,λ2,…,λl)^t(8)

其中：

则总误差函数δ可以表示为：

δ＝λ^tλ(10)

采用矩阵形式，误差向量λ可以表示为：

λ＝w(qcg-ad)(11)

其中w和q是l×l的矩阵，即：

c是l×(k+1)的矩阵，即：

ad是l个元素的向量，即：

ad＝[ad(w1),ad(w1),…,ad(wl)](15)

当l＝k+1时，因为wqc是一个l×l矩阵，所以由公式(11)可知，可以通过解方程wqcg＝wad求出误差δ等于零的解。由于误差δ等于零，所以此时的加权矩阵w对实际设计的滤波器没有起到作用。当l＞k+1时，此时方程组的个数大于未知量的个数，故方程组无解，如果此时wqc矩阵是列满秩矩阵，则公式(11)所示的误差函数δ存在唯一的最小解。此时可以通过解如下方程，即：

(wqc)^twqcg＝(wqc)^twadwqc(16)

求解出中间系数向量g，进而通过公式(6)求解出实际设计的单位脉冲响应h(n)。

所述双通道fir标准正交镜像滤波器组基于树型结构的非均匀滤波器组滤波方法，具体设计步骤为：

步骤1：设计双通道fir标准正交镜像滤波器组；

步骤2：以双通道fir标准正交镜像滤波器组为基础模块，结合树型结构搭建非均匀滤波器组；

步骤3：对该方法设计的非均匀滤波器组重构条件进行推导；

步骤4：将整个非均匀滤波器组的重构条件简化为：原型fir滤波器的频率响应在正交点w＝π/2处的幅值满足hl(e^jπ/2)＝0.7071；

步骤5：采用迭代原型滤波器的通带截止频率使其满足步骤4中的重构条件；

步骤6：在原型滤波器的具体设计过程中，采用离散加权平方误差准则法设计原型低通滤波器。

对于一种基于树型结构的非均匀滤波器组滤波方法，双通道fir标准正交镜像滤波器组搭建树型结构的非均匀滤波器组包括分析模块和综合模块。

分析模块中低通道滤波器hl(z)和高通道滤波器hh(z)关系条件设置为：

hh(z)＝hl(-z)(17)

其中，hl(z)，hh(z)分别是分析模块中第一通道和第二通道的传递函数。

综合模块与分析模块中的滤波器关系设置为：

fl(z)＝hh(-z),fh(z)＝-hl(-z)(18)

其中，fl(z)，fh(z)分别是综合模块中第一通道和第二通道的传递函数。

对于一种基于树型结构的非均匀滤波器组滤波方法，采用双通道fir标准正交镜像滤波器组搭建的树型结构非均匀滤波器组的重构条件为：

其中，hk(e^jw)表示第k个通道的滤波器频率响应，w是频率点，π是圆周率，m表示非均匀滤波器组的通道个数。

本发明的有益效果在于：与已有的设计方案相比，本发明简化了迭代重构条件，并且将离散加权平方误差准则应用到树型结构搭建的非均匀滤波器组的设计中，使得整个滤波系统在保证各通道线性相位的同时，各通道的阻带衰减和整个系统的幅度失真都得到了进一步的改善，进而提高了非均匀滤波器组的重构性能。

附图说明

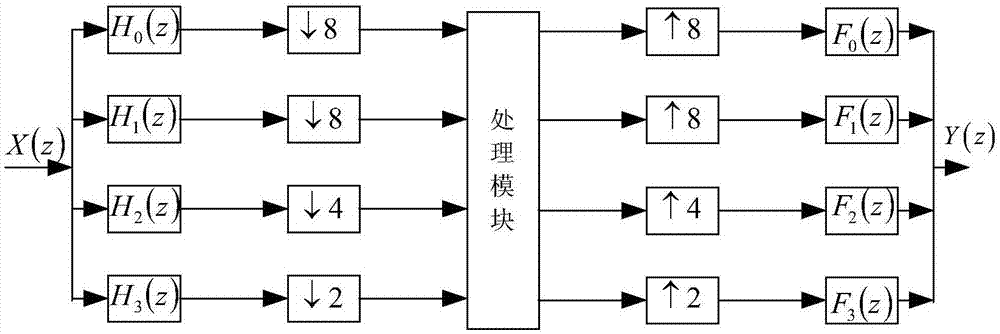
图1是本发明树型结构4通道非均匀滤波器组；

图2是本发明树型结构4通道等效图；

图3是本发明中使用窗函数法、特征滤波法、等波纹法、离散加权平方误差准则等不同方法设计出的fir滤波器的性能对比图；

图4是本发明非均匀滤波器组迭代算法流程图；

图5是本发明原型fir滤波器幅度响应曲线；

图6是本发明树型结构6通道非均匀滤波器组仿真图；

图7是本发明树型结构6通道非均匀滤波器组幅度失真图。

具体实施方式

下面结合附图说明，对本发明中的设计方案进行具体介绍：

步骤1：采用双通道fir标准正交镜像滤波器组搭建树型结构的非均匀滤波器组，图1是本发明树型结构4通道非均匀滤波器组，图2是本发明树型结构4通道等效图，在双通道滤波系统中，分析模块中低通道滤波器hl(z)和高通道滤波器hh(z)关系条件设置为：

hh(z)＝hl(-z)(1)

综合模块与分析模块中的滤波器关系设置为：

fl(z)＝hh(-z),fh(z)＝-hl(-z)(2)

此时整个系统无混叠失真和相位失真。

步骤2：图2中各通道滤波器可以表示为：

且

其中，h0(z)，h1(z)，h2(z)，h3(z)分别为图2中各通道传递函数。

步骤3：此时图2中的非均匀滤波器组重构条件为

其中，hk(e^jw)表示第k个通道的滤波器频率响应。

步骤4：将公式(3)、(5)代入重构条件(6)化简可得：

|hl(e^jw)|⁶+|hl(e^jw)|⁴|hl(e^j(π-w))|²+|hl(e^jw)|²|hl(e^j(π-w))|²+|hl(e^j(π-w))|²＝1(7)

在公式(7)中，取正交频率点w＝π/2进行化简得：

2|hl(e^jπ/2)|⁶+|hl(e^jπ/2)|⁴+|hl(e^jπ/2)|²＝1(8)

求解高阶方程(8)，解得：

hl(e^jπ/2)＝0.7071(9)

将树型结构构成的非均匀滤波器组的通道个数推广到m个，各通道抽取插值速率设为(2^m-1,2^m-1,2^m-2,…,4,2)，等效后的非均匀滤波器组分析模块中各通道系数可以表示为：

且

将公式(10)、(11)所包含的系数关系代入m通道重构条件表达式(6)中，可得：

用e^jw代替上式中的z，且取正交频率点w＝π/2对其进行化解，得：

2|hl(e^jπ/2)|^2(m-1)+hl(e^jπ/2)|^2(m-2)+|hl(e^jπ/2)|^2(m-3)+…+|hl(e^jπ/2)|⁴+|hl(e^jπ/2)|²＝1

(13)

解高阶方程(13)得到与公式(9)同样的解hl(e^jπ/2)＝0.7071，所以，采用双通道fir标准正交镜像滤波器组结合树型结构搭建的非均匀滤波器组的重构条件为hl(e^jπ/2)＝0.7071。

采用迭代原型滤波器hl(z)的通带截止频率使其满足重构条件(9)。在具体设计过程中应用离散加权平方误差准则设计原型滤波器hl(z)。该方法采用优化思想使实际设计的滤波器频率响应h(e^jw)无限接近理想频率响应hd(e^jw)，使两者之间的误差最小。与窗函数法、等波纹设法、特征滤波器法相比，在设计参数相同的情况下，离散加权平方误差准则可以得到更加平坦的通频带和更大的阻带衰减。其具体的设计过程如下：首先采用加权离散平方误差准则定义误差函数。

e(w)＝w(w)[a(w)-ad(w)](14)

加权离散平方误差δ定义为：

频率采样点个数l用来表征通带、阻带性能。该方法设计fir滤波器的思想就是使公式(15)定义的误差δ最小。采用如下形式表示fir滤波器的幅度函数，即：

a(w)＝q(w)g(w)(16)

其中：

通过优化的思想，求解出中间系数g(n)(n＝1,2,...,k)，之后再根据以下公式求解出实际系数h(n)的前一半，然后再通过对称性，求解出实际需要的fir滤波器的所有系数h(n)。

其中，n＝1,2,...,k-1。

将公式(16)、(17)代入公式(15)中，得：

现将误差函数δ表示为矩阵形式，定义误差向量λ：

λ＝(λ1,λ2,…,λl)^t(20)

其中：

则总误差函数δ可以表示为：

δ＝λ^tλ(22)

采用矩阵形式，误差向量λ可以表示为：

λ＝w(qcg-ad)(23)

其中，w和q是l×l的矩阵，即：

c是l×(k+1)的矩阵，即：

ad是l个元素的向量，即：

ad＝[ad(w1),ad(w1),…,ad(wl)](27)

当l＝k+1时，因为wqc是一个l×l矩阵，所以由公式(23)可知，可以通过解方程wqcg＝wad求出误差δ等于零的解。由于误差δ等于零，所以此时的加权矩阵w对实际设计的滤波器没有起到作用。当l＞k+1时，此时方程组的个数大于未知量的个数，故方程组无解，如果此时wqc矩阵是列满秩矩阵，则公式(23)所示的误差函数δ存在唯一的最小解。此时可以通过解如下方程，即：

(wqc)^twqcg＝(wqc)^twadwqc(28)

求解出中间系数向量g，进而通过公式(18)求解出实际设计的单位脉冲响应h(n)。

下面分别采用特征滤波器法、等波纹设计法、窗函数设计法、离散加权平方误差准则法设计fir滤波器并将结果做对比分析。图3是本发明中窗函数法、特征滤波法、等波纹法、离散加权平方误差准则性能对比图，具体参数性能如表1所示。

表1不同方法构造fir滤波器具体参数特性对比

通过表1可知，在设计参数相同的情况下，采用离散加权平方误差准则可以实现更大的阻带衰减，进而更好地抑制带外信号。

图4是本发明非均匀滤波器组迭代算法流程图，下面结合图4给出非均匀滤波器组的具体设计步骤：

步骤1：

第一步：设定原型滤波器的具体参数，其中包括系数长度n，通带截止频率wp、阻带截止频率ws、初始迭代步长step、迭代终止误差recei；

第二步：采用离散加权平方误差准则设计原型滤波器hl(n)，然后求解hl(n)的频率响应在正交镜像点w＝0.5π处的值real；

第三步：判断实际误差是否小于设定的终止误差recei，即以下公式是否成立：

|real-0.7071|＜recei(29)

如果上式成立，则采用该滤波器hl(n)求解出hh(n)，然后以双通道fir标准正交镜像滤波器组搭建树型结构非均匀滤波器组；如果不成立，则进一步判断real与0.707之间的大小：若real＞0.707，则wp＝wp-step,step＝step/2；若real＜0.707，wp＝wp+step,step＝step/2，每次迭代之后，步长step变为原来的一半；其中，hh(n)表示高通滤波器。

第四步：更新通带截止频率wp，然后采用新的wp再次设计滤波器hl(n)，依次迭代，直到误差值小于给定的误差范围。

为了验证本发明的有效性，进行了仿真实验。采用本发明设计一个各通道抽取插值速率分别为(16,16,8,4,4,4)的6通道非均匀滤波器组，将迭代终止误差设置为recei＝10^-4以保证良好的精度，迭代步长设置为step＝0.15π。并且定义幅度失真函数amdis来表征整个系统的重构性能，即：

其中，hm(e^jw)表示第m个通道的滤波器频率响应。

原型滤波器hl(n)的具体参数为：系数长度n＝63、通带截止频率为wp＝0.41π，阻带截止频率ws＝0.65π。采用离散加权平方误差准则构造滤波器hl(n)，图5是本发明原型fir滤波器幅度响应曲线，从图5可以看出此时阻带衰减为as＝-133db。图6是本发明树型结构6通道非均匀滤波器组仿真图，图7是本发明树型结构6通道非均匀滤波器组幅度失真图，此时幅度失真的最大值为max(amdis)＝1.3×10^-3。将本发明方法与已有的设计方法进行对比，如表2所示。

表2不同设计方法性能对比

表3本文设计方法与kumar设计法性能对比

由表3可知，与kumar设计法相比，本文的设计方法在阻带衰减方面平均提高了59.6％，在幅度失真方面平均提高了37.6％。综合以上分析可知，将离散加权平方误差准则应用到树型结构搭建的非均匀滤波器组的设计中之后，整个滤波系统在保证各通道线性相位的同时，各通道的阻带衰减和整个系统的幅度失真都得到了进一步的改善，进而提高了非均匀滤波器组的重构性能。