基于MWC的支撑集快速恢复方法与流程

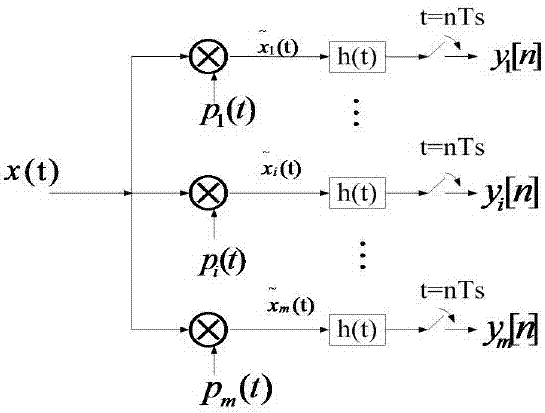
本发明属于盲频谱信号处理与压缩感知交叉的技术领域，具体在于子频带数较少时，构造出一种基于mwc系统的支撑集快速恢复方法。

背景技术：

nyquist采样定理表明，当采样率大于信号最大频率的2倍时，才能完美地恢复出原始信号，否则会产生混叠。目前流行的降采样技术主要包括模拟解调、周期非均匀采样、数字下变频等，但是这些技术并不能从根源上解决采样的瓶颈，直到2006年，压缩感知（cs）理论的产生，在稀疏信号的处理中突破了传统nyquist采样定理的两倍采样率的瓶颈。刚开始时，研究重点是对压缩感知的理论研究，也就是对nyquist采样后的数字信号进行感知恢复的研究，真正的模拟域nyquist欠采样的研究主要有rice大学baraniuk团队随机解调（rd）压缩采样模型以及以色列理工大学eldar团队提出的调制宽带转换器（modulatedwidebandconverter,mwc）模型。随机解调适用于多音信号，它把全频带1hz的频率分辨率细分成很多的频率，然后用恢复算法找到不为0的频率成分，而调制宽带转换器这对宽带稀疏信号模型更加普遍，并且是基于频谱切片的分析思想让后端恢复更加快速。

调制宽带转换器欠采样系统是以色列学者eldar在2010年设计的基于压缩感知的一种欠采样系统，中文名为调制宽带转换器（mwc）。mwc针对盲多频带稀疏信号做的有效的欠采样且能完美恢复出原始信号，因此mwc能够有效降低非合作宽带稀疏信号的采样频率，从而在全频带信号监听与侦查上有得天独厚的优势。由于mwc的信号模型就是将宽带频谱切片进行分段感知，因此完全可以将mwc应用于频谱感知中。而在某些信号的频谱感知中，如调频信号感知中，快速感知是首要的目的，因此研究如何在不大幅度降低重构率的前提下提高mwc的恢复速率是十分有必要的。

mwc的原理框图如图2，mwc的精髓就在于事先利用周期性的伪随机信号与原宽频稀疏信号进行混频，将宽频内的子频带搬移到基带，此时基带中包含了各个子频带的信息，利用低通滤波器滤出低频信号。由于没有高频成分，利用商用的adc器件就完全可以实现均匀采样，采样出来的信息就是压缩采样值，利用压缩感知的恢复原理可以实现支撑集的有效恢复。

在mwc的恢复过程中，需要把模拟域的压缩采样值输入到压缩感知的恢复算法中，才能实现mwc的支撑集恢复，而这个模块就是连续到有限模块（continuoustofinite,ctf）。mwc的原理分析大部分都是基于频域分析的，因为mwc的思想就是将频域分片，然后把不为0的频谱切片找出来进行恢复。但是虽然是基于频域的分析，恢复却是基于时域的恢复，因为频域是无限维的，它的cs模型是imv（infinitemeasurementvectors）模型，因此之间频域恢复是做不到的，但是从有限维的压缩采样值中恢复各个频谱切片的采样值是有可能的，这就是mwc支撑集恢复中的mmv（multiplemeasurementvectors）理论模型。而在ctf恢复模块中有两个地方比较耗时，一个是通过矩阵q来求解矩阵v的过程，因为要经过对矩阵q特征值分解，所以比较耗时，另一个是mwc恢复算法（m-omp），因为采样值矩阵是多列的，会增加恢复时间，因此可以从这两个地方着手以降低恢复的时间。图3为ctf模块耗时分析图。

在ctf模块中，首先将mwc欠采样系统得到的压缩采样值乘以的共轭转置，得到mwc系统m个通道的压缩采样值组成的矩阵q，然后通过对q进行特征值分解得到的矩阵v作为观测值矩阵，进而构造出cs模型，利用cs中的m-omp算法可以找到u的支撑集，最后通过求出原始信号。因为测量值矩阵是多列，在传统的cs模型中，测量值矩阵都是单列的，所以利用m-omp算法对信号进行恢复的过程中，需要做很多次的v与c的内积运算，因此多列的测量值矩阵会增加恢复的时间，如果能找到一种方法，能够减少v的列数而又不丢失测量值的全局信息，则可以在取得近似重构率的前提下减少恢复的时间。

技术实现要素：

本发明旨在针对ctf模块构造多列测量值矩阵造成恢复时间过慢的问题而提出的一种基于mwc的支撑集快速恢复方法，其技术方案如下：

基于mwc的支撑集快速恢复算法，其步骤如下：

步骤一：通过mwc欠采样系统，得到测量值矩阵；

步骤二：将测量值矩阵中n列加为只有2n列的矩阵；

步骤三：利用cs中的m-omp算法恢复出支撑集

图1为基于mwc的支撑集快速恢复算法的框图。

图2为mwc的原理框图。

图3为mwc的ctf模块耗时分析图。

图4支撑集恢复率与信噪比的关系图。

图5恢复时间与通道数的关系图。

图6支撑集恢复率和信噪比及通道数的关系图。

具体实施方式

图1为基于mwc的支撑集快速恢复方法的流程图，本发明的具体实施方案分为三个步骤，结合附图1阐述如下：

步骤一：图2为mwc的原理框图，通过将含有n个子频带的原始信号分别输入到m个通道中，与伪随机序列进行混频，把频带内的频谱信息扩散到整个频带，此时基带内的包含全部的频谱信息，利用低通滤波器滤出基带内的信息，因为没有高频成分，可以用现有的adc采样器等间隔采样得到大小的测量值矩阵，其表达式如下；

步骤二：将测量值矩阵的n列加为只有2n列的矩阵，而不是其他列数的矩阵，例如子频带数n=6时，用n除以2n，向下取整得到k，则在测量值矩阵中，把分别把n列分解为2n个k列，然后把k列加为一列，得到2n列的新测量值矩阵，其表达式如下：

其中m为通道数，n为包含负子频带在内的频带总数,。这样就可以得到少于原测量值矩阵列数的新测量值矩阵，对应的压缩感知，通过这个方法不仅不用经过特征值分解矩阵q的步骤，而且测量值矩阵列数的减少可以提高恢复的速率

步骤三：得到mmv模型之后，利用改进的omp算法恢复的支撑集。其中改进的omp算法步骤如下：

1)initialize：迭代次数t为0，残差r为y，索引集向量为[]；

2)找到残差r与测量矩阵c的内积值最大的索引值，将加到索引集向量中，同时找到对称的频带索引值以及相邻的频谱切片索引值，以及对应的相邻频谱切片值，将其都加入到索引集向量中；

3)用最小二乘法更新原子系数；

4)更新残差，t++；

5)判断t是否满足迭代条件，若不满足，则停止迭代；否则，回到步骤2。

图4为在子频带数n为6，通道数m为50，原方法与新方法在信噪比从-30db到30db时与恢复率之间的关系图。

图5为在子频带数n为6，信噪比为30db，原方法与新方法在通道数从15到50时与恢复时间之间的关系图。

图6的仿真实验为原文章上的经典仿真图，能够同时显示通道数，信噪比，恢复率三者之间的关系，横轴表示通道数，纵轴表示信噪比，最右边的横条表示恢复率，颜色越白表示恢复率越高。