基于DSADC的旋变软件解码系统及其方法与流程

本发明涉及交流伺服控制领域，尤其涉及旋转变压器的编解码领域，具体是指一种基于dsadc的旋变软件解码系统及其方法。

背景技术：

在交流伺服控制系统中，只有获得准确可靠的转子位置和速度信息才可以实现对电机的高性能控制。旋转变压器作为一种十分常见的电磁感应式位置传感器，因结构简单、精度高、抗干扰性强等显著特点被广泛的应用在各种场合。旋转变压器的两路输出信号为幅值随其位置变化的模拟信号，需要通过数字转换处理成数字角度信号才能被计算机或者其他控制器所使用。对旋变输出的模拟信号进行数字转换处理目前市场上比较成熟的技术就是采用专用的解码芯片，专用芯片的使用可以获得较高的解码精度和较好的性能，但是其价格昂贵，在对成本有严格要求的场合难以广泛使用。

在工业应用中，如何能让系统的控制达到高的精度的是一个一直探讨的课题。交流电机作为交流伺服系统的执行部件，在运行的过程中需要获得转子的位置并发送给控制器，以提高闭环系统的控制性能。永磁同步交流电机和感应异步交流电机是目前电动机主要的两大类型，其中永磁同步交流电机具有十分良好的低速性能、能够实现弱磁高速控制，宽广的调速范围、以及极高的效率，因此已经在交流伺服系统中成为了首要的选择。在电动汽车的驱动系统领域，永磁同步电机也随着新能源汽车的推广与发展获得了同步的快速发展。根据永磁同步电机结构可知其运行稳定可靠，但作为无刷电动机的一种它没有换向机构，因此需要位置传感器来确定电机转子的位置、转速等参数。系统的输出结果通过传感器后产生一个负反馈给控制器，然后与系统的输入量与通过进行比较，从而发送控制命令用以指示驱动机和执行电机的行动，由于负反馈的存在系统的输入与输出误差就会得到调整变得越来越小。反馈系统是否能够达到完美的效果，选择高精度高分辨率的传感器是十分重要的。在电机控制环节中电机转子旋转位置是重要反馈部分，它直接影响着电机的工作表现。目前光电编码器和旋变是最为主要的永磁同步交流电机转子位置和速度信号测量元件。

光电编码器的主要特点是体积较小、分辨率极高、安装简单、精度高，由于直接以数字信号作为输出，因此数据的处理电路比较简单，但是为了得到较好的光学信号，光电编码器对光栅的刻画工艺要求高，同时对环境比较敏感，耐冲击及抗振动性比较差，工作环境受到了一定限制。相比较而言，除了拥有相对更小的误差以及更高的精度等特点以外旋变还具有构造简单、坚固耐用，抗干扰能力强等突出优点。由于旋转变压器有众多光电编码器不具备的优点，除了在一般的传感器应用场合外，一些特殊场合，尤其在抗冲击、抗振动，易燃易爆等恶劣环境条件下如军事、航空、航天等要求高可靠性应用的领域也得到了广泛的应用。此外,目前除了在工业、交通行业以外旋转变压器也开始在民用领域得到广泛应用如新能源汽车、数控机床、电力、冶金、纺织等领域。

旋转变压器的两路输出均为模拟信号，对输出数据处理电路要求高结构相对复杂是其在应用中的最大缺点。以正余弦型旋变作为研究对象来讨论，其输出的两路信号为均包含了转子的位置信息的一路正弦信号和另一路余弦信号,如何从其中解算出电机转子位置，获得到转子位置的高精度数字信号是不太容易的，因此分析和研究怎样合适的处理这两路正余弦信号以准确快速地获取高精度的位置信息是十分重要的。针对这一问题，目前很多公司都研发推出了一系列专用的旋变位置解码芯片如美国ad公司开发的ad2s80、ad2s80a、ad2s1200系列和日本多摩川公司的au6802、au6802n1、au6803系列等。专用芯片解码技术比较成熟，但这种芯片的价格一般比较昂贵，将会大大增加系统成本。为了节约成本，弥补这一缺点，本研究拟通过软件算法来进行旋转变压器的位置解码。通过采用基于过采样原理的deltasigmaadc实现对模拟信号的高频精确采样会产生系统的相位滞后，需要在算法中加入延时校正来进行补偿，回路参数条件变化时延时校正补偿可自动调节。对于数字信号中包含的载波信号的解调主要通过反向整形和积分运算实现，解调后的信息再经过最后的观测器算法进行了转子角度信号的实时解算。该解码方法具有高精确度和高动静态性能，可以节约硬件开发成本，避免了资源的浪费，从而创造出更好的经济效益，从而实现了旋转变压器的低成本、高性能、高集成度的角度变换。

目前对旋转变压器主要采用硬件解码的形式，即采用专用芯片实现解码，很少使用软件解码方式。可搜索到的专利中，关于软件解码的有“一种基于旋转变压器软件解码的电动助力转向系统”，其软件解码方式主要分为两部分，首先是对旋转变压器输出的信号进行信号处理，主要是通过硬件电路的方式进行处理，得到包含电机转子位置的正、余弦信号，然后通过cordic算法解算出转子的位置。

具体实现过程为如图1所示，对旋转变压器输出的差分正余弦信号进行滤波，再经过直流偏执以及比例放大后转换为单极性信号，然后使用cordic算法解算出转子位置。

假设某一时刻旋变的旋转角度θ，获取该θ对应的正余弦值后，通过不同的算法从正余弦值中得到直观的角度值。“不同的算法”除了标定查表法以外，还包括反正切法，反正切法是目前较常见的旋变解算方法，首先通过三角函数计算公式tanθ＝sinθ/cosθ获取此时旋转角度θ的正切值，再通过进一步的反正切运算θ＝arctanθ即可得到具体的角度值，得到角度信息值后通过微分运算就能得到电机的转速n。反正切法对硬件配置要求较低，所需的外围硬件电路简单，软件计算对处理器的要求也不高，但是由于旋变的输出信号一般都含有噪声和高次谐波，存在计算量大、抗干扰性差等缺点，使其解码精度不高。

现有的比较成熟的硬件解码方案需要单独购买专用的解码芯片，这种芯片的价格比较昂贵，会使系统成本大大提高，而且精度受限。

上述提到的已有的软件解码方案，需要使用单独的mcu进行软件解码，同时需要单独设计硬件电路对旋转变压器输出信号进行处理，也额外的增加了成本。在信号处理阶段，为了得到所需的正余弦信号，对采样信号进行了低通滤波处理，但是没有对滤波后的结果进行幅值和相位的补偿，这样得到的结果会有偏差。

技术实现要素：

本发明的目的是克服上述现有技术中的缺点，提供了一种低成本的基于dsadc的旋变软件解码系统及其方法。

为了实现上述的目的，本发明的基于dsadc的旋变软件解码系统及其方法具体如下：

该基于dsadc的旋变软件解码系统，其主要特点是，所述的旋变软件解码系统基于主mcu中的dsadc模块，包括以下单元：

高频精确采样单元，用以对旋转变压器输出的模拟信号进行高频精确采样，获取所述的旋转变压器输出的模拟信号经高频精确采样后生成的数字信号；

解调模块，用以对所述的高频精确采样单元输出的旋转变压器输出的数字信号进行解调，获取数字信号中包括的载波信号，输出旋转变压器的旋转角度θ的正弦曲线与余弦曲线；

观测器模块，用以根据所述的解调模块输出的旋转变压器的旋转角度θ的正弦值与余弦值进行转子角度信号的实时解算，获取观测角度和角速度还用以获取观测误差。

较佳地，所述的高频精确采样单元为基于过采样的高频精确采样单元，其过采样率的设置范围为4至512，其a/d模数采样速率范围为10mhz～20mhz。

较佳地，所述的解调模块包括反向整形单元和与所述的反向整形单元相连接的积分运算单元，且所述的解调模块通过所述的反向整形单元连接至所述的高频精确采样单元，通过所述的积分运算单元连接至所述的观测器模块，且

所述的反向整形单元用于进行正负半轴信号的反转；

所述的积分运算单元用于对完成反转后的信号的积分处理，以获取旋转角度θ的正弦曲线和余弦曲线。

较佳地，所述的观测器模块为一基于锁相环的角度观测器模块，其输入端连接所述的解调模块的输出端，用以对输入端输入的旋转变压器的旋转角度θ的正弦值和余弦值进行处理，获取观测角度和角速度所述的观测器模块还根据观测角度和所述的解调模块输出的旋转变压器的旋转角度θ的正弦值、余弦值获取观测误差ε。

更佳地，所述的角度观测器模块的传递函数为：

其中，kp为比例系数，ki为积分系数，且所述的ki由所述的旋转变压器的固有频率ωn确定，所述的kp由所述的旋转变压器的固有频率ωn以及所述的旋转变压器的阻尼因子ξ确定。

尤佳地，所述的ki与所述的kp分别为：

kp＝2ξωn；

其中，所述的ωn为旋转变压器的固有频率，所述的ξ为所述的旋转变压器的阻尼因子。

上述基于dsadc的旋变软件解码系统实现解码的方法，其主要特点是，所述的方法包括以下步骤：

(1)通过所述的高频精确采样单元对所述的旋转变压器输出的模拟信号进行高频精确采样；

(2)通过解调模块对经高频精确采样后获取的数字信号进行解调，获取相应的载波信号，从而获取所述的旋转变压器的旋转角度θ的正弦曲线和余弦曲线；

(3)通过观测模块对步骤(2)中获取的旋转角度θ的正弦值和余弦值进行转子角度信号的实时解算，获取旋转变压器的观测角度和角速度

较佳地，所述的解调模块包括反向整形单元和与所述的反向整形单元相连接的积分运算单元，且所述的解调模块通过所述的反向整形单元连接至所述的高频精确采样单元，通过所述的积分运算单元连接至所述的观测器模块，且所述的反向整形单元用于进行正负半轴信号的反转；所述的积分运算单元用于对完成反转后的信号的积分处理，以获取旋转角度θ的正弦曲线和余弦曲线，且所述的步骤(2)为：

所述的解调模块通过所述的反向整形单元对所述的高频精确采样单元输出的数字信号进行反向整形，并通过所述的积分运算单元对经反向整形的数字信号进行积分运算，获取载波信号，从而获取所述的旋转变压器的旋转角度θ的正弦曲线和余弦曲线，从而获取对应的正弦值和余弦值。

较佳地，观测器模块为一基于锁相环的角度观测器模块，其输入端连接所述的解调模块的输出端，用以对输入端输入的旋转变压器的旋转角度θ的正弦值sinθ和余弦值cosθ获取观测角度和角速度所述的步骤(3)为：

所述的观测器模块对输入端输入的旋转变压器的旋转角度θ的正弦值和余弦值进行处理，获取观测角度和角速度所述的观测器模块还根据观测角度和所述的解调模块输出的旋转变压器的旋转角度θ的正弦值、余弦值获取观测误差ε。

采用本发明的基于dsadc的旋变软件解码系统及其方法，直接利用主mcu中自带的dsadc模块进行软件解码，不需要额外的芯片或者mcu，由于采用基于过采样原理的deltasigmaadc对模拟信号进行高频精确采样会产生系统的相位滞后，在系统中加入延时校正来进行补偿，回路参数条件变化时延时校正补偿可自动调节。对于数字信号中包含的载波信号的解调主要通过反向整形和积分运算实现，解调后的信息再经过最后的观测器模块进行了转子角度信号的实时解算，而相位误差的补偿也由所述的观测器模块实现，具有高精确度和高动静态性能的特点，可以节约硬件开发成本，避免了资源的浪费，从而创造出更好的经济效益，从而实现了旋转变压器的低成本、高性能、高集成度的角度变换，不需要额外的mcu专门进行软件解码，不需要自己单独设计硬件电路对信号进行处理、对信号处理中的滤波等进行补偿、计算转子位置时通过二阶锁相环的结构计算得到转子位置，能够快速准确地得到转子位置，动态响应性能好，抗干扰能力强，稳态时能够消除偏差，明显优于cordic算法。

附图说明

图1为现有技术中实现旋变软件解码的方法流程示意图。

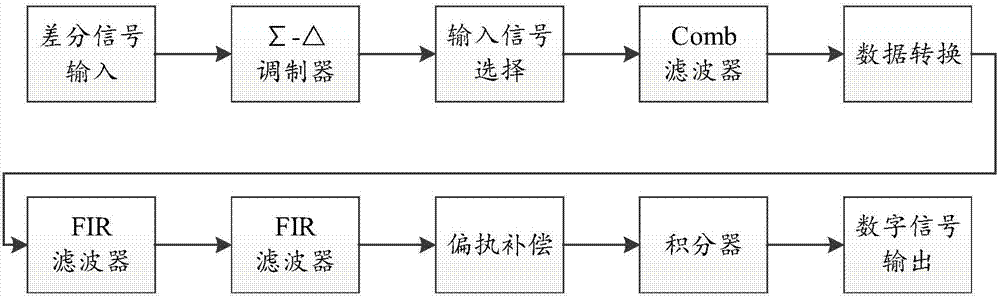
图2为本发明的单片机中的deltasigmaadc模块单元的工作流程示意图。

图3为旋变输出信号经滤波抽取后的信号曲线。

图4为二阶角度跟踪观测器原理框图。

图5为本发明的基于dsadc的旋变软件解码系统的方法流程示意图。

具体实施方式

为了能够更清楚地理解本实用技术内容，特举以下实施例详细说明。

该基于dsadc的旋变软件解码系统，其主要特点是，所述的旋变软件解码系统基于主mcu中的dsadc模块，包括以下单元：

高频精确采样单元，用以对旋转变压器输出的模拟信号进行高频精确采样，获取所述的旋转变压器输出的模拟信号经高频精确采样后生成的数字信号；

解调模块，用以对所述的高频精确采样单元输出的旋转变压器输出的数字信号进行解调，获取数字信号中包括的载波信号，输出旋转变压器的旋转角度θ的正弦曲线与余弦曲线；

观测器模块，用以根据所述的解调模块输出的旋转变压器的旋转角度θ的正弦值与余弦值进行转子角度信号的实时解算，获取观测角度和角速度还用以获取观测误差。

在一种较佳的实施例中，所述的高频精确采样单元为基于过采样的高频精确采样单元，其过采样率的设置范围为4至512，其a/d模数采样速率范围为10mhz～20mhz。

在一种较佳的实施例中，所述的解调模块包括反向整形单元和与所述的反向整形单元相连接的积分运算单元，且所述的解调模块通过所述的反向整形单元连接至所述的高频精确采样单元，通过所述的积分运算单元连接至所述的观测器模块，且

所述的反向整形单元用于进行正负半轴信号的反转；

所述的积分运算单元用于对完成反转后的信号的积分处理，以获取旋转角度θ的正弦曲线和余弦曲线。

在一种较佳的实施例中，所述的观测器模块为一基于锁相环的角度观测器模块，其输入端连接所述的解调模块的输出端，用以对输入端输入的旋转变压器的旋转角度θ的正弦值和余弦值进行处理，获取观测角度和角速度所述的观测器模块还根据观测角度和所述的解调模块输出的旋转变压器的旋转角度θ的正弦值、余弦值获取观测误差ε。

在一种更佳的实施例中，所述的角度观测器模块的传递函数为：

其中，kp为比例系数，ki为积分系数，且所述的ki由所述的旋转变压器的固有频率ωn确定，所述的kp由所述的旋转变压器的固有频率ωn以及所述的旋转变压器的阻尼因子ξ确定。

在一种尤佳的实施例中，所述的ki与所述的kp分别为：

kp＝2ξωn；

其中，所述的ωn为旋转变压器的固有频率，所述的ξ为所述的旋转变压器的阻尼因子。

上述基于dsadc的旋变软件解码系统实现解码的方法，其主要特点是，所述的方法包括以下步骤：

(1)通过所述的高频精确采样单元对所述的旋转变压器输出的模拟信号进行高频精确采样；

(2)通过解调模块对经高频精确采样后获取的数字信号进行解调，获取相应的载波信号，从而获取所述的旋转变压器的旋转角度θ的正弦曲线和余弦曲线；

(3)通过观测模块对步骤(2)中获取的旋转角度θ的正弦值和余弦值进行转子角度信号的实时解算，获取旋转变压器的观测角度和角速度

在一种较佳的实施例中，所述的解调模块包括反向整形单元和与所述的反向整形单元相连接的积分运算单元，且所述的解调模块通过所述的反向整形单元连接至所述的高频精确采样单元，通过所述的积分运算单元连接至所述的观测器模块，且所述的反向整形单元用于进行正负半轴信号的反转；所述的积分运算单元用于对完成反转后的信号的积分处理，以获取旋转角度θ的正弦曲线和余弦曲线，且所述的步骤(2)为：

所述的解调模块通过所述的反向整形单元对所述的高频精确采样单元输出的数字信号进行反向整形，并通过所述的积分运算单元对经反向整形的数字信号进行积分运算，获取载波信号，从而获取所述的旋转变压器的旋转角度θ的正弦曲线和余弦曲线，从而获取对应的正弦值和余弦值。

在一种较佳的实施例中，所述的观测器模块为一基于锁相环的角度观测器模块，其输入端连接所述的解调模块的输出端，用以对输入端输入的旋转变压器的旋转角度θ的正弦值sinθ和余弦值cosθ获取观测角度和角速度所述的步骤(3)为：

所述的观测器模块对输入端输入的旋转变压器的旋转角度θ的正弦值和余弦值进行处理，获取观测角度和角速度所述的观测器模块还根据观测角度和所述的解调模块输出的旋转变压器的旋转角度θ的正弦值、余弦值获取观测误差ε。

请参阅图4，在一种具体实施例中，观测误差ε的获取由所述的观测器模块中的两个乘法单元和一减法单元实现，其中第一乘法单元将所述的解调模块输出的旋转变压器的旋转角度θ的正弦值sinθ和所述的观测角度的余弦值相乘获取第二乘法单元将解调模块输出的余弦值和所述的观测角度的正弦值相乘获取减法单元使所述的第一乘法单元的输出与第二乘法单元的输出相减，由第一乘法单元的输出值减去第二乘法单元的输出值，获取观测误差(注意，在无限小的情况下，有

所述的角度观测器模块的传递函数为：

其中，ki为积分系数，kp为比例系数，且所述的ki由所述的旋转变压器的固有频率ωn确定，所述的kp由所述的旋转变压器的固有频率ωn以及所述的旋转变压器的阻尼因子ξ确定。

所述的ki与所述的kp分别为：

kp＝2ξωn；

其中，所述的ωn为旋转变压器的固有频率，所述的ξ为所述的旋转变压器的阻尼因子。

在一种具体实施方式中，该系统基于英飞凌aurix系列tc275单片机，片上集成deltasigmaadc模块，取代传统的adc，主要用于旋转变压器的输出的模拟信号的采样和处理，不需要额外的专用芯片或硬件电路，而deltasigmaadc模块单元的具体结构如图2所示。

在使用deltasigmaadc模块单元进行高频精确采样时，是基于deltasigmaadc模块单元的过采样功能进行的高频精确采样，而过采样率osr每增加一倍，信噪比snr可增加3db，即分辨率增加了0.5bit，因此，过采样率osr的大小直接影响了模块采样的有效位数。而在一种具体实施例中，将deltasigmaadc模块单元的模数采样速率配置在10mhz至20mhz之间，通过对模块内不同的滤波器参数进行配置，其内部的滤波和抽取部分使得过采样率osr在4至512之间，从而使采样速率降低至合适的数据结果输出速率。在一个确定的osr条件下，该模块不会产生数据丢失。在输入信号带宽30khz～100khz的条件下，其信噪比可达74～80db，对输入信号采样的有效位数可达12～13位。

旋转变压器的激励信号本身是一个高频的正弦信号，根据旋变的工作原理可知，两个定子绕组中感应出来的正余弦信号包含了此高频信号。虽然旋转变压器输出的模拟信号经过deltasigmaadc模块单元后再经过进一步的抽取滤波后得到高分辨率的数字信号，但此数字信号仍然含有载波信号，为了获得与角度直接相关的正余弦信号，必须使用解调模块把载波信号从该数字信号中解调出来。首先对此数字信号进行反向整形，然后再通过积分运算就可以实现载波信号的解调。

解调的具体过程如图3所示，图3中的①为旋转变压器输出信号经滤波抽取后的信号曲线，其对应着一个360°的轴旋转周期。对该曲线中一个载波周期的信号进行分析，获取②，再通过deltasigmaadc模块单元内部的载波信号正负标志(请参见③)，在0～180°的旋转位置内，将负半轴的信号进行反转(请参见④)，以此类推，将该区间内的波形信号全部反转到了正半轴。同理，对于180°～360°的旋转位置，将正半轴的信号全部反转到负半轴，最终的到的波形效果如⑤所示，从而获得一条完整的360°旋转周期内的调制正弦曲线，再经一系列积分处理，即可得到光滑的正弦曲线，同理可得另一定子绕组中的余弦曲线。

通过以上的信号处理，对于旋转变压器一个固定的旋转位置，均可以通过这两个正余弦信号来进行其角度计算。采用基于锁相环的角度观测器模块进行解算，具有较高的分辨率和抗干扰性，除了可以使角度解算的精确度获得大大的提高以外，系统也获得了更好的鲁棒性。

基于锁相环的角度观测器模块中包含基于数字锁相环的角度观测器闭环跟踪算法，请参阅图4，在一种具体实施例中，可由角度观测器模块获取误差的数学表达式为：

式中为观测器误差，为观测估计角度值，θ为转子实际角度值。若当(观测误差)无限小，则有

图4为典型的基于二阶角度跟踪观测器原理图，是一种基于锁相环的角度观测器模块的具体实施例，在该具体实施例中，闭环系统中积分器和pi控制器的使用使得观测器的输出更平滑，具有很好的角度跟踪性。所述的角度观测器模块将旋转变压器的正弦值和余弦值，以及所述的角度观测器模块获取的观测角度的正弦值与余弦值相比较以后，通过常见的闭环系统就能把系统误差调整到最小化。

拥有更平滑的系统性能也是观测器优于反正切法的重要原因。图4中角度观测器模块的传递函数为：

通过其特征多项式与典型的ⅱ型系统进行系数匹配，根据动态性能确定所需的ωn及ξ，则可以计算角度观测器的系数为：

kp＝2ξωn；

其中ωn为固有频率，ξ为阻尼因子。

请参阅图5，在具体实施例中，采用基于过采样原理的deltasigmaadc对模拟信号进行高频精确采样会产生系统的相位滞后，可在算法中加入延时校正来进行补偿，回路参数条件变化时延时校正补偿可自动调节，一种具体的实施方法为：在所述的观测器模块中，对计算出的相位进行补偿，然后反馈到系统中，形成闭环回路，实现动态调整。对于数字信号中包含的载波信号的解调主要通过反向整形和积分运算实现，解调后的信息再经过最后的观测器算法进行了转子角度信号的实时解算，实现了旋转变压器的低成本、高性能、高集成度的角度变换。

采用本发明的基于dsadc的旋变软件解码系统及其方法，直接利用主mcu中自带的dsadc模块进行软件解码，不需要额外的芯片或者mcu，由于采用基于过采样原理的deltasigmaadc对模拟信号进行高频精确采样会产生系统的相位滞后，在系统中加入延时校正来进行补偿，回路参数条件变化时延时校正补偿可自动调节。对于数字信号中包含的载波信号的解调主要通过反向整形和积分运算实现，解调后的信息再经过最后的观测器模块进行了转子角度信号的实时解算，而相位误差的补偿也由所述的观测器模块实现，具有高精确度和高动静态性能的特点，可以节约硬件开发成本，避免了资源的浪费，从而创造出更好的经济效益，从而实现了旋转变压器的低成本、高性能、高集成度的角度变换，不需要额外的mcu专门进行软件解码，不需要自己单独设计硬件电路对信号进行处理、对信号处理中的滤波等进行补偿、计算转子位置时通过二阶锁相环的结构计算得到转子位置，能够快速准确地得到转子位置，动态响应性能好，抗干扰能力强，稳态时能够消除偏差，明显优于cordic算法。

在此说明书中，本发明已参照其特定的实施例作了描述。但是，很显然仍可以作出各种修改和变换而不背离本实用精神和范围。因此，说明书和附图应被认为是说明性的而非限制性的。