一种基于聚能量字典学习的张量压缩方法与流程

本发明属于信号处理领域，具体涉及基于聚能量字典学习的张量信号压缩算法，可以实现张量信号的有效压缩。

背景技术：

随着信息技术的发展，多维信号在信号处理领域发挥着越来越重要的作用。与此同时多维(multidimensional，md)信号也会给传输和存储过程带来很大的负担。为了应对多维信号处理带来的挑战，多维信号的张量表示引起了人们的关注，将多维信号表示为张量并对其进行处理，为多维信号的处理带来极大的方便。因此，对多维信号的压缩本质上就是对张量进行有效压缩，所以张量压缩算法在多维信号压缩领域发挥着越来越重要的作用，已成为当今研究的热点。

近年来，针对张量压缩的问题，研究者们在cp分解和塔克分解算法的基础上提出了很多有效地压缩算法，大致的分为两个方面，一种是针对张量数据本身，直接在张量分解地基础上对张量数据惊醒矢量化操作。然而，根据著名的“丑小鸭”定理，没有任何先验知识就没有最优的模式表示，换句话说，张量数据的矢量化并不总是有效的。具体来说，这可能会导致以下问题：首先，破坏原始数据中固有的高阶结构和固有相关性，信息丢失或掩盖冗余信息和原始数据的高阶依赖性，因此，不可能在原始数据中获得可能更有意义的模型表示；第二，矢量化操作会生成高维向量，导致出现“过度拟合”，“维度灾难”和小样本问题。

另一方面，张量的稀疏表示被应用到张量的压缩当中。由于张量塔克模型和kronecker表示的等价性，张量可以被定义为具有特定稀疏性的给定kronecker字典的表示形式，例如多向稀疏性和块稀疏性。随着张量稀疏性的出现，一些稀疏编码的方式也随之出现，例如kroneker-omp和n-wayblockomp等算法，这些算法为张量压缩带来了极大的便利；同时，与各种稀疏编码算法相对应的也产生了很多字典学习算法，在各个维度上分别对张量进行稀疏编码和字典学习，从而实现稀疏表示的目的。然而，以上基于稀疏表示的张量处理算法的过程中，往往会引入一些新的噪声，这将对数据的准确性产生一定的影响。并且，在稀疏表示过程中，稀疏度的确定也会给张量的处理带来一定的挑战。

所以，在处理包含大数据量的张量中，在对张量进行有效地压缩，提取出有用信息，降低传输和存储成本方面面临着前所未有的挑战。

技术实现要素：

本发明旨在解决以上现有技术的问题。提出了一种能够提升原始数据保存能力，增强去噪能力的基于聚能量字典学习的张量压缩方法。本发明的技术方案如下：

一种基于聚能量字典学习的张量压缩方法，其包括以下步骤：

步骤1)：获取多维信号并将多维信号表示为张量，输入张量并进行稀疏表示和塔克分解；

步骤2)利用稀疏表示中稀疏系数张量与塔克分解得到的核心张量的近似关系，得到关于原始张量的新的张量稀疏表示形式；；

步骤3)对步骤2)新的张量稀疏表示形式，根据张量运算性质，转换为关于字典表示的映射矩阵形式；

步骤4)利用聚能量字典学习算法降维的思想对映射矩阵中的字典进行降维，从而实现张量的压缩。

进一步的，所述步骤1)通过塔克分解得到核心张量在每个维度上与映射矩阵乘积的形式，在塔克分解过程中，得到如下表示

a∈r^i×p,b∈r^j×q,c∈r^k×r,为正交矩阵又称为因子矩阵，反应了各个维度上的主成分，z∈r^p×q×r为核心张量，反应了各个维度的相关情况，p、q和r分别对应因子矩阵a、b和c的列数，i、j和k表示原始张量每个维度的大小，若p、q、r小于i、j、k，那么核心张量可以看做是原始张量的压缩；

对于n阶张量，塔克分解形式为

χ＝z×1a1×2a2...×nan

χ表示输入的张量信号，z表示核心张量，ai表示各个维度上的分解矩阵，为正交矩阵。

进一步的，所述步骤1)张量的稀疏表示的表示形式为

表示稀疏表示之后的信号，s表示稀疏系数张量，n表示自张量的阶数，di表示各个维度上的字典。

进一步的，所述步骤2)通过观察张量的稀疏表示和塔克分解形式，发现两个表达式是相似的，由塔克分解得到核张量的表示为

z＝χ×1a1^t×2a2^t...×nan^t

利用稀疏系数张量和核张量的近似关系，将核张量的表达式代入张量稀疏表示中得到

进一步的，所述步骤3)对步骤2)新的张量稀疏表示形式，根据张量运算性质，转换为关于字典表示的映射矩阵形式，具体包括：

在张量的运算中，

当m≠n时，

ψ×ma×nb＝ψ×n(ba)

其中ψ表示n阶张量，×m表示张量与矩阵的m模乘积，×n表示张量与矩阵的n模乘积。

当m≠n时，

ψ×ma×nb＝ψ×nb×ma

将以上的两个性质应用到新的稀疏表示中，可以得到

进一步的，所述步骤4)利用聚能能量字典学习算法降维的思想对映射矩阵中的字典进行降维，从而实现张量的压缩，具体步骤包括：

输入：t个训练样本构成的张量稀疏度k，最大迭代次数itermax，终止门限ε

1.初始化字典为高斯矩阵，并对各个字典的列进行归一化

2.塔克分解：χ＝z×1a1×2a2...×nan；

3.初始化字典经过聚能量字典学习算法中的γ(d)过程；

4.计算更新次数i＝0时s，并利用计算未经任何迭代更新时的绝对误差e0；

5.第i次字典更新

fork＝1:in

利用计算第i个字典的更新值

end

6.对上一步中求得的n个字典进行归一化；

7.利用第i次更新的字典，更新稀疏系数张量si；

8.计算第i次更新后的绝对误差ei和相对误差er；

9.终止条件判断，若er＜ε或者迭代次数超出最大限制，则终止循环，否则继续步骤5-8；

10.得到字典

11.根据式得到ud，则字典

12.将字典p带入

输出：压缩张量

进一步的，为了使降维之后的字典p保留原始字典d中的主成分，需要对字典d进行预处理，处理过程如下

d^td＝uλv^t

u为奇异值分解的左奇异矩阵，v为右奇异矩阵，λ为奇异值矩阵，表示形式为其次对奇异值进行更新

其中，k表示字典列数，td表示主成分阈值，表示更新后的前d个奇异值，表示更新后的后r个奇异值。

从而得到新的奇异值

与初始左奇异矩阵和右奇异矩阵构成新的字典，即

进一步的，在对字典进行预处理之后，需对字典进行更新，在更新过程中采用基于张量的多维字典学习算法tksvd，完成对高维张量信号的字典更新过程，与k-svd字典更新算法不同的是，tksvd算法中，具体包括：

(1)在进行张量字典学习时，与二维信号学习方式不同，根据张量范数的定义，可得到：

其中，dn第n维字典，d1表示第1维字典，it表示t阶单位阵，通过最小二乘法求解上式，得到字典di的更新值为

其中，yi表示张量的i模展开矩阵，表示伪逆，即其中表示矩阵m的伪逆矩阵，m^t表示矩阵m的转置矩阵。另一方面，完成一次迭代后，计算在当前字典和稀疏系数下可以恢复的数据与原始的训练数据之间的绝对误差和相对误差，第i次迭代后的绝对误差仍以张量的frobenius范数定义

其中s表示系数张量、表示移除g个原子后真实信号与逼近信号的误差。

对字典进行更新完成之后，对字典进行降维处理，对更新后的字典进行奇异值分解

其中ud表示左奇异矩阵的前d列，ur表示左奇异矩阵的后r列，θd表示奇异值矩阵的前d个奇异值，θr表示奇异值矩阵的后r个奇异值，vd表示右奇异矩阵的前d列，vr表示右奇异矩阵的后r列。则降维后的字典表示为将降维后的字典p代入映射矩阵t中，从而完成张量压缩。

本发明的优点及有益效果如下：

本发明提出一种基于聚能量字典学习的张量压缩算法。具体创新步骤包括：1)将张量的稀疏表示应用到张量压缩中，在去噪能力方面优于其他算法；2)通过对映射矩阵的降维完成张量的压缩，避免了矢量化操作对张量内部数据结构的破坏；3)对张量的字典采用聚能能量字典学习算法降维，使得每一维度上的数据之间的数据结构能够得以保留，提高了数据保留能力。

附图说明

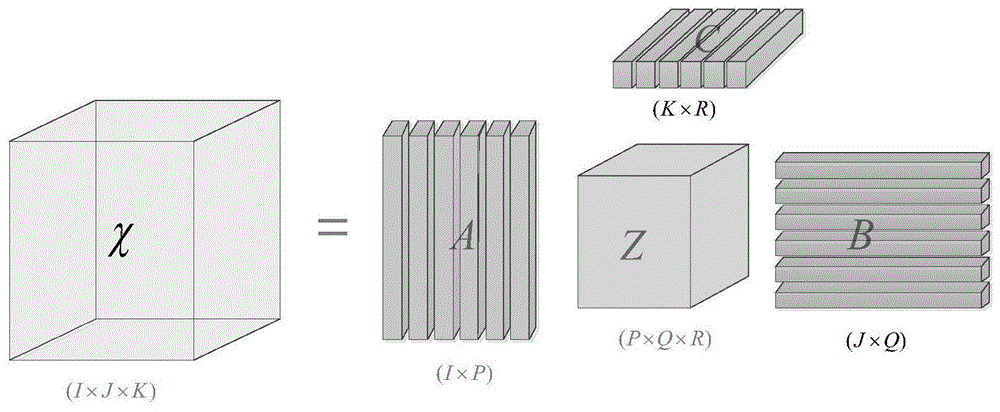
图1是本发明提供优选实施例中所用到的三阶张量塔克分解图；

图2是基于聚能量字典学习的张量压缩算法示意图；

图3是基于聚能量字典学习的张量压缩算法流程图。

具体实施方式

下面将结合本发明实施例中的附图，对本发明实施例中的技术方案进行清楚、详细地描述。所描述的实施例仅仅是本发明的一部分实施例。

本发明解决上述技术问题的技术方案是：

本发明重点解决在传统张量压缩算法中，破坏数据结构，导致信息丢失以及引入新的噪声的问题。主要思路是通过塔克分解和稀疏表示得到字典、稀疏系数张量和核张量，然后通过稀疏系数张量与核张量的近似关系构成新的稀疏表示形式，最后利用聚能量字典学习算法对稀疏表示中的字典进行降维，从而实现张量的压缩。

图2为本发明的总体流程图，下面结合附图进行说明，包括以下几个步骤：

步骤一：对输入张量同时进行稀疏表示和塔克分解，在稀疏表示过程中，得到如下表示

张量经稀疏表示之后，得到稀疏系数张量在每个维度上乘积的形式，换句话说，稀疏表示中，稀疏系数张量以字典d作为映射矩阵，在每个维度上进行投影，从而得到稀疏化后的张量。

给定一个三阶张量χ∈r^i×j×k，其塔克分解过程如图1所示。在塔克分解过程中，得到如下表示

a∈r^i×p,b∈r^j×q,c∈r^k×r,为正交矩阵又称为因子矩阵，反应了各个维度上的主成分，z∈r^p×q×r为核心张量，反应了各个维度的相关情况。p、q和r分别对应因子矩阵a、b和c的列数，i、j和k表示原始张量每个维度的大小，若p、q、r小于i、j、k，那么核心张量可以看做是原始张量的压缩。

更一般地，对于n阶张量，塔克分解形式为

χ＝z×1a1×2a2...×nan

步骤二)利用稀疏表示中稀疏系数张量与塔克分解得到的核心张量的近似关系，得到关于原始张量的新的张量稀疏表示形式。

通过观察张量的稀疏表示和塔克分解形式，发现两个表达式是相似的，由塔克分解得到核张量的表示为

z＝χ×1a1^t×2a2^t...×nan^t

利用稀疏系数张量和核张量的近似关系，将核张量的表达式代入张量稀疏表示中得到

步骤三：对新的张量稀疏表示形式，根据张量运算性质，转换为关于字典表示的映射矩阵形式，具体步骤包括：

在张量的运算当中，当m≠n时，

ψ×ma×nb＝ψ×n(ba)

其中ψ表示n阶张量，×m表示张量与矩阵的m模乘积，×n表示张量与矩阵的n模乘积。

当m≠n时，

ψ×ma×nb＝ψ×nb×ma

将以上的两个性质应用到新的稀疏表示中，可以得到

令ti＝diai^t，将ti带入上式，得到

从上式看出，稀疏表示为一个关于原始矩阵在个维度上投影的形式。在mpca算法中，高维张量通过投影矩阵的处理实现张量压缩，即，通过保留投影矩阵的主成分，达到投影矩阵压缩的目的，从而实现张量压缩。收到mpca思想的启发，这里对矩阵ti进行降维，从而实现原始张量χ的压缩。为完成对矩阵ti的降维，这里对考虑稀疏ti的字典d进行降维，从而实现对映射矩阵ti的降维。

步骤四：利用聚能能量字典学习算法中字典降维的思想实现对张量的压缩。算法中为使降维之后的字典p保留原始字典d中的主成分，需要对字典d进行预处理，处理过程如下

d^td＝uλv^t

u为奇异值分解的左奇异矩阵，v为右奇异矩阵，λ为奇异值矩阵，表示形式为其次对奇异值进行更新

其中，k表示字典列数，td表示主成分阈值，表示更新后的前d个奇异值，表示更新后的后r个奇异值。

从而得到新的奇异值

与初始左奇异矩阵和右奇异矩阵构成新的字典，即

在对字典进行预处理之后，需对字典进行更新，在更新过程中采用基于张量的多维字典学习算法(tksvd)，完成对高维张量信号的字典更新过程。与k-svd字典更新算法不同的是，tksvd算法中，需要注意的有两点：

(2)在进行张量字典学习时，与二维信号学习方式不同，根据张量范数的定义，可得到：

其中，it表示t阶单位阵，dn第n维字典，d1表示第1维字典。显然可以通过最小二乘法求解上式，可以得到字典di的更新值为

其中，yi表示张量的i模展开矩阵，表示伪逆，即其中表示矩阵m的伪逆矩阵，m^t表示矩阵m的转置矩阵。另一方面，完成一次迭代后，可以计算在当前字典和稀疏系数下可以恢复的数据与原始的训练数据之间的绝对误差和相对误差，第i次迭代后的绝对误差仍以张量的frobenius范数定义

其中s表示系数张量、表示移除g个原子后真实信号与逼近信号的误差。

对字典进行更新完成之后，对字典进行降维处理。对更新后的字典进行奇异值分解

其中ud表示左奇异矩阵的前d列，ur表示左奇异矩阵的后r列，θd表示奇异值矩阵的前d个奇异值，θr表示奇异值矩阵的后r个奇异值，vd表示右奇异矩阵的前d列，vr表示右奇异矩阵的后r列。则降维后的字典表示为将降维后的字典p代入映射矩阵t中，从而完成张量压缩。

为基于聚能量字典学习的张量压缩算法，具体的步骤包括：

输入：t个训练样本构成的张量稀疏度k，最大迭代次数itermax，终止门限ε

1.初始化字典为高斯矩阵，并对各个字典的列进行归一化

2.塔克分解：χ＝z×1a1×2a2...×nan

3.初始化字典经过聚能能量字典学习算法中的γ(d)过程

4.计算更新次数i＝0时s，并利用计算未经任何迭代更新时的绝对误差e0

5.第i次字典更新

fork＝1:in

利用计算第i个字典的更新值

end

6.对上一步中求得的n个字典进行归一化

7.利用第i次更新的字典，更新稀疏系数张量si

8.计算第i次更新后的绝对误差ei和相对误差er

9.终止条件判断，若er＜ε或者迭代次数超出最大限制，则终止循环，否则继续步骤5-8

10.得到字典

11.根据式得到ud，则字典

12.将字典p带入

输出：压缩张量

以上这些实施例应理解为仅用于说明本发明而不用于限制本发明的保护范围。在阅读了本发明的记载的内容之后，技术人员可以对本发明作各种改动或修改，这些等效变化和修饰同样落入本发明权利要求所限定的范围。