基于全通滤波器的两通道IIR的QMF组设计方法与流程

本发明属于数字信号处理技术领域，具体涉及一种改进的基于全通滤波器的两通道iir正交镜像滤波器组设计方法。

背景技术：

在过去的几十年里，数字信号处理系统已经陆续取代了模拟系统，今天，在各种不同的设备上都可以找到数字信号处理系统的身影，如移动通信系统、消费者电子产品和汽车电子产品，或者助听器。数字信号处理的一个决定性的优势是一个系统可以通过数字信号处理来实现，而不能或几乎不能通过模拟处理来实现。许多数字信号处理算法的一个重要组成部分是滤波器及其作为滤波器组的串联。滤波器组主要用于信号的频谱分析，作为跨多路复用器，或处理子带频域或时域信号。最后提到的处理子带信号需要一个分析-合成滤波器组来获得重建的时域信号。本发明研究的就是正交镜像滤波器组(qmfb，quadraturemirrorfilterbank)。

近年来两通道qmfb被应用于越来越多的领域，例如语音和图像信号的子带编码，小波基设计等。由于qmfb的广泛应用，人们对于它的设计关注也越来越重视。

x.zhang和h.iwakura提出了一种利用数字全通滤波器(dafs，digitalallpassfilters)设计qmfb的方法。由全通滤波器和纯延迟部分组成的qmfb具有近似线性的相位响应，使用另一个附加的dafs作为均衡器可以使相位畸变最小化。论文中采用一个dafs和一个纯延迟共同设计一个qmfb，设计dafs的方法是其于1992年提出的一个算法，简单可以描述为一种基于特征值问题设计等纹波相位响应的dafs的新方法，并通过计算最大特征向量和迭代法得到了最优滤波系数。这种算法借用等波纹设计fir的方法得到了全通滤波器，但是其计算极其复杂，并且该算法并没有考虑全通滤波器和纯延迟合成时的相位误差和得到的低通滤波器的阻带误差。

s.s.lawson和a.klouche-djedid提出了另外一种利用dafs设计qmfb的方法，该方法具体表现为把全通滤波器的相位分解为分子和分母两部分，并只对分子部分进行优化，所采用的优化方法是根据正弦函数和余弦函数的正交性质，进行近似积分，从而得到全通滤波器的系数。

技术实现要素：

本发明针对现有技术的不足，提出了一种基于全通滤波器的两通道iir的qmf组设计方法。

本发明一种改进的基于全通滤波器的两通道iir正交镜像滤波器组设计方法。该方法具体包括以下步骤：

步骤一、根据设计要求，确定全频带上的频率点数l、两个全通滤波器的阶数n1和n2、分析滤波器中的低通滤波器的通带截止频率ωp，阻带截止频率ωs，令迭代初始系数k＝0，第k次的全通滤波器系数ai(k)＝0，初始加权值wi＝1，i＝1,2；其中n1＝n2+1；

步骤二、确定全通滤波器的实际相位误差。

2.1.确定全通滤波器的理想相位

全通滤波器的理想相位在ω∈[0,π]的频率带上满足：当iir滤波器的相位满足ω＝0时，相位是0；当ω＝π时，相位满足θ(π)＝-nπ；此时全通滤波器是稳定的；全通滤波器的理想相位分别是θd1＝-n1ω+0.25ω和θd2＝-n2ω+0.25ω。

2.2.求全通滤波器的实际相位误差

通过(1)、(2)、(3)式分别得到全通滤波器ai(e^jω)的表达式、实际相位表达式和实际相位误差，其中ω∈[0,2ωp]，i＝1,2。

θei(ω)＝θi(ω)-θdi(ω)(3)

其中ai(n)表示滤波器系数ai的第n个元素，n＝1,2,…,ni；

步骤三、求解得出第k次迭代下全通滤波器的滤波器系数ai(k)。

3.1.得到目标优化函数表示为

其中φ(ai(k-1),ω)表示第k-1次迭代的φ(ω)

ψ(ω)＝niω+θdi(ω)(6)

该目标函数是最大最小化问题，同时也是一个高度非线性的问题，步骤3-2可将该非线性问题转换为线性问题；

3.2.计算第k-1次迭代所得的φ(ai(k-1),ω)关于系数ai(k-1)的一阶偏导数如式(7)所示。

3.3.计算第k次迭代时全通滤波器ai(e^jω)的相位误差θei(ω)如式(8)所示。

式(8)中，δi代表第k次迭代时全通滤波器ai(e^jω)的系数增量，δi＝ai(k)-ai(k-1)。

3.4.第k次迭代时优化目标函数表示为凸优化问题进行求解，确定第k次迭代的系数增量δi

步骤四、若式(10)不成立，则转到步骤五。若式(10)成立，则将ai(k)作为最终设计出的全通滤波器ai(e^jω)的系数，迭代结束。

式(10)中，是第k次迭代中确定的全通滤波器ai(e^jω)的群延迟误差。是第k-1次迭代中确定的全通滤波器ai(e^jω)的群延迟误差。μ是设定的阈值。

步骤五、根据群延迟误差的包络计算加权值wi

首先计算出第k次迭代的群延迟误差其中gdi表示第k次迭代的全通滤波器ai(e^jω)的实际群延迟，τdi表示全通滤波器ai(e^jω)的理想群延迟；然后计算出的包络如果不满足则使然后令返回步骤三；否则的话直接令返回步骤三。其中ε为设定的阈值。

本发明具有的有益效果是：

本发明主要针对每个全通滤波器的相位进行优化，保证了信号经过的每一个子滤波器都具有更近似线性的相位，减少相位失真的可能性，达到设计预期目标。本发明与其他方法相比，最大的改进就在于分开确定每个全通滤波器的系数，不再联合设计，使得到的系数更加精准，不再互相影响，保证了设计的一定自由度；同时确保了信号在任何时间段都没有相位失真从而达到重构并且在有限的迭代次数中可以得到更好的性能指标。

附图说明

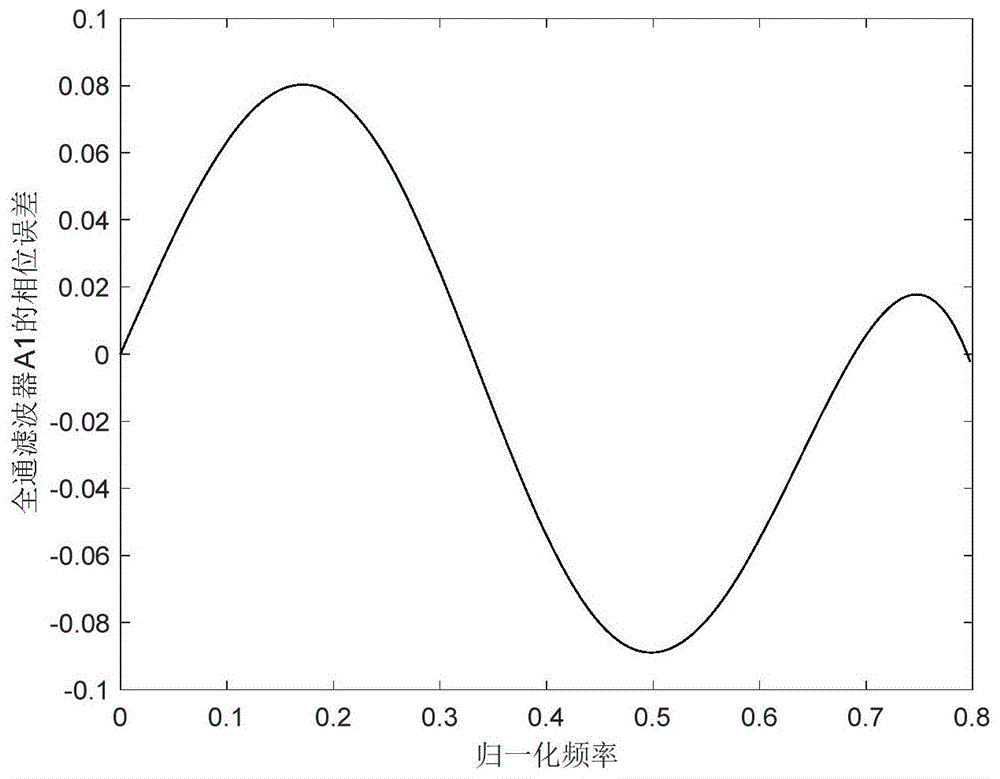
图1为表1中的系数所画出的全通滤波器a1的相位误差。

图2为表1中的系数所画出的全通滤波器a2的相位误差。

图3为表1中的系数所画出的qmfb幅频响应图。

图4为表1中的系数所画出的qmfb重构误差频率响应图。

图5为表1中的系数所画出的重构滤波器的相位误差。

具体实施方式

以下结合附图对本发明作进一步说明。

改进的基于全通滤波器的两通道iir正交镜像滤波器组设计方法的具体步骤如下：

步骤一、根据设计要求，确定全频带上的频率点数l、两个全通滤波器的阶数n1和n2、分析滤波器中的低通滤波器的通带截止频率ωp，阻带截止频率ωs，令迭代初始系数k＝0，第k次的全通滤波器系数ai(k)＝0，初始加权值wi＝1，i＝1,2；其中n1＝n2+1；

步骤二、确定全通滤波器的实际相位误差。

2.1.确定全通滤波器的理想相位

全通滤波器的理想相位在ω∈[0,π]的频率带上满足：当iir滤波器的相位满足ω＝0时，相位是0；当ω＝π时，相位满足θ(π)＝-nπ；此时全通滤波器是稳定的；全通滤波器的理想相位分别是θd1＝-n1ω+0.25ω和θd2＝-n2ω+0.25ω。

2.2.求全通滤波器的实际相位误差

通过(1)、(2)、(3)式分别得到全通滤波器ai(e^jω)的表达式、实际相位表达式和实际相位误差，其中ω∈[0,2ωp]，i＝1,2。

θei(ω)＝θi(ω)-θdi(ω)(3)

其中ai(n)表示滤波器系数ai的第n个元素，n＝1,2,…,ni；

步骤三、求解得出第k次迭代下全通滤波器的滤波器系数ai(k)。

3.1.得到目标优化函数表示为

其中φ(ai(k-1),ω)表示第k-1次迭代的φ(ω)

ψ(ω)＝niω+θdi(ω)(6)

该目标函数是最大最小化问题，同时也是一个高度非线性的问题，步骤3-2可将该非线性问题转换为线性问题；

3.2.计算第k-1次迭代所得的φ(ai(k-1),ω)关于系数ai(k-1)的一阶偏导数如式(7)所示。

3.3.计算第k次迭代时全通滤波器ai(e^jω)的相位误差θei(ω)如式(8)所示。

式(8)中，δi代表第k次迭代时全通滤波器ai(e^jω)的系数增量，δi＝ai(k)-ai(k-1)。

3.4.第k次迭代时优化目标函数表示为凸优化问题进行求解，确定第k次迭代的系数增量δi

步骤四、若式(10)不成立，则转到步骤五。若式(10)成立，则将ai(k)作为最终设计出的全通滤波器ai(e^jω)的系数，迭代结束。

式(10)中，是第k次迭代中确定的全通滤波器ai(e^jω)的群延迟误差。是第k-1次迭代中确定的全通滤波器ai(e^jω)的群延迟误差。μ是一个极小的实数，可根据设计要求确定。

步骤五、根据群延迟误差的包络计算加权值wi

首先计算出第k次迭代的群延迟误差其中gdi表示第k次迭代的全通滤波器ai(e^jω)的实际群延迟，τdi表示全通滤波器ai(e^jω)的理想群延迟；然后计算出的包络如果不满足则使然后令返回步骤三；否则的话直接令返回步骤三。其中ε是一个极小的实数，可根据设计要求设定。

为了本发明的有效性，对本发明进行了计算机模拟仿真。

模拟仿真中的设计要求：全通滤波器阶数n1＝3，n2＝2，全频带上的频率点数l为8n1+1，通带截至频率ωp＝0.4π，阻带截止频率ωs＝0.6π，最小化重构误差，最大化阻带衰减。

用本发明设计，两个全通滤波器都经过5次迭代，得出最终滤波器的滤波器系数，如表1所示，表1中的系数所画出的全通滤波器a1的相位误差如图1所示，表1中的系数所画出的全通滤波器a2的相位误差如图2所示；其对应的qmfb幅频响应、重构误差频率响应和相位误差响应如图3、图4和图5所示。

表1本发明设计的qmfb中全通滤波器a1和a2的系数表

最后用得出的滤波器系数，计算出低通分析滤波器的最大阻带衰减(psr)，qmfb重构响应的最大相位误差(mvpr)，最大群延迟误差(mvgr)，以及重构响应误差(mvfbr)。

计算公式如下：

其中，h0(e^jω)为所得低通分析滤波器的幅度响应；gd为qmfb的理想群延迟；t(e^jω)为整体失真传输函数。计算得出的指标如表2所示。

表2本发明与lawson和djedid方法关键指标比较

从表2可以看出，本发明所获得的qmfb在上述各项关键指标上都要优于lawson和djedid计方法。