一种自适应巴特沃斯低通数字滤波器设计方法与流程

本发明属于飞机变频交流供电系统抗混叠滤波技术领域，具体为一种适用于变频交流供电系统的自适应巴特沃斯低通数字滤波器设计方法。

背景技术：

飞机供电系统中通常包含大功率二极管整流电路、雷达等非线性负荷，对系统交流电压和电流造成谐波污染。此外，高强度辐射场等高频干扰也会作用于控制电路，对系统的稳定运行构成极大的威胁。采用抗混叠滤波器是有效抑制谐波和高频干扰对系统不利影响的重要手段。

三相变频交流供电系统具有频率变化速度快(国标中规定的最大频率变化率为250hz/s)和频率变化范围大(目前使用的宽变频供电系统的正常频率范围为360hz-800hz)等特点，给抗混叠滤波器的设计带来了巨大的挑战。按照固定的截止频率设计滤波器参数，在实际频率增大时会导致相位滞后增加，降低系统的稳定裕度；当系统运行于低频阶段时，相当于增大滤波器的截止频率，会降低滤波的效果，对系统的性能和稳定性造成不利影响。

现有的滤波器多采用无源器件实现，其通频带内的增益不平稳且过度频带过宽，滤波效果不佳；电力系统中虽然已有成熟的基于运算放大器的有源低通滤波电路，但是相应的结构仅适用于频率固定或在很小范围变化的应用。另一种方法是对频率范围进行分段，针对每一段设计一个固定截止频率的滤波器。这种方法一方面增加了硬件的复杂程度和成本，同时还容易造成在不同截止频率滤波器间切换时输出不连续的现象，影响系统的性能和稳定性。

技术实现要素：

为解决现有技术存在的问题，本发明针对变频交流供电系统提出一种截止频率随被测信号基波频率连续调整的自适应巴特沃斯低通数字滤波器设计方法，用于对变频交流电压、电流信号进行抗混叠滤波，提高对电压、电流基频信号检测的精确度，从而提高变频交流供电系统的电压精度，增强供电系统的稳定性。

本发明的技术方案为：

所述一种自适应巴特沃斯低通数字滤波器设计方法，其特征在于：包括以下步骤：

步骤1：将m阶巴特沃斯低通滤波器的归一化传递函数表达为复频域的传递函数；

步骤2：将步骤1得到的m阶巴特沃斯低通滤波器复频域传递函数离散化，并表达为采样频率ts和截止频率wc乘积的函数为：

其中nm、nm-1…n1、n0和dm、dm-1…d1、d0分别是ha(z)中分子和分母多项式的系数，均为采样频率ts和截止频率wc乘积的函数；

步骤3：将ha(z)中分母多项式化为首1的形式，得到新的分子、分母多项式系数nmn、n(m-1)n…n1n、n0n和dmn、d(m-1)n…d1n、d0n，其中dmn＝1；

新的分子、分母多项式系数分别表达为：

nkn＝fkn(a0,a1…am),k＝0,1,…m

dkn＝fkd(a0,a1…am),k＝0,1,…m

a0＝tswc，a2…am为以a0为参数的多项式，fkn()和fkd()也为多项式函数；

步骤4：获取被检测信号的采样频率ts和基波频率ws，将巴特沃斯低通滤波器的截止频率wc取为取被检测信号基波频率ws的比例关系：wc＝kws，其中k为设定常数；

步骤5：根据分子、分母多项式系数表达式

nkn＝fkn(a0,a1…am),k＝0,1,…m

dkn＝fkd(a0,a1…am),k＝0,1,…m

以及步骤4中得到的被检测信号的采样频率ts和巴特沃斯低通滤波器的截止频率wc，得到巴特沃斯低通滤波器传递函数分子、分母多项式系数nkn、dkn，从而根据被检测信号更新巴特沃斯低通滤波器传递函数，然后对输入信号采用更新后的巴特沃斯低通滤波器进行滤波输出。

进一步的，所述自适应巴特沃斯低通数字滤波器采用c语言在fpga中编程实现。

进一步的，所设计自适应巴特沃斯低通数字滤波器为3阶自适应巴特沃斯低通数字滤波器，其中步骤2中，离散化后的传递函数分子分母系数为：

步骤3中，

a0＝tswc，a3＝a2+4a1+8a0+8

得到新的分子、分母多项式系数为

n0n＝a2/a3n1n＝3n0n2n＝3n0n3n＝n0

d0n＝(a2-4a1+8a0-8)/a3

d1n＝(3a2-4a1-8a0+24)/a3

d2n＝(3a2+4a1-8a0-24)/a3

步骤4中，保持滤波器的截止频率为12倍的基波频率wc＝12ws。

有益效果

本发明提出的自适应巴特沃斯低通数字滤波器能够有效减小谐波和高频干扰对变频交流电压、电流信号的影响，提高信号检测的精确度；同时，保证被检测信号的频率在大范围内快速变化时滤波器输出基波频率信号的增益和相移相同，一方面能够简化变频供电系统中交流电压、电流检测电路的设计，另一方面可以增强变频交流供电系统的稳定性。

本发明的附加方面和优点将在下面的描述中部分给出，部分将从下面的描述中变得明显，或通过本发明的实践了解到。

附图说明

本发明的上述和/或附加的方面和优点从结合下面附图对实施例的描述中将变得明显和容易理解，其中：

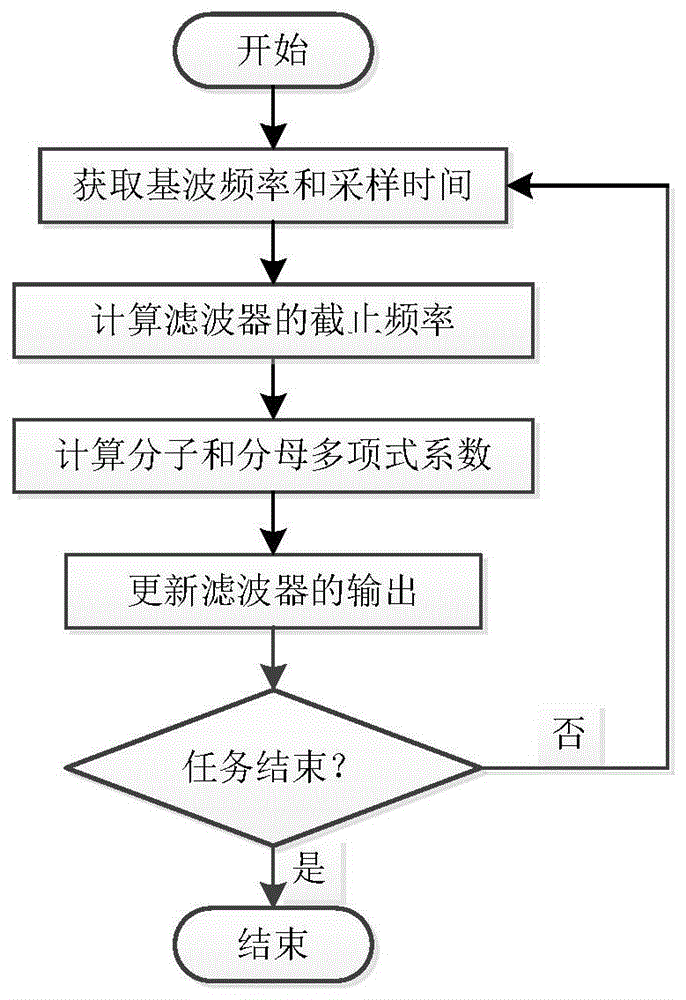
图1是自适应巴特沃斯低通数字滤波器的运算过程。

图2-图5是应用本发明设计的自适应三阶巴特沃斯低通数字滤波器对受到谐波污染的变频交流电压信号进行滤波的结果。其中，电压信号采用标幺值，其基波分量的幅值为1.0，在基波电压上叠加了11和13次谐波，其幅值分别为基波分量的3％和2％，基波频率分别在355hz-365hz和797hz-803hz之间变化，频率的变化率分别为400hz/s和-400hz/s。

图2是频率从355hz以400hz/s上升到365hz的滤波效果。

图3是频率从365hz以-400hz/s下降到355hz的滤波效果。

图4是频率从797hz以400hz/s上升到803hz的滤波效果。

图5是频率从803hz以-400hz/s下降到797hz的滤波效果。

具体实施方式

本发明提出一种截止频率随被检测信号的基波频率连续调整的自适应巴特沃斯低通数字滤波器设计方法，用于对变频交流供电系统中的交流电压、电流信号进行抗混叠滤波，其方法基本原理是：

(1)将离散化的(z域)巴特沃斯低通滤波器传递函数的分子、分母多项式的系数表达为采样步长ts和截止频率wc乘积的函数。

假设离散化后巴特沃斯低通滤波器的传递函数为：

其中，nm、nm-1…n1、n0和dm、dm-1…d1、d0分别是ha(z)中分子和分母多项式的系数，都是tswc及其2到m次方的函数。

(2)将ha(z)中分母多项式化为首1的形式，得到新的分子、分母多项式系数nmn、n(m-1)n…n1n、n0n和dmn、d(m-1)n…d1n、d0n，其中dmn＝1。

其中新的分子、分母多项式系数可分别表达为：

nkn＝fkn(a0,a1…am),k＝0,1,…m

dkn＝fkd(a0,a1…am),k＝0,1,…m

a0＝tswc，a2…am为以a0为参数的多项式，fkn()和fkd()也为多项式函数；

(3)设计巴特沃斯低通滤波器的截止频率wc与被检测信号的基波频率成固定的比例关系，即：

wc＝kws

其中，k是一个设定的常数，ws表示被检测信号的基波频率。

(4)根据a0,a1…am和wc的值计算分子和分母多项式系数nkn、dkn，并更新巴特沃斯低通滤波器传递函数，然后对输入信号采用更新后的巴特沃斯低通滤波器进行滤波输出。

该巴特沃斯低通滤波器可采用c语言在fpga中编程实现数字滤波器，该自适应巴特沃斯低通数字滤波器的运算过程如附图1所示。理论上讲，本发明适用于任何阶次的巴特沃斯滤波器。但是，高阶滤波器的实现复杂并且相位滞后随着阶次的增加而增大，对系统的稳定性不利，实际中以二阶、三阶等低阶滤波器应用最为广泛。下面以三阶巴特沃斯低通数字滤波器为例对本发明提出的设计方法进行说明，所述实施例是示例性的，旨在用于解释本发明，而不能理解为对本发明的限制。

步骤一：将三阶巴特沃斯低通滤波器的归一化传递函数表达为复频域(s域)的传递函数。

三阶巴特沃斯低通滤波器归一化传递函数为：

其中p表示归一化频率。

将p＝s/ωc代入式(1)，可得三阶巴特沃斯低通滤波器的s域传递函数为：

其中，wc表示滤波器的截止频率。

步骤二：将三阶巴特沃斯低通滤波器的传递函数离散化，并表达为采样频率ts和截止频率wc乘积的函数。

将式(2)离散化可得：

其中：

步骤三：将分母多项式化为首1的形式，得到新的分子、分母多项式系数n3n、n2n、n1n、n0n和d3n、d2n、d1n、d0n等。

令：

a0＝tswc，a3＝a2+4a1+8a0+8，

可得：

n0n＝a2/a3(12)

n1n＝3n0(13)

n2n＝3n0(14)

n3n＝n0(15)

d0n＝(a2-4a1+8a0-8)/a3(16)

d1n＝(3a2-4a1-8a0+24)/a3(17)

d2n＝(3a2+4a1-8a0-24)/a3(18)

步骤四：设计巴特沃斯低通滤波器的截止频率wc与被检测信号的基波频率之间的关系为：

wc＝12ws(19)

即保持滤波器的截止频率为12倍的基波频率。

步骤五：根据a0,a1,a2,a3和式(12)到式(19)计算n0n、n1n、n2n、n3n和d0n、d1n、d2n、d3n的值，从而更新巴特沃斯低通滤波器传递函数，然后在上一步的输出结果和系统状态的基础上对输入信号采用更新后的巴特沃斯低通滤波器进行滤波输出。

尽管上面已经示出和描述了本发明的实施例，可以理解的是，上述实施例是示例性的，不能理解为对本发明的限制，本领域的普通技术人员在不脱离本发明的原理和宗旨的情况下在本发明的范围内可以对上述实施例进行变化、修改、替换和变型。