一种基于Gibbs采样器的自适应平滑方法与流程

一种基于gibbs采样器的自适应平滑方法
技术领域
1.本发明属于状态估计技术领域，特别涉及一种自适应平滑方法。


背景技术：

2.rauch-tung-striebel(rts)平滑器，又称为kalman平滑器，被广泛应用于线性状态估计领域。但kalman平滑器仅仅在状态空间模型的过程噪声及观测噪声为高斯分布且噪声统计参数完全已知时才能保证其最优性。模型的噪声参数设置不准确会恶化估计器的性能，甚至可能会导致估计器发散。而在实际的应用中，状态空间模型的噪声统计参数通常难以准确获得，例如基于测距的水下导航系统、gnss/ins组合导航系统等。在这种情况下，kalman平滑器的性能会受到很大的影响。现有的一些自适应估计器可以在一定程度上解决模型噪声参数未知的问题。目前主要的自适应估计方法包括极大似然法、相关方法、方差匹配法及贝叶斯方法。其中贝叶斯方法是其中最为常用的方法，而在贝叶斯方法当中，变分贝叶斯(variational bayes，vb)近似是其中最为常用的工具。但目前基于vb近似的自适应估计方法通常需要进行联合概率密度的自由因子化近似，得到的只是目标概率密度分布的近似解，其准确性通常难以保证。马尔科夫链蒙特卡洛(markov chain monte carlo，mcmc)方法是一种随机近似方法，被广泛应用于贝叶斯推论当中。mcmc可以通过产生一条以目标分布为准静态分布的马尔科夫链来实现对复杂分布的采样。当采样数量足够大时，mcmc方法可以保证产生足够精确的估计。将mcmc方法用于自适应估计领域有潜力得到比基于vb近似的方法更好的估计精度，而目前还未出现相关的研究。由于其简单易用，gibbs采样器是mcmc框架中应用最为广泛的方法。


技术实现要素：

3.本发明的目的是：针对于实际线性状态估计应用中经常出现的线性模型过程噪声方差矩阵以及观测噪声方差矩阵未知的问题，提出一种基于gibbs采样器的自适应平滑方法，可以实现对系统状态以及模型噪声方差矩阵的同时估计。
4.本发明的技术方案是：首先将线性状态空间模型中的过程噪声方差矩阵及观测噪声方差矩阵看作未知的随机变量，将其先验分布建模为逆wishart分布。在gibbs采样器的框架下，将未知的方差矩阵与系统状态同时进行迭代采样。每一个迭代周期的流程为：1)以上一个迭代周期采样出来的过程噪声方差矩阵及观测噪声方差矩阵为条件，基于kalman平滑器计算当前迭代周期的状态后验分布，并从后验分布中采样当前迭代周期的系统状态；2)以当前迭代周期采样出来的系统状态以及观测变量为条件，计算观测噪声方差矩阵的后验分布，并从后验分布当中采样当前迭代周期的观测噪声方差矩阵；3)以当前迭代周期采样出来的系统状态为条件，计算过程噪声方差矩阵的后验分布，并从后验分布中采样当前迭代周期的过程噪声方差矩阵。在进行多次迭代之后，选取达到稳态之后的迭代周期采样的平均值作为最终的状态估计值以及噪声方差矩阵估计值。
5.本发明包括以下步骤：
6.a.将线性状态空间模型中的过程噪声方差矩阵及观测噪声方差矩阵看作随机变量，分别将其先验分布建模为逆wishart分布。
7.b.在gibbs采样器框架下，对线性状态空间模型的过程噪声方差矩阵及观测噪声方差矩阵进行初始采样。
8.c.设置总迭代周期数n以及平稳周期数n
b
，要求满足n
b
＜n；进行n次迭代，每一次迭代周期的流程为：
9.c1.以上一个迭代周期采样出来的过程噪声方差矩阵及观测噪声方差矩阵为条件，基于kalman平滑器计算当前迭代周期所有时间历元的状态平滑后验分布，并从后验分布中采样当前迭代周期的系统状态。
10.c2.以当前迭代周期采样出来的系统状态以及观测变量为条件，计算观测噪声方差矩阵的后验分布，并从后验分布当中采样当前迭代周期的观测噪声方差矩阵。
11.c3.以当前迭代周期采样出来的系统状态为条件，计算过程噪声方差矩阵的后验分布，并从后验分布中采样当前迭代周期的过程噪声方差矩阵。
12.d.在进行n次迭代之后，选取达到稳态之后的n-n
b
次迭代周期采样的平均值作为最终的状态估计值以及噪声方差矩阵估计值。
13.在上述方案的基础上，具体的，所述步骤a采用以下方法：
14.对于线性状态空间模型：
15.x
k
＝f
k-1
x
k-1
+w
k-1
16.z
k
＝h
k
x
k
+v
k
17.其中：为系统状态向量，为系统观测向量，为状态转移矩阵，为系统观测矩阵，为过程噪声，为观测噪声；
18.定义系统过程噪声及观测噪声满足零均值的白高斯分布，过程噪声方差矩阵及观测噪声方差矩阵恒定且未知，分别记作：
19.d(w
k
)＝q
20.d(v
k
)＝r
21.其中：d(
·
)表示随机向量的方差矩阵；
22.将过程噪声方差矩阵及观测噪声方差矩阵先验分布分别建模为其共轭先验——逆wishart分布：
23.p(q)＝iw(q；t0,t0)
24.p(r)＝iw(r；u0,u0)
25.其中：iw(x；a,a)表示随机矩阵x满足以a为自由度，以a为逆尺度矩阵的逆wishart分布；设定过程噪声方差矩阵及观测噪声方差矩阵名义值分别为q0与r0，令：
26.e(q)＝q027.e(r)＝r028.得出：
29.t0＝ρ
t
+2n+2
30.t0＝ρ
t
q031.u0＝ρ
u
+2m+2
32.u0＝ρ
u
r033.其中：ρ
u
及ρ
t
为调制参数。
34.在上述方案的基础上，具体的，所述步骤b采用以下方法：
35.根据所述步骤a得出的过程噪声方差矩阵及观测噪声方差矩阵先验分布参数t0,t0,u0,u0，直接从iw(q；t0,t0),iw(r；u0,u0)中采样得出过程噪声方差矩阵及观测噪声方差矩阵初始采样，即：
36.q
(1)
～iw(q；t0,t0)
37.r
(1)
～iw(r；u0,u0)
38.其中：a
(j)
表示随机变量a在第j次迭代当中的采样值。
39.在上述方案的基础上，具体的，所述步骤c1采用以下方法：
40.在前一迭代周期过程噪声方差矩阵采样值q
(i)
及观测噪声方差矩阵采样值r
(i)
已知的情况下，采用kalman平滑器计算状态后验分布参数：
41.在前一迭代周期过程噪声方差矩阵采样值q
(i)
及观测噪声方差矩阵采样值r
(i)
已知的情况下，采用kalman平滑器计算状态后验分布参数：
42.1)系统状态及方差初始化：
[0043][0044][0045]
其中：下标i|j代表以第j时刻之前的系统观测为条件的第i时刻的变量估计值；
[0046]
2)向前递归：
[0047]
记总的时刻数为t，对于k＝1,2,3,...t，执行如下步骤：
[0048]
a)预测
[0049]
根据k-1时刻的后验状态及后验方差计算k时刻先验状态及先验方差为：
[0050][0051]
p
k|k-1
＝f
k-1
p
k-1|k-1
f
k-1t
+q
[0052]
b)更新
[0053]
计算k时刻的后验状态及后验方差为：
[0054]
k
k
＝p
k|k-1
h
kt
(h
k
p
k|k-1
h
kt
+r)
[0055][0056]
p
k|k
＝p
k|k-1-k
k
h
k
p
k|k-1
[0057]
其中：k
k
为kalman增益；
[0058]
3)向后递归：
[0059]
对于k＝t-1,t-2,...0，执行如下步骤：
[0060][0061][0062]
p
k|t
＝p
k|k
+g
k
(p
k+1|t-p
k+1|k
)g
kt
[0063]
其中：g
k
为平滑增益；
[0064]
根据上述的kalman平滑器，得到以q
(i)
及r
(i)
为条件的状态后验参数及进而，对于k＝0,1,2,3,...t，依次按照：
[0065][0066]
进行采样，其中：n(x；a,a)表示随机向量x满足以a为均值，以a为方差的高斯分布。
[0067]
在上述方案的基础上，具体的，所述步骤c2采用以下方法：
[0068]
根据贝叶斯规则：
[0069]
p(r|z
1:t
,x
0:t
)＝cp(r)p(z
1:t
|r,x
0:t
)
[0070]
其对数形式为：
[0071]
logp(r|z
1:t
,x
0:t
)＝logp(r)+logp(z
1:t
|r,x
0:t
)+logc
[0072]
将观测噪声方差矩阵建模为逆wishart分布，其对数形式为：
[0073][0074]
根据观测模型将似然分布对数形式写作：
[0075][0076]
计算得到：
[0077][0078]
其中：
[0079][0080][0081]
也就是说，观测噪声方差的后验概率密度为以为自由度，以为逆尺度矩阵的逆wishart分布；
[0082]
进而，按照：
[0083][0084]
采样r
(i+1)
，得到当前迭代周期的观测噪声方差矩阵采样值。
[0085]
在上述方案的基础上，具体的，所述步骤c3采用以下方法：
[0086]
根据贝叶斯规则：
[0087]
p(q|x
0:t
)＝cp(q)p(x
0:t
|q)
[0088]
其对数形式为：
[0089]
logp(q|x
0:t
)＝log p(q)+logp(x
0:t
|q)+logc
[0090]
将过程噪声方差矩阵建模为逆wishart分布，其对数形式为：
[0091][0092]
根据运动学模型将似然分布对数形式写作：
[0093][0094]
计算得到：
[0095][0096]
其中：
[0097][0098][0099]
也就是说，过程噪声方差的后验概率密度为以为自由度，以为逆尺度矩阵的逆wishart分布；
[0100]
进而，按照：
[0101][0102]
采样q
(i+1)
，得到当前迭代周期的过程噪声方差矩阵采样值。
[0103]
在上述方案的基础上，具体的，所述步骤d采用以下方法：
[0104]
经历n次迭代采样后，得到状态变量采样集合为观测噪声方差矩阵采样集合为过程噪声方差矩阵采样集合为选取达到稳态之后的n-n
b
次迭代周期采样的平均值作为最终的状态估计值及噪声方差矩阵估计值，即：
[0105][0106][0107][0108]
有益效果：本发明通过gibbs采样器来对线性状态空间模型当中未知的系统状态、过程噪声方差矩阵及观测噪声方差矩阵进行随机采样，得到基于gibbs采样器的自适应平滑方法。所提出的方法可以在模型初始噪声方差矩阵误差较大时仍然取得较好的状态估计结果，同时可以较为准确的估计出未知的模型噪声方差矩阵。
附图说明
[0109]
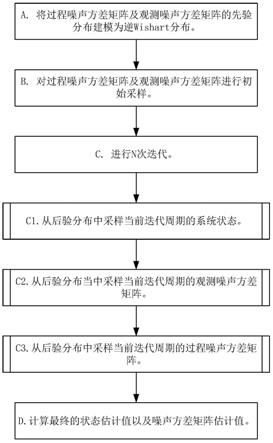
图1为本发明的流程图；
[0110]
图2为本发明即gib-ks与ks、vb-ks三种方法的位置估计均方根误差比较；
[0111]
图3为本发明即gib-ks与ks、vb-ks三种方法的速度估计均方根误差比较。
具体实施方式
[0112]
实施例1，参见附图1，一种基于gibbs采样器的自适应平滑方法，包括以下步骤：
[0113]
a.将线性状态空间模型中的过程噪声方差矩阵及观测噪声方差矩阵看作随机变量，分别将其先验分布建模为逆wishart分布。
[0114]
对于线性状态空间模型：
[0115]
x
k
＝f
k-1
x
k-1
+w
k-1
[0116]
z
k
＝h
k
x
k
+v
k
[0117]
其中：为系统状态向量，为系统观测向量，为状态转移矩阵，为系统观测矩阵，为过程噪声，为观测噪声；
[0118]
定义系统过程噪声及观测噪声满足零均值的白高斯分布，过程噪声方差矩阵及观测噪声方差矩阵恒定且未知，分别记作：
[0119]
d(w
k
)＝q
[0120]
d(v
k
)＝r
[0121]
其中：d(
·
)表示随机向量的方差矩阵；
[0122]
将过程噪声方差矩阵及观测噪声方差矩阵先验分布分别建模为其共轭先验——逆wishart分布：
[0123]
p(q)＝iw(q；t0,t0)
[0124]
p(r)＝iw(r；u0,u0)
[0125]
其中：iw(x；a,a)表示随机矩阵x满足以a为自由度，以a为逆尺度矩阵的逆wishart分布；设定过程噪声方差矩阵及观测噪声方差矩阵名义值分别为q0与r0，令：
[0126]
e(q)＝q0[0127]
e(r)＝r0[0128]
得出：
[0129]
t0＝ρ
t
+2n+2
[0130]
t0＝ρ
t
q0[0131]
u0＝ρ
u
+2m+2
[0132]
u0＝ρ
u
r0[0133]
其中：ρ
u
及ρ
t
为调制参数。
[0134]
b.在gibbs采样器框架下，对线性状态空间模型的过程噪声方差矩阵及观测噪声方差矩阵进行初始采样。
[0135]
根据所述步骤a得出的过程噪声方差矩阵及观测噪声方差矩阵先验分布参数t0,t0,u0,u0，直接从iw(q；t0,t0),iw(r；u0,u0)中采样得出过程噪声方差矩阵及观测噪声方差矩阵初始采样，即：
[0136]
q
(1)
～iw(q；t0,t0)
[0137]
r
(1)
～iw(r；u0,u0)
[0138]
其中：a
(j)
表示随机变量a在第j次迭代当中的采样值。
[0139]
c.设置总迭代周期数n以及平稳周期数n
b
，要求满足n
b
＜n；进行n次迭代，每一次迭代周期的流程为：
[0140]
c1.以上一个迭代周期采样出来的过程噪声方差矩阵及观测噪声方差矩阵为条件，基于kalman平滑器计算当前迭代周期所有时间历元的状态平滑后验分布，并从后验分布中采样当前迭代周期的系统状态。
[0141]
在前一迭代周期过程噪声方差矩阵采样值q
(i)
及观测噪声方差矩阵采样值r
(i)
已知的情况下，采用kalman平滑器计算状态后验分布参数：
[0142]
在前一迭代周期过程噪声方差矩阵采样值q
(i)
及观测噪声方差矩阵采样值r
(i)
已知的情况下，采用kalman平滑器计算状态后验分布参数：
[0143]
1)系统状态及方差初始化：
[0144][0145][0146]
其中：下标i|j代表以第j时刻之前的系统观测为条件的第i时刻的变量估计值；
[0147]
2)向前递归：
[0148]
记总的时刻数为t，对于k＝1,2,3,...t，执行如下步骤：
[0149]
a)预测
[0150]
根据k-1时刻的后验状态及后验方差计算k时刻先验状态及先验方差为：
[0151][0152]
p
k|k-1
＝f
k-1
p
k-1|k-1
f
k-1t
+q
[0153]
b)更新
[0154]
计算k时刻的后验状态及后验方差为：
[0155]
k
k
＝p
k|k-1
h
kt
(h
k
p
k|k-1
h
kt
+r)
[0156][0157]
p
k|k
＝p
k|k-1-k
k
h
k
p
k|k-1
[0158]
其中：k
k
为kalman增益；
[0159]
3)向后递归：
[0160]
对于k＝t-1,t-2,...0，执行如下步骤：
[0161][0162][0163]
p
k|t
＝p
k|k
+g
k
(p
k+1|t-p
k+1|k
)g
kt
[0164]
其中：g
k
为平滑增益；
[0165]
根据上述的kalman平滑器，得到以q
(i)
及r
(i)
为条件的状态后验参数及进而，对于k＝0,1,2,3,...t，依次按照：
[0166][0167]
进行采样，其中：n(x；a,a)表示随机向量x满足以a为均值，以a为方差的高斯分布。
[0168]
c2.以当前迭代周期采样出来的系统状态以及观测变量为条件，计算观测噪声方差矩阵的后验分布，并从后验分布当中采样当前迭代周期的观测噪声方差矩阵。
[0169]
根据贝叶斯规则：
[0170]
p(r|z
1:t
,x
0:t
)＝cp(r)p(z
1:t
|r,x
0:t
)
[0171]
其对数形式为：
[0172]
logp(r|z
1:t
,x
0:t
)＝logp(r)+logp(z
1:t
|r,x
0:t
)+logc
[0173]
将观测噪声方差矩阵建模为逆wishart分布，其对数形式为：
[0174][0175]
根据观测模型将似然分布对数形式写作：
[0176][0177]
计算得到：
[0178][0179]
其中：
[0180][0181][0182]
也就是说，观测噪声方差的后验概率密度为以为自由度，以为逆尺度矩阵的逆wishart分布；
[0183]
进而，按照：
[0184][0185]
采样r
(i+1)
，得到当前迭代周期的观测噪声方差矩阵采样值。
[0186]
c3.以当前迭代周期采样出来的系统状态为条件，计算过程噪声方差矩阵的后验分布，并从后验分布中采样当前迭代周期的过程噪声方差矩阵。
[0187]
根据贝叶斯规则：
[0188]
p(q|x
0:t
)＝cp(q)p(x
0:t
|q)
[0189]
其对数形式为：
[0190]
logp(q|x
0:t
)＝log p(q)+logp(x
0:t
|q)+logc
[0191]
将过程噪声方差矩阵建模为逆wishart分布，其对数形式为：
[0192][0193]
根据运动学模型将似然分布对数形式写作：
[0194][0195]
计算得到：
[0196][0197]
其中：
[0198][0199][0200]
也就是说，过程噪声方差的后验概率密度为以为自由度，以为逆尺度矩阵的逆wishart分布；
[0201]
进而，按照：
[0202][0203]
采样q
(i+1)
，得到当前迭代周期的过程噪声方差矩阵采样值。
[0204]
d.在进行n次迭代之后，选取达到稳态之后的n-n
b
次迭代周期采样的平均值作为最终的状态估计值以及噪声方差矩阵估计值。
[0205]
经历n次迭代采样后，得到状态变量采样集合为观测噪声方差矩阵采样集合为过程噪声方差矩阵采样集合为选取达到稳态之后的n-n
b
次迭代周期采样的平均值作为最终的状态估计值及噪声方差矩阵估计值，即：
[0206][0207][0208][0209]
实施例2，本发明实现的伪代码为：
[0210][0211]
实施例3，利用实施例1所述的自适应平滑方法通过仿真数据进行验证。
[0212]
仿真案例为二维目标跟踪，定义状态向量x
k
＝[x
k y
k v
x,k v
y,k
]
t
，其中，x
k
，y
k
，v
x,k
以及v
y,k
分别表示x与y方向的位置以及x与y方向的速度。观测变量为x与y方向的位置。系统运动学模型及观测模型分别为：
[0213][0214]
其中：δt为离散时间间隔，在本仿真中选择为1秒。总仿真时间t选择为1000秒。真实的过程噪声以及观测噪声方差矩阵设置为：
[0215][0216]
名义过程噪声方差矩阵及观测噪声方差矩阵分别设置为q
n
＝20q
t
,r
n
＝r
t
/20。仿真调制参数设置为ρ
t
＝2,ρ
u
＝2，总迭代周期n＝5000，平稳周期为n
b
＝1000。
[0217]
作为比较，本实施例同时展示了以名义噪声参数解算的kalman平滑器估计结果(ks)以及基于变分贝叶斯近似的自适应kalman平滑器估计结果(vb-ks)。本发明的方法简记作“gib-ks”。
[0218]
500独立的次monte carlo仿真的结果被用来验证本发明所提出的方法。位置和速度的均方根误差(rmse)及平均均方根误差(armse)、以及平均均方根归一化frobenius范数(asrnfn)被用来评价不同方法的性能。几种评价指标的计算方式如下：
[0219][0220][0221][0222][0223][0224][0225]
其中：及为第i次monte carlo仿真中航行器在k时刻真实的坐标；及为第i次monte carlo仿真中航行器在k时刻估计出的位置坐标；及为第i次monte carlo仿真中航行器在k时刻真实的速度；及为第i次monte carlo仿真中航行器在k时刻估计出的速度；及分别为在第i次monte carlo仿真中估计出来的过程噪声方
差矩阵及观测噪声方差矩阵。m＝500表示总的仿真次数。
[0226]
附图2为三种方法的位置估计均方误差比较，而附图3为三种方法的速度均方误差比较。三种方法的平均均方根误差以及平均均方根归一化frobenius范数如表1所示。
[0227][0228]
表1
[0229]
根据图2、图3以及表1，可以看出相比于ks与vb-ks，本发明所提出的gib-ks可以获得更好的状态估计精度，包括位置估计以及速度估计。在方差估计方面，gib-ks对过程噪声方差的估计精度差于vb-ks，而其对观测噪声方差估计的精度优于vb-ks。总体来说，所提出的gib-ks可以在噪声方差设置误差较大的情况下仍然取得较为理想的状态和方差估计结果，有较好的实际应用潜力。
[0230]
虽然，上文中已经用一般性说明及具体实施例对本发明作了详尽的描述，但在本发明基础上，可以对之作一些修改或改进，这对本领域技术人员而言是显而易见的。因此，在不偏离本发明精神的基础上所做的这些修改或改进，均属于本发明要求保护的范围。