一种具有POI结构的兰姆波谐振器的制作方法

一种具有poi结构的兰姆波谐振器
技术领域
1.本发明涉及手机射频领域，更具体地，涉及一种具有poi结构的兰姆波谐振器。


背景技术：

2.5g手机滤波器的发展要求更低损耗、更高频率和更大带宽，这对现有的声表面波(saw)和体声波(baw)技术提出了严峻的挑战，这些技术通常受到较杂散效应的限制。为了满足这一需求，最近提出的兰姆(lamb)波结构，该结构主要采用板波模式，具有较高声速，在sub
‑
6ghz及毫米波的移动通信中表现出应用优势。在兰姆波谐振器中，主模式为兰姆波，瑞利波等模式是杂散模式。杂散模式的存在会影响谐振器的性能，比如降低q值(品质因数)。如何提高机电耦合系数、抑制杂散效应是兰姆波谐振器面临的关键难题之一。


技术实现要素：

3.提供本发明内容以便以简化形式介绍将在以下具体实施方式中进一步的描述一些概念。本发明内容并非旨在标识所要求保护的主题的关键特征或必要特征，也不旨在用于帮助确定所要求保护的主题的范围。
4.为了解决上文问题，本发明旨在提供一种改进的具有poi结构的兰姆波谐振器结构，其具有高机电耦合系数和杂散小的优势。
5.根据本发明的一个方面，提供了一种具有poi结构的兰姆波谐振器，所述兰姆波谐振器包括：
6.高声速材料衬底；以及
7.位于所述高声速材料衬底上方的压电层，所述压电层的上表面和下表面上分别设置有第一和第二叉指换能器，其中所述第一和第二叉指换能器的叉指电极隔着所述压电层在层叠方向上彼此相对，且具有相同的电极宽度、电极厚度、电极间距以及激发声波波长λ，所述叉指电极均埋入所述压电层，其中
8.所述压电层的材料为切角为θ的yx
‑
linbo3，其中30
°
≤θ≤60
°
，并且所述压电层的厚度t为0.3λ－0.6λ。
9.根据本发明的进一步实施例，所述切角θ和所述压电层的厚度t的取值分别为以下组合中的一种：
10.θ＝30
°
、50
°
或60
°
，t＝0.6λ；
11.θ＝35
°
，t＝0.3λ－0.4λ或0.6λ；
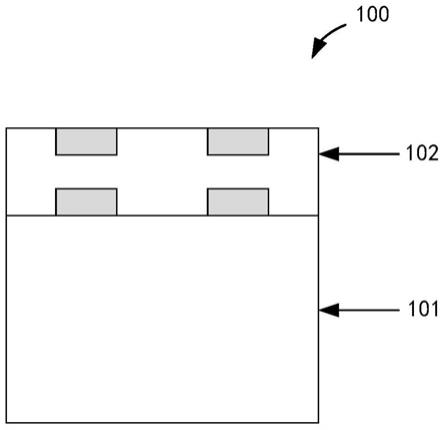
12.40
°
≤θ≤45
°
，t＝0.3λ－0.6λ；以及
13.θ＝55
°
，t＝0.5λ－0.6λ。
14.根据本发明的进一步实施例，所述切角θ和所述压电层的厚度t的取值分别为以下组合中的一种：
15.θ＝35
°
，t＝0.3λ－0.4λ；
16.θ＝50
°
，t＝0.6λ；
17.θ＝55
°
，t＝0.6λ；以及
18.θ＝60
°
，t＝0.6λ。
19.根据本发明的进一步实施例，所述高声速材料为4h
‑
sic、3c
‑
sic或6h
‑
sic。
20.根据本发明的进一步实施例，所述兰姆波谐振器进一步包括：设置在所述高声速材料衬底和所述压电层之间的低声速材料介质层。
21.根据本发明的进一步实施例，所述低声速材料为sio2，厚度为0.075λ－0.1λ。
22.根据本发明的进一步实施例，在所述压电层的与所述高声速材料衬底相对的另一侧表面上镀有一层介质层材料。
23.根据本发明的进一步实施例，所述介质层材料为sio2或sin，厚度为0.05λ－0.1λ。
24.根据本发明的进一步实施例，所述波长λ为2μm。
25.根据本发明的进一步实施例，所述高声速材料衬底的厚度为5λ，所述电极宽度为0.25λ，所述电极间距为0.25λ，并且所述电极厚度为200nm。。
26.与现有技术中的方案相比，本发明所提供的兰姆波谐振器至少具有以下优点：
27.1、通过控制压电层切角和压电层厚度，兰姆波谐振器可具有较高的机电耦合系数和高q值，且主模式无杂散或杂散很小；
28.2、通过在压电层和高声速衬底之间插入一层低声速材料介质层(例如sio2)，可以降低频率温度系数(tcf)；同时，该低声速材料介质层与高声速衬底形成反射层，防止声波从衬底方向泄露，因而使兰姆波谐振器具有高q值。
29.通过阅读下面的详细描述并参考相关联的附图，这些及其他特点和优点将变得显而易见。应该理解，前面的概括说明和下面的详细描述只是说明性的，不会对所要求保护的各方面形成限制。
附图说明
30.为了能详细地理解本发明的上述特征所用的方式，可以参照各实施例来对以上简要概述的内容进行更具体的描述，其中一些方面在附图中示出。然而应该注意，附图仅示出了本发明的某些典型方面，故不应被认为限定其范围，因为该描述可以允许有其它等同有效的方面。
31.图1是声表面波叉指换能器的结构示意图。
32.图2是示出根据本发明的一个实施例的兰姆波谐振器100的结构的横切剖面图。
33.图3是兰姆波谐振器的局部放大示意图。
34.图4(a)
‑
(d)示出了压电层切角为30
°
、压电层厚度h为0.3λ
‑
0.6λ情况下兰姆波谐振器的导纳图。
35.图5(a)
‑
(d)示出了压电层切角为35
°
、压电层厚度h为0.3λ
‑
0.6λ情况下兰姆波谐振器的导纳图。
36.图6(a)
‑
(d)示出了压电层切角为40
°
、压电层厚度h为0.3λ
‑
0.6λ情况下兰姆波谐振器的导纳图。
37.图7(a)
‑
(d)示出了压电层切角为45
°
、压电层厚度h为0.3λ
‑
0.6λ情况下兰姆波谐振器的导纳图。
38.图8(a)
‑
(d)示出了压电层切角为50
°
、压电层厚度h为0.3λ
‑
0.6λ情况下兰姆波谐
振器的导纳图。
39.图9(a)
‑
(d)示出了压电层切角为55
°
、压电层厚度h为0.3λ
‑
0.6λ情况下兰姆波谐振器的导纳图。
40.图10(a)
‑
(d)示出了压电层切角为60
°
、压电层厚度h为0.3λ
‑
0.6λ情况下兰姆波谐振器的导纳图。
41.图11是示出根据本发明的另一实施例的兰姆波谐振器200的结构的横切剖面图。
具体实施方式
42.下面结合附图详细描述本发明，本发明的特点将在以下的具体描述中得到进一步的显现。
43.图1是声表面波叉指换能器(idt)的结构示意图。如图1中所示，在压电基片的表面上，沉积一层金属薄膜，再利用半导体平面工艺中的光刻方法得到一组梳形的交叉的金属电极。这些形如人指的金属电极相互交叉配置，两端有汇流条连接在一起分别形成器件的两级，从而得到叉指换能器。在图1的示例中，共示出标号1－6的6个金属电极，表明这个叉指换能器的叉指电极数是6，其中奇数标号(1、3、5)的电极(又称指条)相连在一起，构成叉指换能器的正输入(或输出)端点(图中+v)，偶数标号(2、4、6)的电极的指条连在一起，构成叉指换能器的正输入(或输出)端点(图中－v)。
44.声表面波叉指换能器的几个主要参数是：指对数n(例如，图1中的指对数n＝3)，金属指条的宽度d，半周期长度l，相邻指条的间隙宽度b(b＝l－d)。
45.图2是示出根据本发明的一个实施例的兰姆波谐振器100的结构的将兰姆波谐振器沿例如图1中所示的中线a
‑
a横切后的剖面示意图。如图2中所示，兰姆波谐振器100可包括衬底101，该衬底101可使用高声速材料，例如4h
‑
sic或6h
‑
sic，并构成poi结构。
46.在衬底101的上方是压电层102，在压电层102的上表面和下表面上分别设置有第一和第二叉指换能器(idt)，其中第一和第二叉指换能器的叉指电极(也可简称为上电极和下电极)分别隔着压电层102在层叠方向上彼此相对，并且具有相同的电极宽度、电极厚度、电极间距以及激发声波波长λ。在本示例中，各叉指电极完全埋入压电层中。作为一个示例，压电层102的材料可以是切角为θ的yx
‑
linbo3，切角θ可以在例如30
°‑
60
°
。第一和第二叉指换能器的叉指电极可由ti、al、cu、au、pt、ag、pd、ni等金属或合金、或者这些金属或合金的层叠体构成。本领域技术人员可以理解，虽然在图2中上电极和下电极都只示出了两个电极指，但这仅仅是方便解说，实际上一个兰姆波谐振器的叉指电极通常具有两个以上的电极指(如图1所示)，这些电极指均具有相同的电极宽度、电极厚度、电极间距以及激发声波波长λ。
47.图3是兰姆波谐振器的局部放大示意图。如图3中所示，上下电极均被完全埋入压电层102中，电极的厚度均为200nm。电极宽度与电极间距的和可以为0.5λ，其中λ为电极的激发声波波长。电极宽度可以为0.25λ。此外，作为参考，在本示例中，λ可以为2μm，衬底101的厚度为5λ。压电层102的厚度可以为0.3λ
‑
0.6λ。
48.在过往的针对机电耦合系数和杂散效应的改善方面的尝试中，从未考虑和探索过电极埋入压电层的比例对机电耦合系数和杂散效应的影响，更未考虑和探索过在电极完全埋入压电层的情况下，压电层厚度和压电层切角的组合对机电耦合系数和杂散效应的影
响。图4－10分别示出了不同压电层切角和不同压电层厚度情况下兰姆波谐振器的导纳图，在这些图中，占空比为η，f
s
为谐振频率，fp为反谐振频率，中心频率f0可按以下公式(1)计算：
49.f0＝(f
s
+fp)/2
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(1)
50.机电耦合系数k2，可按以下公式(2)计算：
51.k2＝(π2/8)(fp2‑
f
s2
)/f
s2
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(2)
52.图4(a)示出了压电层切角为30
°
、压电层厚度h为0.3λ情况下的导纳图。如图4(a)中所示，在压电层切角为30
°
、压电层厚度h为0.3λ的情况下，谐振频率f
s
为约2350mhz，反谐振频率f
p
为约2716mhz，此时根据公式(2)，可计算出机电耦合系数k2为约41.38％。
53.图4(b)示出了压电层切角为30
°
、压电层厚度h为0.4λ情况下的导纳图。如图4(b)中所示，在压电层切角为30
°
、压电层厚度h为0.4λ的情况下，谐振频率f
s
为约2188mhz，反谐振频率f
p
为约2587mhz，此时根据公式(2)，可计算出机电耦合系数k2为约49.05％。
54.图4(c)示出了压电层切角为30
°
、压电层厚度h为0.5λ情况下的导纳图。如图4(c)中所示，在压电层切角为30
°
、压电层厚度h为0.5λ的情况下，谐振频率f
s
为约2120mhz，反谐振频率f
p
为约2509mhz，此时根据公式(2)，可计算出机电耦合系数k2为约49.38％。
55.图4(d)示出了压电层切角为30
°
、压电层厚度h为0.6λ情况下的导纳图。如图4(d)中所示，在压电层切角为30
°
、压电层厚度h为0.6λ的情况下，谐振频率f
s
为约2153mhz，反谐振频率f
p
为约2514mhz，此时根据公式(2)，可计算出机电耦合系数k2为约44.79％。
56.图5(a)示出了压电层切角为35
°
、压电层厚度h为0.3λ情况下的导纳图。如图5(a)中所示，在压电层切角为35
°
、压电层厚度h为0.3λ的情况下，谐振频率f
s
为约2354mhz，反谐振频率f
p
为约2723mhz，此时根据公式(2)，可计算出机电耦合系数k2为约41.67％。
57.图5(b)示出了压电层切角为35
°
、压电层厚度h为0.4λ情况下的导纳图。如图5(b)中所示，在压电层切角为35
°
、压电层厚度h为0.4λ的情况下，谐振频率f
s
为约2193mhz，反谐振频率f
p
为约2595mhz，此时根据公式(2)，可计算出机电耦合系数k2为约49.33％。
58.图5(c)示出了压电层切角为35
°
、压电层厚度h为0.5λ情况下的导纳图。如图5(c)中所示，在压电层切角为35
°
、压电层厚度h为0.5λ的情况下，谐振频率f
s
为约2123mhz，反谐振频率f
p
为约2516mhz，此时根据公式(2)，可计算出机电耦合系数k2为约49.85％。
59.图5(d)示出了压电层切角为35
°
、压电层厚度h为0.6λ情况下的导纳图。如图5(d)中所示，在压电层切角为35
°
、压电层厚度h为0.6λ的情况下，谐振频率f
s
为约2160mhz，反谐振频率f
p
为约2521mhz，此时根据公式(2)，可计算出机电耦合系数k2为约44.64％。
60.图6(a)示出了压电层切角为40
°
、压电层厚度h为0.3λ情况下的导纳图。如图6(a)中所示，在压电层切角为40
°
、压电层厚度h为0.3λ的情况下，谐振频率f
s
为约2360mhz，反谐振频率f
p
为约2726mhz，此时根据公式(2)，可计算出机电耦合系数k2为约41.19％。
61.图6(b)示出了压电层切角为40
°
、压电层厚度h为0.4λ情况下的导纳图。如图6(b)中所示，在压电层切角为40
°
、压电层厚度h为0.4λ的情况下，谐振频率f
s
为约2200mhz，反谐振频率f
p
为约2599mhz，此时根据公式(2)，可计算出机电耦合系数k2为约48.76％。
62.图6(c)示出了压电层切角为40
°
、压电层厚度h为0.5λ情况下的导纳图。如图6(c)中所示，在压电层切角为40
°
、压电层厚度h为0.5λ的情况下，谐振频率f
s
为约2130mhz，反谐振频率f
p
为约2520mhz，此时根据公式(2)，可计算出机电耦合系数k2为约49.26％。
63.图6(d)示出了压电层切角为40
°
、压电层厚度h为0.6λ情况下的导纳图。如图6(d)中所示，在压电层切角为40
°
、压电层厚度h为0.6λ的情况下，谐振频率f
s
为约2170mhz，反谐振频率f
p
为约2525mhz，此时根据公式(2)，可计算出机电耦合系数k2为约43.62％。
64.图7(a)示出了压电层切角为45
°
、压电层厚度h为0.3λ情况下的导纳图。如图7(a)中所示，在压电层切角为45
°
、压电层厚度h为0.3λ的情况下，谐振频率f
s
为约2368mhz，反谐振频率f
p
为约2725mhz，此时根据公式(2)，可计算出机电耦合系数k2为约39.96％。
65.图7(b)示出了压电层切角为45
°
、压电层厚度h为0.4λ情况下的导纳图。如图7(b)中所示，在压电层切角为45
°
、压电层厚度h为0.4λ的情况下，谐振频率f
s
为约2207mhz，反谐振频率f
p
为约2599mhz，此时根据公式(2)，可计算出机电耦合系数k2为约47.67％。
66.图7(c)示出了压电层切角为45
°
、压电层厚度h为0.5λ情况下的导纳图。如图7(c)中所示，在压电层切角为45
°
、压电层厚度h为0.5λ的情况下，谐振频率f
s
为约2139mhz，反谐振频率f
p
为约2519mhz，此时根据公式(2)，可计算出机电耦合系数k2为约47.68％。
67.图7(d)示出了压电层切角为45
°
、压电层厚度h为0.6λ情况下的导纳图。如图7(d)中所示，在压电层切角为45
°
、压电层厚度h为0.6λ的情况下，谐振频率f
s
为约2180mhz，反谐振频率f
p
为约2526mhz，此时根据公式(2)，可计算出机电耦合系数k2为约42.23％。
68.图8(a)示出了压电层切角为50
°
、压电层厚度h为0.3λ情况下的导纳图。如图8(a)中所示，在压电层切角为50
°
、压电层厚度h为0.3λ的情况下，谐振频率f
s
为约2377mhz，反谐振频率f
p
为约2720mhz，此时根据公式(2)，可计算出机电耦合系数k2为约38.13％。
69.图8(b)示出了压电层切角为50
°
、压电层厚度h为0.4λ情况下的导纳图。如图8(b)中所示，在压电层切角为50
°
、压电层厚度h为0.4λ的情况下，谐振频率f
s
为约2216mhz，反谐振频率f
p
为约2595mhz，此时根据公式(2)，可计算出机电耦合系数k2为约45.76％。
70.图8(c)示出了压电层切角为50
°
、压电层厚度h为0.5λ情况下的导纳图。如图8(c)中所示，在压电层切角为50
°
、压电层厚度h为0.5λ的情况下，谐振频率f
s
为约2149mhz，反谐振频率f
p
为约2515mhz，此时根据公式(2)，可计算出机电耦合系数k2为约45.56％。
71.图8(d)示出了压电层切角为50
°
、压电层厚度h为0.6λ情况下的导纳图。如图8(d)中所示，在压电层切角为50
°
、压电层厚度h为0.6λ的情况下，谐振频率f
s
为约2192mhz，反谐振频率f
p
为约2522mhz，此时根据公式(2)，可计算出机电耦合系数k2为约39.90％。
72.图9(a)示出了压电层切角为55
°
、压电层厚度h为0.3λ情况下的导纳图。如图9(a)中所示，在压电层切角为55
°
、压电层厚度h为0.3λ的情况下，谐振频率f
s
为约2387mhz，反谐振频率f
p
为约2711mhz，此时根据公式(2)，可计算出机电耦合系数k2为约35.73％。
73.图9(b)示出了压电层切角为55
°
、压电层厚度h为0.4λ情况下的导纳图。如图9(b)中所示，在压电层切角为55
°
、压电层厚度h为0.4λ的情况下，谐振频率f
s
为约2225mhz，反谐振频率f
p
为约2587mhz，此时根据公式(2)，可计算出机电耦合系数k2为约43.37％。
74.图9(c)示出了压电层切角为55
°
、压电层厚度h为0.5λ情况下的导纳图。如图9(c)中所示，在压电层切角为55
°
、压电层厚度h为0.5λ的情况下，谐振频率f
s
为约2162mhz，反谐振频率f
p
为约2508mhz，此时根据公式(2)，可计算出机电耦合系数k2为约42.60％。
75.图9(d)示出了压电层切角为55
°
、压电层厚度h为0.6λ情况下的导纳图。如图9(d)中所示，在压电层切角为55
°
、压电层厚度h为0.6λ的情况下，谐振频率f
s
为约2204mhz，反谐振频率f
p
为约2515mhz，此时根据公式(2)，可计算出机电耦合系数k2为约37.24％。
76.图10(a)示出了压电层切角为60
°
、压电层厚度h为0.3λ情况下的导纳图。如图10(a)中所示，在压电层切角为60
°
、压电层厚度h为0.3λ的情况下，谐振频率f
s
为约2399mhz，反谐振频率f
p
为约2700mhz，此时根据公式(2)，可计算出机电耦合系数k2为约32.87％。
77.图10(b)示出了压电层切角为60
°
、压电层厚度h为0.4λ情况下的导纳图。如图10(b)中所示，在压电层切角为60
°
、压电层厚度h为0.4λ的情况下，谐振频率f
s
为约2233mhz，反谐振频率f
p
为约2576mhz，此时根据公式(2)，可计算出机电耦合系数k2为约40.77％。
78.图10(c)示出了压电层切角为60
°
、压电层厚度h为0.5λ情况下的导纳图。如图10(c)中所示，在压电层切角为60
°
、压电层厚度h为0.5λ的情况下，谐振频率f
s
为约2177mhz，反谐振频率f
p
为约2497mhz，此时根据公式(2)，可计算出机电耦合系数k2为约38.89％。
79.图10(d)示出了压电层切角为60
°
、压电层厚度h为0.6λ情况下的导纳图。如图10(d)中所示，在压电层切角为60
°
、压电层厚度h为0.6λ的情况下，谐振频率f
s
为约2216mhz，反谐振频率f
p
为约2503mhz，此时根据公式(2)，可计算出机电耦合系数k2为约33.99％。
80.以下的表1中，统计了上述各图中所示的不同压电层切角以及不同压电层厚度下兰姆波谐振器的谐振频率f
s
、反谐振频率fp、声波速度以及机电耦合系数k2的表现，同时还给出了每一种情况下的q值。
81.[0082][0083]
表1
[0084]
可以发现，在不同的压电层切角θ和压电层厚度h的不同组合下，以下几组取值具有明显的改善机电耦合系数和品质因素q值得效果。
[0085]
1、当压电层切角θ和电极压电层厚度h为表2中的数值时，兰姆波谐振器的机电耦合系数较大，至少在34％以上，且主模式无杂散或杂散很小。
[0086]
压电层切角θ(yx
‑
linbo3)压电层厚度(λ)机电耦合系数k2(％)30
°
,50,60
°
0.6k2≥34％35
°
[0.3,0.4],0.6k2≥41.6％[40
°
,45
°
][0.3,0.6]k2≥40％
55
°
[0.5,0.6]k2≥37.2％
[0087]
表2
[0088]
2、当压电层切角θ和电极压电层厚度h为表3中的数值时，兰姆波谐振器的机电耦合系数较大，至少在37.2％以上，且主模式无杂散或杂散很小，这意味着杂散效应被抑制，从数据中可见，此时的品质因数q的值很高，至少在535以上。
[0089][0090]
表3
[0091]
图11是示出根据本发明的另一实施例的兰姆波谐振器200的结构的横切剖面图。如图11中所示，兰姆波谐振器200具有与兰姆波谐振器100类似地结构，不同之处在于，在高声速衬底101和压电层102之间插入了一层介质层103。介质层103可由具有低声速的低声阻抗材料构成，例如sio2。这一介质层103的频率温度系数为正，而压电层102的频率温度系数为负，因此这一介质层103可以降低兰姆波谐振器的频率温度系数(tcf)。此外，介质层103具有低声速，与高声速衬底101形成反射层，从而可以防止声波从衬底101的方向泄露，这一步有助于获得高q值。作为一个示例，介质层103的厚度可以为0.075
‑
0.1λ。
[0092]
可选地，兰姆波谐振器可进一步在压电层102的上方采用pecvd、cvd等方式再覆盖一层介质层，该介质层的材料可以是sio2、sin等。这一介质层可进一步降低兰姆波谐振器的频率温度系数(tcf)，并且还可以同时作为谐振器的保护层。
[0093]
以上所已经描述的内容包括所要求保护主题的各方面的示例。当然，出于描绘所要求保护主题的目的而描述每一个可以想到的组件或方法的组合是不可能的，但本领域内的普通技术人员应该认识到，所要求保护主题的许多进一步的组合和排列都是可能的。从而，所公开的主题旨在涵盖落入所附权利要求书的精神和范围内的所有这样的变更、修改和变化。