一种基于加权概率模型的无损压缩方法和无损解压方法与流程

1.本发明涉及通信编码技术领域，特别涉及一种基于加权概率模型的无损压缩方法和无损解压方法。


背景技术：

2.大数据时代，数据量快速增长给网络传输和存储带来巨大压力。为了解决这一问题，一方面需提升硬件设施，另一方面是挖掘具有更高压缩率的无损编码算法。常见的无损压缩方法有字典编码、行程编码、算术编码等，统称为熵编码，但目前的熵编码还存在有以下缺陷：
3.1)根据最大熵定理，均匀分布的二进制序列将无法进行无损压缩，现有的熵编码均遵从该定理；2)压缩率较低而且对硬件资源的需求高。


技术实现要素：

4.本发明旨在至少解决现有技术中存在的技术问题之一。为此，本发明提出一种基于加权概率模型的无损压缩方法和无损解压方法。对均匀分布的二进制序列进行等长无损降熵处理，使得均匀分布的二进制序列可以进行无损压缩；提升了压缩率，硬件资源需求少，压缩率由等长无损降熵所使用的权系数决定。
5.本发明的第一方面，提供了一种基于加权概率模型的无损压缩方法，包括以下步骤：
6.将序列长度为n且符号均匀分布的二进制序列x等长无损降熵为序列长度为所述n的二进制序列y，其中所述等长无损降熵过程所使用的第一权系数r1的取值范围为：r1∈[0.5，1.0)；
[0007]
通过加权概率模型将所述二进制序列y无损压缩为二进制序列z，其中所述加权概率模型所使用的第二权系数r2的取值为：r2＝1。
[0008]
本发明的第二方面，提供了一种基于加权概率模型的无损解压方法，应用于本发明第一方面所述的基于加权概率模型的无损压缩方法，包括以下步骤：
[0009]
通过加权概率模型将所述二进制序列z无损解压为所述二进制序列y；
[0010]
将所述二进制序列y等长无损增熵变换成所述二进制序列x。
[0011]
本发明的第三方面，提供了一种编码设备，包括：至少一个控制处理器和用于与所述至少一个控制处理器通信连接的存储器；所述存储器存储有可被所述至少一个控制处理器执行的指令，所述指令被所述至少一个控制处理器执行，以使所述至少一个控制处理器能够执行如本发明第一方面所述的基于加权概率模型的无损压缩方法和/或本发明第二方面所述的基于加权概率模型的无损解压方法。
[0012]
本发明的第四方面，提供了一种计算机可读存储介质，其特征在于，所述计算机可读存储介质存储有计算机可执行指令，所述计算机可执行指令用于使计算机执行如本发明第一方面所述的基于加权概率模型的无损压缩方法和/或本发明第二方面所述的基于加权
概率模型的无损解压方法。
[0013]
根据本发明的实施例，至少具有以下有益效果：
[0014]
本发明提供了一种基于加权概率模型的无损压缩方法，根据最大熵定理，均匀分布的二进制序列将无法再进行无损压缩，现有的熵编码均遵从该定理。本方法的核心是提供了一种等长无损降熵变换的过程，因为对均匀分布的二进制序列进行了等长无损降熵处理，所以使得均匀分布的二进制序列可以进行无损压缩。压缩率与自定义的权系数有关。显然本方法的压缩率优于现有的熵编码算法。而且由于本方法是以比特为单位的编译码过程，无需大量的硬件缓存和编码，且可以分段并行处理，所以运算的硬件资源少。本发明还基于本无损压缩方法提供了一种基于加权概率模型的无损压缩方法，实现了本无损压缩方法的逆过程。
[0015]
本发明的附加方面和优点将在下面的描述中部分给出，部分将从下面的描述中变得明显，或通过本发明的实践了解到。
附图说明
[0016]
本发明的上述和/或附加的方面和优点从结合下面附图对实施例的描述中将变得明显和容易理解，其中：
[0017]
图1为本发明实施例提供的当n＝1时x1＝0，1，...，k的f(x，r)的示意图；
[0018]
图2为本发明实施例提供的当n＝2且已知x1时，x2＝0，1，...，k的f(x，r)的示意图；
[0019]
图3为本发明实施例提供的一种基于加权概率模型的无损压缩方法的流程示意图；
[0020]
图4为本发明实施例提供的一种基于加权概率模型的无损解压方法的流程示意图；
[0021]
图5为本发明实施例提供的一种编码设备的结构示意图。
具体实施方式
[0022]
下面详细描述本发明的实施例，所述实施例的示例在附图中示出，其中自始至终相同或类似的标号表示相同或类似的元件或具有相同或类似功能的元件。下面通过参考附图描述的实施例是示例性的，仅用于解释本发明，而不能理解为对本发明的限制。
[0023]
为了便于本领域技术人员理解本发明的技术方案，在介绍本申请实施例之前，首先对本申请中涉及的相关概念进行解释说明：
[0024]
一、加权概率以及加权概率模型；
[0025]
令x＝{x1，x2，...，x
n
}是有限个值或可数个可能值的随机过程。除非特别声明，这个随机过程的可能值的集合都将记为非负整数的集合a＝{0，1，2，...，s}，即x
i
∈a(i＝1，2，...，n)。于是对于a中一切数值有概率空间：
[0026][0027]
其中x∈a。由于随机过程必须转移到集合a中的某个数值，所以在任意时刻i有：
[0028][0029]
其中0≤p(x)≤1。于是，任意时刻i累积分布函数f(a)可以用p(x)表示为：
[0030]
f(a)＝∑
x≤a p(x)
ꢀꢀꢀ
(3)
[0031]
其中0≤f(a)≤1，a∈a。这里提供一组示例：若离散随机变量x具有概率质量函数p(0)＝0.5，p(1)＝0.3，p(2)＝0.2，则f(0)＝p(0)＝0.5，f(1)＝p(0)+p(1)＝0.8，f(2)＝p(0)+p(1)+p(2)＝1.0。
[0032]
设x
i
为伯努利随机变量，则x
i
∈{0，1}，x
i
的概率质量函数p(0)＝p(x
i
＝0)＝1
‑
p，p(1)＝p(x
i
＝1)＝p，其中0≤p≤1，i＝1，2，...，n。随机过程x存在2
n
种可能性，且每个x都是长度为n的二进制序列。显然，2
n
种可能性中，部分二进制序列存在很明显的形态特征(规律)。例如：一些二进制序列满足“序列中连续符号1的个数最多为t个”。又比如一些二进制序列满足“序列中连续符号1的个数最多为t个，且序列中连续符号0的个数最多为s个”。由于形态特征已知，所以t和s为已知可数的正整数。其中，伯努利随机变量为：假定一个试验，分别用x＝1和x＝0代表试验结果的成功与失败；x的概率质量函数为p(0)＝p(x＝0)＝1
‑
p，p(1)＝p(x＝1)＝p，其中p(0≤p≤1)为试验结果成功的概率；随机变量x称为伯努利随机变量。
[0033]
因此，当随机过程x呈现某种已知的形态特征时，其在信息编码技术领域有如下应用：
[0034]
(1)数据压缩；因为二进制序列中t个连续的符号1后必然出现一个符号0，则二进制序列的形态特征为已知的信息，去除该符号0后进行无损编码可提升压缩效果。即不同形态特征的二进制序列采用不同的方法去除冗余信息。
[0035]
(2)数据校验；若译码出的二进制序列不满足“序列中连续符号1的个数最多为t个”，则译码出错，于是可用于数据校验。不同的形态特征，可构造不同码率的信道编码方法。
[0036]
(3)数字水印；通过改造任意二进制序列，使其满足某一形态特征。然后进行无损编码，从而构造数字水印编码方法。
[0037]
显然，此类二进制序列(即随机过程)中，当前符号状态与之前相邻有限个符号状态有关。
[0038]
以二进制序列满足形态特征“序列中连续符号1的个数最多为2个”为例，该序列是由“0”，“10”和“110”组成。基于马尔可夫链或条件概率分析，符号0存在三种概率质量函数，分别为p(0|0)，p(0|1)，p(0|1，1)。符号1存在两种概率质量函数，分别为p(1|0)和p(1|1)。编码时，因为二进制序列作为信源是已知的，所以每个符号使用的概率质量函数均能准确选择。但是译码时无法准确选择概率质量函数，比如已经译码出“0”(首个符号译码时可约定概率质量函数)，因符号0存在三种概率质量函数，无法正确选择。同理符号1也无法正确选择概率质量函数。若已经译码出“01”，因存在两种概率质量函数p(1|1)或p(0|1)，所以通过已经译码的结果来推测下一个符号也不可行。当已经译码出“011”，因“011”后必然是符号0，所以存在唯一的选择p(0|1，1)。
[0039]
当编码后的数据被篡改或传输出错时，每个符号均可能译码错误，采用马尔可夫链或条件概率构造编译码方法不可行。总结上述原因，基于概率定理，为该类二进制序列构造编译码方法需满足三个条件：
[0040]
(1)每译码一个符号x存在唯一已知的概率质量函数p(x)，p(x)可以是由译码(编码的逆过程)结果推测出唯一已知的概率质量函数，例如已经译码出“011”，因“011”后必然
是符号0，所以存在唯一的概率质量函数p(x)＝p(0|1，1)。
[0041]
(2)存在一个表征着序列形态特征的已知变量r，也可以是已知函数f(i)(i＝1，2，...，n)的值，即r＝f(i)。序列的形态特征不同，r的值也应当不同。
[0042]
(3)编译码时r应当作用于序列每个位置对应符号的概率质量函数。
[0043]
可定义函数来构造编译码方法，如(或)，(或)等，则整个编译码过程均可准确选择概率质量函数和r。本发明称r为概率质量函数的形态特征系数，简称权系数。由于(或)，使得产生多项式不方便推理和分析，所以下面基于定义加权概率质量函数和加权累积分布函数，并通过分析这两个函数得出r的数理性质。因p(x)和r已知，并且因x不同而不同，所以可简单标记为
[0044]
定义1、加权概率质量函数为：
[0045][0046]
p(a)为a的概率质量函数，0≤p(a)≤1，r为权系数，r是已知的正实数。显然，所有符号的加权概率之和为：
[0047][0048]
定义2、加权累积分布函数(简称加权分布函数)为：
[0049]
f(a，r)＝rf(a)＝r∑
x≤a p(x)
ꢀꢀꢀ
(6)
[0050]
根据定义2，将序列x的加权分布函数记为f(x，r)。令n＝1时f(x，r)为：
[0051]
f(x，r)＝rf(x1)＝rf(x1‑
1)+rp(x1)
[0052]
如图1所示，n＝2时，选择x1对应的区间[f(x1‑
1，r)，f(x1，r))，由于f(x1，r)＝f(x1‑
1，r)+rp(x1)，所以区间长度为)，所以区间长度为然后，将区间[f(x1‑
1，r)，f(x1‑
1，r)+rp(x1))的长度乘以权系数r，若r＜1时，区间缩小；若r＞1时区间扩大；若r＝1时区间不变。于是区间变成了[f(x1‑
1，r)，f(x1‑
1，r)+r2p(x1))，接着将r2p(x1)按照式(1)中各符号的概率质量分割成k+1份，分割后符号0对应区间为[f(x1‑
1，r)，f(x1‑
1，r)+r2p(x1)p(0))；符号1对应的区间为[f(x1‑
1，r)+r2p(x1)p(0)，f(x1‑
1，r)+r2p(x1)(p(0)+p(1)))；符号2对应的区间为[f(x1‑
1，r)+r2p(x1)(p(0)+p(1))，f(x1‑
1，r)+r2p(x1)(p(0)+p(1)+p(2)))，类推且f(x1‑
1，r)＝rf(x1‑
1)，得：
[0053]
f(x，r)＝rf(x1‑
1)+r2f(x2)p(x1)＝rf(x1‑
1)+r2f(x2‑
1)p(x1)+r2p(x1)p(x2)
[0054]
此时，区间长度为r2p(x1)p(x2)。如图2所示：
[0055]
类推，n＝3时：
[0056]
f(x，r)＝rf(x1‑
1)+r2f(x2‑
1)p(x1)+r3f(x3)p(x1)p(x2)＝rf(x1‑
1)+r2f(x2‑
1)p(x1)+r3f(x3‑
1)p(x1)p(x2)+r3p(x1)p(x2)p(x3)
[0057]
于是，令类推可得：
[0058][0059]
将满足式(7)的加权分布函数的集合定义为加权概率模型，简称加权模型，记为{f(x，r)}。若x
i
∈a＝{0，1}，则称{f(x，r)}为二元加权模型。令：
[0060]
h
n
＝f(x，r)
ꢀꢀꢀ
(8)
[0061][0062][0063]
因x
i
必须取a中的值，所以p(x
i
)≥0。显然式(8)至(10)为区间列，l
i
，h
i
是序列x在时刻i(i＝1，2，...，n)变量x
i
对应的区间上下标，r
i
＝h
i
‑
l
i
是区间的长度。{[l
n
，h
n
)}为定义在加权概率模型上的区间列。将式(8)至(10)用迭代式表达为：
[0064][0065]
l
i
＝l
i
‑1+r
i
‑1f(x
i
‑
1，r)
ꢀꢀꢀ
(12)
[0066]
h
i
＝l
i
+r
i
ꢀꢀꢀ
(13)
[0067]
显然，式(7)中r为已知实数，将(7)称为静态加权模型。若r在时刻i等于已知函数值ω
i
，即ω
i
＝f(i)，f(i)为已知函数，于是系数序列为w＝{ω1，ω2，...，ω
n
}，则(7)可表达为：
[0068][0069]
满足式(14)的加权分布函数的集合称为动态加权模型。当ω1＝ω2＝
…
＝ω
n
＝r时，f(x，w)＝f(x，r)。若ω1＝ω2＝
…
＝ω
n
＝r＝1，则f(x，w)＝f(x，1)＝f(x)。
[0070][0071]
基于式(15)的迭代式为：
[0072]
r
i
＝r
i
‑1p(x
i
)
ꢀꢀꢀ
(16)
[0073]
l
i
＝l
i
‑1+r
i
‑1f(x
i
‑
1)
ꢀꢀꢀ
(17)
[0074]
h
i
＝l
i
+r
i
ꢀꢀꢀ
(18)
[0075]
于是有定理1、若权系数ω
i
(i＝1，2，...，n)满足0＜ω
i
≤1时，≤1时，成立。
[0076]
定理1的证明过程如下：
[0077]
∵0＜ω
i+1
≤1，由式(11)至(13)得r
i+1
＝r
i
ω
i+1
p(x
i+1
)；
[0078]
∴0＜r
i+1
≤r
i
p(x
i+1
)；
[0079]
∵l
i+1
＝l
i
+r
i
ω
i+1
f(x
i+1
‑
1)，其中r
i
ω
i+1
f(x
i+1
‑
1)≥0；
[0080]
∴l
i+1
≥l
i
；
[0081]
∵h
i+1
＝l
i+1
+r
i+1
，且r
i+1
＞0；
[0082]
∴l
i+1
＜h
i+1
；
[0083]
∵h
i+1
＝l
i
+r
i
ω
i+1
f(x
i+1
‑
1)+r
i
p(x
i+1
)＜l
i
+r
i
(f(x
i+1
‑
1)+p(x
i+1
))；
[0084]
∵f(x
i+1
)＝f(x
i+1
‑
1)+p(x
i+1
)，由于f(x
i+1
)≤ω
i+1
，且ω
i+1
≤1；
[0085]
∴h
i+1
≤l
i
+r
i
＝h
i
；
[0086]
根据定理1，通过归纳法可得定理2：
[0087]
定理2、任意i＝1，2，...，n，若权系数ω
i
满足0＜ω
i
≤1，有≤1，有
[0088]
任意i有ω
i
＝1，则称{f(x，w)}为标准模型；任意i有0＜ω
i
≤1且存在ω
i
＜1，则称{f(x，w)}为收缩模型；任意i有ω
i
≥1且存在ω
i
＞1，则称{f(x，w)}为扩张模型。
[0089]
二、加权概率模型的信息熵；
[0090]
设离散无记忆信源序列x＝(x1，x2，...，x
n
)(x
i
∈a，a＝{0，1，2，...，s})，当权系数r＝1时，由所以由香农信息熵定义，x的熵为(对数以s+1为底)：
[0091][0092]
当r≠1时，定义具有概率的随机变量x
i
的自信息量为：
[0093][0094]
设集合{x
i
＝a}(i＝1，2，...，n；a∈a)中有c
a
个a。当r已知，信源序列x的总信息量为：
[0095][0096]
于是平均每个符号的信息量为：
[0097][0098]
定义3、令h(x，r)为加权模型信息熵(单位为：比特/符号)：
[0099][0100]
于是有定理3、离散无记忆信源序列x＝(x1，x2，...，x
n
)(x
i
∈a，a＝{0，1，2，...，s}，i＝1，2，...，n)通过加权概率模型无失真编码，最小极限为h(x，r
max
)(r
max
为最大权系数)。
[0101][0102]
定理3的证明过程如下：
[0103]
任意r＞r
max
时，l
n
∈[l
n
，h
n
)∧l
n
∈[l
n
‑1，h
n
‑1)∧
…
∧l
n
∈[l
i
，h
i
)不成立，即无法还原序列x。当0＜r≤1时，
‑
log r≥0，有h(x，r)≥h(x)；当1＜r≤r
max
时，
‑
log r＜0，有h(x，r)＜h(x)，显然最小极限值为h(x，r)＝
‑
log r
max
+h(x)。
[0104]
定理3给出的是静态加权模型的信息熵。而在动态加权模型中，当系数序列w＝{ω1，ω2，...，ω
n
}已知时，根据独立离散随机序列x，其加权概率为：
[0105]
[0106]
根据对数运算法则可得：
[0107][0108]
由于集合{x
i
＝a}(i＝1，2，...，n；a∈a)中有c
a
个a，所以：
[0109][0110]
显然，式(26)可变换为：
[0111][0112]
然后将式(28)平均到每个符号，则有：
[0113][0114]
因所以于是：
[0115][0116]
令
[0117][0118]
可得h(x，w)＝
‑
logr
‑
h(x)。当r≤r
max
时，l
n
∈[l
n
，h
n
)∧l
n
∈[l
n
‑1，h
n
‑1)∧
…
∧l
n
∈[l
i
，h
i
)成立。
[0119]
本发明的实施例；
[0120]
根据上述现有理论：设长度为n的任意二进制序列x，其中符号0和符号1的概率为p(0)和p(1)。根据信息论，序列x的信息熵h(x)＝
‑
p(0)log
2 p(0)
‑
p(1)log
2 p(1)。设加权概率模型编码后的结果为n，根据上式(23)有：
[0121]
‑
n log
2 r+nh(x)＝n
ꢀꢀꢀ
(32)
[0122]
化简可得：
[0123]
r＝2
h(x)
‑1ꢀꢀꢀ
(33)
[0124]
因0≤h(x)≤1，所以0.5≤r≤1.0。根据上述定理2，因为因0≤h(x)≤1，所以0.5≤r≤1.0。根据上述定理2，因为且[l
i
，h
i
)唯一的与符号x
i
对应，所以可无损译码。以图1和图2为例，因为所以解码出x1。同理解码出x2。显然，加权概率模型编码算法是无损的。于是通过式(32)，加权概率模型可以将二进制序列x无损的转换为等长度的二进制序列y。
[0125]
于是得出结论一：二进制序列y中符号均匀分布，即p(0)＝p(1)＝0.5。
[0126]
结论一的证明过程如下：根据信息论，序列y的信息熵为h(y)＝
‑
p(0)log
2 p(0)
‑
p(1)log
2 p(1)。因序列y为加权概率模型无损编码后的结果，所以h(y)＝h(x，r)。由于序列x和y等长，所以有nh(y)。当且仅当h(y)＝1时，式(32)成立，所以根据h(y)可得p(0)＝p(1)＝0.5。于是序列y中符号0和符号1的概率均等，即符号均匀分布。
[0127]
于是，根据该结论一，任意二进制序列x可以由式(33)给出加权系数，通过加权概率模型无损编码为完全随机的二进制序列y，且二进制序列y也可无损的还原序列x。因序列x已知，所以h(x)确定，则r已知，即r与序列x的熵一一对应。因0≤h(x)≤1，所以r∈[0.5，
1.0)。
[0128]
若仅已知长度为n的二进制序列x(序列x中符号0和符号1均匀分布)，设定r∈[0.5，1.0)通过加权模型译码为长度为n的序列y。显然不同的r可以得出不同熵的序列y。
[0129]
结论二：已知长度为n的二进制序列x中符号均匀分布，且任意给定权系数r∈[0.5，1.0)经加权概率模型译码的结果为二进制序列y，则序列y必然满足：
[0130]
(1)h(y)＜h(x)＝1；(2)序列y的长度为n。
[0131]
结论二的证明过程如下：
[0132]
当二进制序列x已知时，根据结论一，加权系数r与序列y一一对应。由于r已知，所以由式(33)可得：
[0133]
h(y)＝1+log
2 r
ꢀꢀꢀ
(34)
[0134]
若r＝1.0，因为完全随机的二进制序列x有h(x)＝1，由式(33)可得1＝2
h(y)
‑1，则h(y)＝1，所以h(y)＝h(x)。加权概率模型译码过程为等熵变换过程，所以r＜1.0。若0.5≤r＜1.0，
‑
1≤log
2 r＜0代入式(34)，得0≤h(y)＜1。于是h(y)＜h(x)＝1，加权概率模型译码过程是无损降熵变换过程。因加权概率模型是无损编译码过程，且所以译码后的序列y的长度为n。
[0135]
根据结论二，任意二进制序列x中符号满足均匀分布，可以被认为是序列y基于已知权系数r的加权概率模型编码后的结果。使用0.5≤r＜1.0将序列x进行加权概率模型译码时，得到二进制序列y，即0≤h(y)＜1。然后设r＝1.0对随机序列y进行加权编码得到序列z。因为h(y)＜1，所以根据香农无失真定理，序列z的长度必然小于n(可通过香农无失真定理证明)。
[0136]
根据上述结论一和结论二，参照图3，提供第一个实施例，一种基于加权概率模型的无损压缩方法，方法包括以下步骤：
[0137]
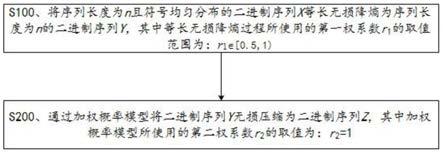
s100、将序列长度为n且符号均匀分布的二进制序列x等长无损降熵为序列长度为n的二进制序列y，其中等长无损降熵过程所使用的第一权系数r1的取值范围为：r1∈[0.5，1.0)。
[0138]
步骤s100的具体实施方式为：
[0139]
s101、设定初始参数：r0＝1，l0＝0，i＝1，j＝0以及r1，r1取区间[0.5，1.0)中的任意值；
[0140]
步骤s101中的参数r1可以[0.5，1.0)区间内任意设置。参数r1的选取决定了本方法的压缩率。
[0141]
s102、根据编码公式l
i
＝l
i
‑1+r
i
‑1f(x
i
‑
1，r1)以及h
i
＝l
i
+r
i
，计算二进制序列x中第i个符号0的区间上标值二进制序列x中第i个符号0的区间上标值其中x
i
表示二进制序列x中的第i个符号，r
i
，l
i
，h
i
为编码参数，p(x
i
)表示第i个符号x
i
的质量概率函数，表示第i个符号x
i
的加权质量概率函数；
[0142]
s103、判断y与的大小，若输出符号0，j＝j+1；若输出符号1；
[0143]
s104、i＝i+1，若j≤n，跳转至步骤s102；若j＞n，得到二进制序列y；
[0144]
s200、通过加权概率模型将二进制序列y无损压缩为二进制序列z，其中加权概率
模型所使用的第二权系数r2的取值为：r2＝1。
[0145]
步骤s200的具体实施方式为：
[0146]
s201、设定初始参数：r0＝1，l0＝0，i＝1，j＝0，v＝0以及r2＝1；
[0147]
为了方便计算和描述，在步骤s201中增加一个参数v，参数v的初始值为0，参数v用于表征加权模型编码后l
i
的值。
[0148]
s202、编码二进制序列y中的第i个符号，若第i个符号为符号0，进入步骤s203；若二进制序列y中的第i个符号为符号1，跳转至步骤s204；
[0149]
s203、根据编码公式r
i
＝r
i
‑1p(x
i
)、l
i
＝l
i
‑1+r
i
‑1f(x
i
‑
1，r2)计算r
i
和l
i
的值，r
i
＝r
i
‑1p(0)，f(
‑
1)＝0，则l
i
＝l
i
‑1；i＝i+1；跳转至步骤s205；
[0150]
s204、根据编码公式r
i
＝r
i
‑1p(x
i
)和l
i
＝l
i
‑1+r
i
‑1f(x
i
‑
1，r2)计算r
i
和l
i
的值，r
i
＝r
i
‑1p(0)，因f(0)＝p(0)，l
i
＝l
i
‑1+r
i
‑1p(0)；
[0151]
s205、若i≤n，则跳转至步骤s202；若i＞n，v＝l
n
，结束编码，输出v，v即为二进制序列z。
[0152]
本实施例提供的一种基于加权概率模型的无损压缩方法，首先序列x基于上述结论二无损降熵为等长的序列y，然后序列y通过加权概率模型(r2＝1)无损压缩为序列z。
[0153]
本实施例提供的基于加权概率模型的无损压缩方法的有益效果在于：
[0154]
根据最大熵定理，均匀分布的二进制序列将无法再进行无损压缩，现有的熵编码均遵从该定理。本方法实施例的核心是提供了一种等长无损降熵变换的过程，因为对均匀分布的二进制序列(对应上述步骤中的二进制序列x)进行了等长无损降熵处理(对应得到的二进制序列y)，所以使得均匀分布的二进制序列可以进行无损压缩。压缩率由式(34)给出，且与自定义的权系数有关。显然本方法的压缩率优于现有的熵编码算法。而且由于本方法是以比特为单位的编译码过程，无需大量的硬件缓存和编码，且可以分段并行处理，所以运算的硬件资源少。本方法可应用的场景主要有：已经压缩过的图像、视频、文件再进行压缩，且压缩比可通过权系数(对应r1)自定义
[0155]
参照图4，基于第一个实施例，本发明的第二个实施例，还提供一种基于加权概率模型的无损解压方法，需要说明的是，本方法是上述第一个实施例提供的基于加权概率模型的无损压缩方法的逆过程，两者是基于同一个发明构思，本基于加权概率模型的无损解压方法包括以下步骤：
[0156]
s300、通过加权概率模型将二进制序列z无损解压为二进制序列y。
[0157]
步骤s300的具体实施方式为：
[0158]
s301、设定初始参数：r0＝1，l0＝0，i＝1，j＝0，v；
[0159]
步骤s301中的参数v均已知，参数v对应第一个实施例的步骤s205中的v。二进制序列z的长度已知。
[0160]
s302、根据编码公式l
i
＝l
i
‑1+r
i
‑1f(z
i
‑
1，r2)以及h
i
＝l
i
+r
i
，计算二进制序列z中第i个符号0的区间上标值二进制序列z中第i个符号0的区间上标值
[0161]
s303、判断v与的大小，若输出符号0，j＝j+1；若输出符号1；
[0162]
s304、i＝i+1；若j小于或等于二进制序列z的序列长度，跳转至步骤s302；若j大于
二进制序列z的序列长度，得到二进制序列y。
[0163]
s400、将二进制序列y等长无损增熵变换成二进制序列x。
[0164]
步骤s400的具体实施方式为：
[0165]
s401、设定初始参数：r0＝1，l0＝0，i＝1，j＝0，v1＝0以及r1；
[0166]
步骤s401的参数r1为已知，参数r1对应第一个实施例中步骤s101中的r1，二进制序列y的序列长度已知，为n。为了方便计算和描述，在步骤s401中增加一个参数v1，参数v1的初始值为0，参数v1用于表征加权模型编码后l
i
的值。
[0167]
s402、编码二进制序列y中的第i个符号，若第i个符号为符号0，进入步骤s403；若二进制序列y中的第i个符号为符号1，跳转至步骤s404；
[0168]
s403、根据编码公式和l
i
＝l
i
‑1+r
i
‑1f(y
i
‑
1，r1)计算r
i
和l
i
的值，f(
‑
1)＝0，则l
i
＝l
i
‑1；i＝i+1；跳转至步骤s405；
[0169]
s404、根据编码公式和l
i
＝l
i
‑1+r
i
‑1f(y
i
‑
1，r1)计算r
i
和l
i
的值，因进入步骤s405；
[0170]
s405、若i≤n，跳转至步骤s402；若i＞n，v1＝l
n
(v1＝x)，结束编码，增熵变换完成。v1即为二进制序列x。
[0171]
本实施例提供的一种基于加权概率模型的无损解压方法是上述第一个实施例方法的逆过程，主要包括：首先序列z解码出序列y；然后序列y通过基于上述结论二无损增熵变换为序列x。
[0172]
本实施例方法是第一个实施例方法的逆过程，本实施例方法与第一个实施例方法是同一个发明构思，此处不赘述其有益效果。
[0173]
参照图5，本发明第三个实施例，提供了一种编码设备，该设备可以是任意类型的智能终端，例如手机、平板电脑、个人计算机等。具体地，该编码设备包括：一个或多个控制处理器和存储器，这里以一个控制处理器为例。控制处理器和存储器可以通过总线或者其他方式连接，这里以通过总线连接为例。
[0174]
存储器作为一种非暂态计算机可读存储介质，可用于存储非暂态软件程序、非暂态性计算机可执行程序以及模块，如本发明实施例中的编码设备对应的程序指令/模块。控制处理器通过运行存储在存储器中的非暂态软件程序、指令以及模块，从而实现上述第一个实施例所述的基于加权概率模型的无损压缩方法和/或第二个实施例所述的基于加权概率模型的无损解压方法。
[0175]
存储器可以包括存储程序区和存储数据区，其中，存储程序区可存储操作系统、至少一个功能所需要的应用程序；存储器可以包括高速随机存取存储器，还可以包括非暂态存储器，例如至少一个磁盘存储器件、闪存器件、或其他非暂态固态存储器件。在一些实施方式中，存储器可选包括相对于控制处理器远程设置的存储器，这些远程存储器可以通过网络连接至该基于编码设备。上述网络的实例包括但不限于互联网、企业内部网、局域网、移动通信网及其组合。
[0176]
所述一个或者多个模块存储在所述存储器中，当被所述一个或者多个控制处理器执行时，执行上述第一个实施例所述的基于加权概率模型的无损压缩方法和/或第二个实
施例所述的基于加权概率模型的无损解压方法。
[0177]
本发明第四个实施例，还提供了一种计算机可读存储介质，所述计算机可读存储介质存储有计算机可执行指令，该计算机可执行指令被一个或多个控制处理器执行上述第一个实施例所述的基于加权概率模型的无损压缩方法和/或第二个实施例所述的基于加权概率模型的无损解压方法。
[0178]
通过以上的实施方式的描述，本领域技术人员可以清楚地了解到各实施方式可借助软件加通用硬件平台的方式来实现。本领域技术人员可以理解实现上述实施例方法中的全部或部分流程是可以通过计算机程序来指令相关的硬件来完成，程序可存储于计算机可读取存储介质中，该程序在执行时，可包括如上述方法的实施例的流程。其中，所述的存储介质可为磁碟、光盘、只读存储记忆体(read only memory，rom)或随机存储记忆体(random access memory，ram)等。
[0179]
在本说明书的描述中，参考术语“一个实施例”、“一些实施例”、“示意性实施例”、“示例”、“具体示例”、或“一些示例”等的描述意指结合该实施例或示例描述的具体特征、结构、材料或者特点包含于本发明的至少一个实施例或示例中。在本说明书中，对上述术语的示意性表述不一定指的是相同的实施例或示例。而且，描述的具体特征、结构、材料或者特点可以在任何的一个或多个实施例或示例中以合适的方式结合。
[0180]
尽管已经示出和描述了本发明的实施例，本领域的普通技术人员可以理解：在不脱离本发明的原理和宗旨的情况下可以对这些实施例进行多种变化、修改、替换和变型，本发明的范围由权利要求及其等同物限定。