一种时序数据库的数据压缩方法及系统与流程

1.本发明涉及一种压缩方法及系统，具体涉及一种时序数据库内的数据压缩方法及系统，属于计算机技术领域。


背景技术：

2.时序数据，即时间序列数据，我们把按照时间戳的大小顺序排列的一系列记录值的数据称为时间序列数据(time series data)。在日常生活中，时序数据相当常见，比如，汽车的位置定位，在一段时间内某辆特定汽车的其他属性，包括型号、颜色、车牌号、所有者等都是不变的，但它的位置数据是随着时间变化不断在变化的，那么根据时间确定的位置值及其他属性所组成的一系列数据就是一组时序数据，当我们驾驶汽车开启导航时，就需要根据这一组时序数据判断接下来到达目的地的路线以及存储驾驶记录，在即将到来的无人驾驶中更是必不可少的。在互联网中，时序数据更是无处不在，比如，用户访问网站的记录、应用系统的系统日志数据等等。
3.时序数据随时间不间断的增长，且增长频率越来越快。在一些比较热点的场景下，数据积累的速度将会十分惊人。因此数据库中将要存储海量的时序数据。这些过往的数据的存在不仅占据着相当大一部分的存储空间，而且查询利用率特别低，甚至更多情况下用户仅需要近似值，同时还消耗着数据库相当大一部分资源。因此有必要对这些数据进行进一步的压缩，以减少资源的消耗，而实际上，目前的开源时序数据库也确实是这样做的，但其中的压缩算法效率较低。


技术实现要素：

4.本发明为了解决时序数据库中压缩算法效率低的问题，进而提出了一种时序数据库的数据压缩方法及系统。
5.本发明采取的技术方案是：
6.一种时序数据库的数据压缩方法，它包括以下步骤：
7.s1、利用时序数据库的压缩算法提取原始时序数据，原始时序数据包括整型数据和浮点数据；
8.s2、计算s1提取的整型数据的delta数组；
9.s3、建立回归模型，设置回归模型中误差损失函数的权重因子为10，将s2中得到的delta数组输入回归模型内进行训练，输出整型数据数值的预测值，直到loss收敛，得到训练好的回归模型；
10.s4、将s2中得到的delta数组输入s3中训练好的回归模型内，得到整型数据数值的预测值；
11.s5、将s4中得到的整型数据数值的预测值与s1原始时序数据中整型数据数值的真实值作差，得到误差结果；
12.s6、对s5中得到的误差结果采用zigzag变换方法进行变换，得到变换后的误差结
果，利用哈夫曼编码将变换后的误差结果进行保存；
13.s7、对s1中提取的浮点数据进行精度缩减，将精度缩减后的浮点数据采用异或运算进行压缩。
14.优选的，所述s1中利用时序数据库的压缩算法提取原始时序数据，原始时序数据包括整型数据和浮点数据，具体过程为：
15.当时序数据库后台进程处于每秒处理数据量小于20万条或休息时，根据设置的时间段或时序数据库默认的时间段利用时序数据库的压缩算法提取原始时序数据，所述原始时序数据包括整型数据和浮点数据。
16.优选的，所述设置的时间段为用户在查询时根据需要自己指定的时间段。
17.优选的，所述设置的时间段为七天或24小时。
18.优选的，所述时序数据库默认的时间段为七天。
19.优选的，所述s3中建立的回归模型包括多项式回归模型、正弦回归模型。
20.优选的，所述s3中设置回归模型中误差损失函数的权重因子为10，则回归模型的输出结果需同时满足以下条件：
21.条件一：所有误差代价之和的10倍小于所有误差收益之和；
22.条件二：本次迭代的整体代价小于上一轮迭代的整体代价。
23.优选的，所有误差代价之和为负值误差绝对值之和；所有误差收益之和为正值误差之和；整体代价为所有误差的绝对值之和。
24.优选的，所述s7中对s1中提取的浮点数据进行精度缩减，将精度缩减后的浮点数据采用异或运算进行压缩，具体过程为：
25.根据s1中得到的浮点数据，选取浮点数据尾数部分中除前4位之外的后19位数据进行精度缩减，即若选取的19位数据的第1位为1，则所述前四4位进1，否则不进1，并将后19位数据置0，将精度缩减后的浮点数据采用异或运算进行压缩。
26.一种时序数据库的数据压缩系统，包括存储器、处理器以及存储在所述存储器中并可在所述处理器上运行的计算机程序，所述处理器执行所述计算机程序时实现如一种时序数据库的数据压缩方法的任一步骤。
27.有益效果：
28.本发明将时序数据分为整型数据和浮点数据，针对整型数据和浮点数据分别采用不同的压缩方法进行压缩，使整型数据和浮点数据的压缩效果均达到最佳，有效的提高了时序数据库中压缩算法的效率。对于整型数据，本发明通过建立回归模型对其进行压缩，使时序数据库在存储时只需要存储整型数据中与回归模型参数相同的数据作为回归模型的输入，输出整型数据的数值预测值，在得到整型数据的数值预测值后与整型数据的数值真实值作差，即可得到二者的误差，在对误差进行zigzag变换，将变换后的误差利用哈夫曼编码的方式进行存储，至此，即完成了原始时序数据整型数据的压缩处理，同时满足了无损压缩。这样在计算某个时间结点的数据时，仅将存储的参数输入回归模型内，就可以获取时序数据库内存储的对应的数据，相当于在回归模型内进行了一次简单的数学公式计算，使回归模型轻量化，不仅提高了时序数据整型数据的压缩效率，还极大的提升了查询时间，以满足用户的查询需求，同时相比于传统的将原始数据进行变换格式并存储要节省极大的存储空间。对于浮点数据，首先对其进行精度缩减，将时序数据库中浮点类型数据之间的差异集
中在浮点数据尾数部分的前4位。将缩减处理后的浮点数据使用异或运算进行压缩，如此能够减少大多数尾数部分占用的存储空间，尽可能得到相似的浮点数据二进制表示形式，可以相当大的提高浮点数据的压缩比，从而提高时序数据浮点数据的压缩效率。
附图说明
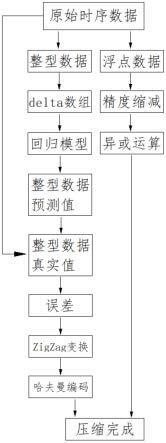
29.图1是本发明的结构流程图；
具体实施方式
30.具体实施方式一：结合图1说明本实施方式，本实施方式所述一种时序数据库的数据压缩方法，它包括以下步骤：
31.s1、利用时序数据库的压缩算法提取原始时序数据，原始时序数据包括整型数据和浮点数据，具体过程为：
32.当时序数据库后台进程处于每秒处理数据量≤20万条或休息状态时，根据设置的时间段或时序数据库默认的时间段利用时序数据库本身自带的数据压缩算法提取原始时序数据，所述原始时序数据例如汽车位置定位时，根据时间确定的位置值及其他属性所组成的一系列数据，并将原始时序数据分为整型数据和浮点数据。所述设置的时间段为用户在查询时根据需要自己指定的时间段，一般为七天或24小时；所述时序数据库默认的时间段为七天。为了保证数据的压缩效率，针对整型数据和浮点数据分别采用不同的压缩方法进行压缩，使整型数据和浮点数据的压缩效果均达到最佳。
33.s2、计算s1提取的整型数据的delta数组；
34.根据s1中得到的整型数据，计算其delta数组，delta数组能够提高压缩的效果。
35.s3、建立回归模型，设置回归模型中误差损失函数的权重因子为10，将s2中得到的delta数组输入回归模型内进行训练，输出整型数据数值的预测值，得到训练好的回归模型；
36.由于回归模型重要的基础或者方法是回归分析，而回归分析最主要就是使用曲线/线拟合若干的数据点，由此保证从曲线或线到数据点的距离差异最小，有利于帮助数据分析或研究人员排除并估计出一组最佳的变量。所以本发明采用回归模型对时序数据进行预测分析。
37.首先，建立回归模型，设置回归模型中误差损失函数的权重因子为10，模型训练过程为多轮迭代。定义每一轮迭代的收益为正值误差之和，代价为负值误差绝对值之和，整体代价为收益和代价之和，即所有误差绝对值之和。
38.将s2中得到的delta数组输入回归模型内进行训练，训练至输出结果同时满足以下两个条件，即可得到训练好的回归模型，条件一：所有误差代价之和的10倍小于所有误差收益之和；条件二：本次迭代的整体代价小于上一轮迭代的整体代价；举例如下：
39.例子1：假设某一轮迭代后的误差数据依次为-10、-30、12、-18、25、96，那么本次的误差收益为12+25+96＝133，代价为10+30+18＝58，则133《58*10，即误差收益小于误差代价的10倍，不满足条件一，进入下一轮迭代。每一轮迭代是将s2中得到的所有delta数组输入回归模型内进行训练。
40.例子2：假设上一轮的整体代价为80，本次迭代后的误差数据依次为-1、-3、12、-8、
25、96，那么本次的误差收益为12+25+96＝133，代价为1+3+8＝12，则133≥12*10，即误差代价的10倍小于误差收益，满足条件一；但上一轮的整体代价小于本次的整体代价，即133+12＝145》80，不满足条件二，则进入下一轮迭代。
41.例子3：假设上一轮整体代价为150，本次迭代后的误差数据依次为-1、-3、12、-8、25、96，那么本次预测的误差收益为12+25+96＝133，代价为1+3+8＝12，则133≥12*10，即误差代价的10倍小于误差收益，满足条件一；此时本次的整体代价小于上一轮迭代的整体代价，即145《150，满足条件二；所以本次迭代同时满足条件一和条件二，则输出本轮迭代结果，得到训练好的回归模型。
42.回归模型包括多项式回归模型、正弦回归模型等，利用计算好的delta数组分别输入多项式回归模型和正弦回归模型内进行数据拟合训练，根据得到的输出结果，选取其中的最优结果作为输出，将所述输出最优结果对应的模型作为最优回归模型，使之为训练好的回归模型。
43.本发明通过设置回归模型对原始时序数据(例如汽车位置定位时，根据时间确定的位置值及其他属性所组成的一系列数据)整型数据进行压缩，使时序数据库在存储时只需要存储回归模型的参数，这样在计算某个时间结点的数据时，仅将存储的参数输入回归模型内，就可以获取时序数据库内存储的对应的数据，相当于在回归模型内进行了一次简单的数学公式计算，使回归模型轻量化，且极大的提升了查询时间，以满足用户的查询需求。同时相比于传统的将原始数据进行变换格式并存储要节省极大的存储空间。
44.轻量化的回归模型具有以下优点：
45.(1)只需要保存原始时序数据(例如汽车位置定位时，根据时间确定的位置值及其他属性所组成的一系列数据)中整型数据少量的参数便可以表示一段时序数据。
46.(2)根据原始时序数据(例如汽车位置定位时，根据时间确定的位置值及其他属性所组成的一系列数据)整型数据进行训练回归模型的过程十分快速，不会消耗过多的资源。
47.(3)在进行数据解压即进行回归模型预测时，计算速度快，足以满足用户需求。
48.s4、将s2中得到的delta数组输入s3中训练好的回归模型内，得到整型数据数值的预测值；
49.此步骤得到的整型数据数值的预测值便于后续与整型数据数值的真实值作比较，得到二者的误差，从而实现数据的压缩。
50.s5、将s4中得到的整型数据数值的预测值与s1原始时序数据中整型数据数值的真实值作差，得到误差结果；
51.在得到原始时序数据(例如汽车位置定位时，根据时间确定的位置值及其他属性所组成的一系列数据)时，即可直观的得到整型数据数值的真实值，将整型数据数值的预测值与整型数据数值的真实值作差，得到二者的误差，在对误差进行处理。
52.s6、对s5中得到的误差结果采用zigzag变换方法进行变换，得到变换后的误差结果，利用哈夫曼编码将变换后的误差结果进行保存；
53.采用zigzag变换方法对s5中得到的误差结果进行处理，由于zigzag变换具有高效压缩前导0的特性，所以可以使误差尽可能的多为正值，以便于更好的利用zigzag特性，但同时又不能为了保证误差为正值而矫枉过正，所以本发明使用上述权重因子进行权衡，再对处理后的误差进行保存，至此，即完成了原始时序数据(例如汽车位置定位时，根据时间
确定的位置值及其他属性所组成的一系列数据)整型数据的压缩处理，同时满足了无损压缩。
54.s7、对s1中提取的浮点数据进行精度缩减，将精度缩减后的浮点数据采用异或运算进行压缩，具体过程为：
55.根据s1中得到的浮点数据，选取浮点数据尾数部分中除前4位之外的后19位数据进行精度缩减，具体过程为：若选取的19位数据的第1位为1，则所述前4位(即尾数部分中除前4位)进1，否则不进1，并将后19位数据置0；
56.将精度缩减后的浮点数据采用异或运算进行压缩。
57.此步骤是将s1中得到的浮点数据进行有损压缩。首先，对浮点数据进行精度缩减，即选取浮点数据的尾数部分(共23位)除前4位之外的后19位数据，若选取的19位数据的第1位为1，则所述前四位进1，否则不进1，并将后19位数据置0。经过上述缩减处理后可将时序数据库中浮点类型数据之间的差异集中在浮点数据尾数部分的前4位。再将缩减处理后的浮点数据使用异或运算进行压缩，如此能够减少大多数尾数部分占用的存储空间，尽可能得到相似的浮点数据的二进制表示形式，可以相当大的提高浮点数据的压缩比，至此，即完成了原始时序数据(例如汽车位置定位时，根据时间确定的位置值及其他属性所组成的一系列数据)浮点数据的压缩处理。
58.具体实施方式二：结合图1说明本实施方式，本实施方式所述一种时序数据库的数据压缩系统，包括存储器、处理器以及存储在所述存储器中并可在所述处理器上运行的计算机程序，所述处理器执行所述计算机程序时实现如一种时序数据库的数据压缩方法的任一步骤。