图像/视频的变换域中基于上下文的建模方法及其系统与流程

本发明涉及的是一种图像/视频编码解码及其他处理技术领域的方法及系统，具体是一种刻画自然图像在某一变换域(如离散余弦变换(DCT)域)中各向异性相关性的二维马尔可夫随机场(Markovrandomfield)的建模方法及其系统。

背景技术：
目前的图像/视频处理技术，如压缩、重构、增强、分析等，大多是在变换域进行的。常用的变换域有离散余弦变换(DCT)，离散傅立叶变换(DFT)，哈达码变换等。变换的作用是将图像/视频信号中的能量集中于少数变换系数之中，从而显著地减小信号中的统计冗余。学术界对该过程有多种描述：如能量打包(energypacking)、去相关或图像/视频信号的稀疏表示等。但即使在变换域中，自然图像/视频信号也远非独立同分布(i.i.d)，而应该被归类于马尔可夫随机过程(Markovrandomprocesses)。因此，对于图像/视频信号在变换域中的上下文统计建模成为被广泛应用的图像/视频处理系统中的关键组成部分。这里所谓的上下文统计建模是指马尔可夫或近似马尔可夫信号的条件概率的估计方法或过程。在基于变换的图像/视频压缩系统，如MPEG、JPEG、JPEG2000、H.264中，图像/视频信号的上下文统计建模无疑对系统的率失真(rate-distortion)性能至关重要，其作用是预测用于驱动熵编码器(如基于上下文的算术编码器等)的变换系数的条件概率。在熵编码过程中，任何对于条件概率的预测偏差都会直接导致编码性能的下降。准确地说，与理论最短码长比，预测概率偏差所造成的冗余码长等于其与真实概率分布之间的互信息熵(relativeentropy)，或者KL距离(Kullback-Leiblerdistance)。因此上下文统计建模的精度最终决定了系统的压缩性能。现有的上下文建模方法往往利用自然图像具有快速下降的功率谱的特性(文献中假设为指数下降)。但具有快速下降的功率谱本身无法表征图像/视频信号在变换域中的统计特性，这是因为图像和视频的信号能量在频域上仅为一维分布，而在变换域中则为二维或者三维。尤其如边界，纹理等含有方向性的图像具有在二维的变换域里通过其变换系数体现出二维方向相关性的特点，上述变换系数的方向相关性在对含有边界的图像像素块进行二维离散变换时尤为显著，对于含有边界或者规则纹理的图像块，信号能量被集中于方向子带中，如图1(a)和1(c)所示即为包含不同朝向边界的图像像素块进行离散余弦变换(DCT)的结果。对于包含平滑阴影的像素块，其信号能量则集中于低频区域，而DCT变换系数以辐射状并且近乎相同的速度衰减，如图1(b)所示。可见自然图像在离散余弦变换(DCT)域中可以近似为同时具有径向(radialdirection)和逆径向(anti-radialdirection)相关性的二维马尔可夫随机场模型。通过上述分析揭示了多种现行国际图像视频压缩标准，如JPEG、MPEG及H.264等所采用的常见的DCT系数之字形(Zigzag)扫描方法从本质上具有缺陷。Zigzag扫描为逆径向(anti-radialdirection)往复式扫描，彻底忽略自然图像在径向上所具有的统计相关性。事实上，MPEG和H.264标准为了弥补该缺陷，分别提出水平和垂直方向的扫描模式作为Zigzag扫描方式的代替。但多扫描模式的切换仅为局部且不灵活的临时方案，无法对图像/视频信号在变换域中的任意方向相关性进行建模，并且对扫描模式的编码也会造成额外的码率开销。经过对现有技术的检索发现，中国专利文献号CN1741616，公开日2006-03-01，记载了一种基于上下文的自适应熵编码方法，该技术包括以下步骤：编码时：扫描当前变换块中已被量化的DCT系数，由此形成(level，run)数对序列;然后按扫描的逆向顺序对数对序列中每一数对进行熵编码，在编码中，利用已被编码块中已完成编码的数对的值动态自适应构造上下文统计模型，同时，也提出一个上下文模型加权融合技术来进一步提高模型的压缩性能;用上一步骤所获得的上下文统计模型来驱动熵编码。基于上下文的自适应熵解码方法是编码方法的逆。但该技术具有以下的缺陷和不足：虽然该方法采用游程(run-length)的方式对两个非0系数之间连续的0系数进行了组合编码，但该方法并未对其他的典型系数组合进行合并，并且依然未能跳出Zigzag的简单扫描方式。中国专利文献号CN1431828，公开日2003-07-23，记载了一种“用于编码/解码图像信号的最佳扫描方法”，该技术在一种通过离散余弦变换编码图像信号的方法中，在多个参考块中至少一个被选择。产生一个扫描顺序，其中进行扫描参考块的要编码的块，并且以所产生的扫描顺序扫描要编码的块。所述至少一个被选择的参考块与要编码的块在时间或空间上邻近。当扫描要编码的块的时候，从所述至少一个所选择的参考块获得发生非零系数的概率，并且从最高的概率开始以降序确定扫描顺序。在此，如果概率相同，则扫描顺序被产生为一个之字形的扫描顺序。但该方法依然未能从根本上解决Zigzag扫描模式的弊端，并且其对变换系数的自适应扫描依然是针对单个系数来进行的，并未对拥有近似性质的系数块进行合并，因此，该方法的编码效率依然不足以令人满意。

技术实现要素：
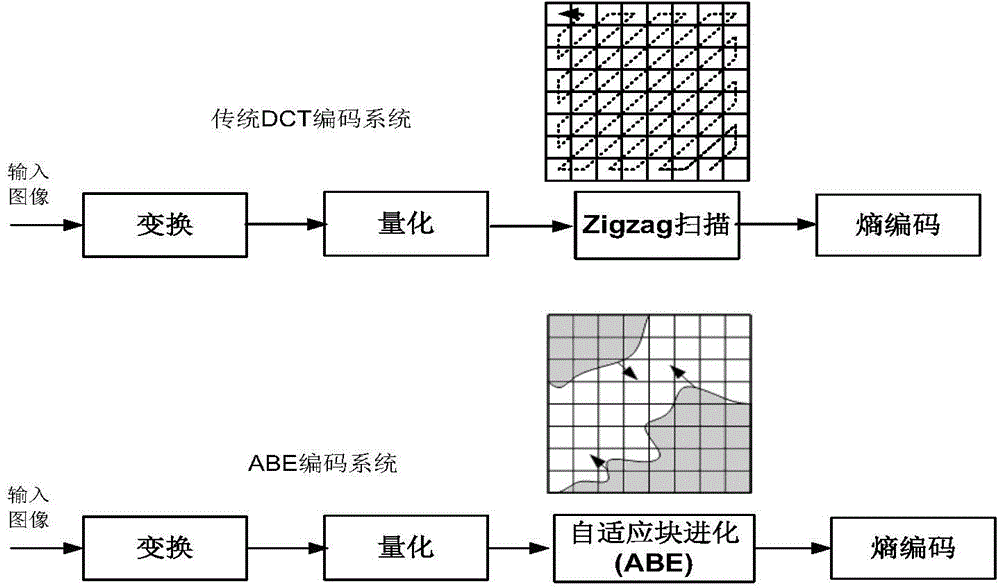
本发明针对现有技术存在的上述不足，提供一种图像/视频的变换域中基于上下文的建模方法及其系统，通过自适应块进化法(ABE：AdaptiveBlockEvolution)，与现有锯齿式(Zigzag)、水平或垂直的扫描方式不同，该方法并不采用固定的一维扫描顺序，而是采用自适应二维扫描方式，对变换域系数同时从径向和逆径向的相关性进行统计建模。本发明除了能够作为图像视频压缩中的有效工具以外，还能够用于执行去噪、插值、分类、视觉信息检索及提取、数字水印、信息隐藏、图像检索、隐写分析等其他图像/视频处理应用中。本发明是通过以下技术方案实现的：本发明涉及一种变换域里上下文统计建模方法，通过自适应地构建一个二维马尔可夫模型以反应图像/视频信号在二维变化域里的方向相关性，该方法具体包括：将多个或单个变换系数组成二维马尔可夫过程中的状态；在线或离线地计算两个相邻马尔可夫状态之间的传递概率；从初始状态起，通过传递概率分别实现单个或多个遍历方向的自适应。所述的变换系数可以经过量化或未经过量化；所述的二维马尔可夫过程中的状态是指变换域中的一个或一组相邻且相关的系数，该状态通过典型模式的系数块进行定义；所述的初始状态是指：以最低频率系数和/或最高频率系数为参照点，聚集在一起的具有相同或相近数值且相近频率的系数群所构成的系数块；该系数群的洲际即为广义半径。所述的传递概率P(si|si-1)专指二维马尔可夫过程中的传递概率，可通过离线或者在线的方式计算得到，其中：si为下一状态，si-1为当前状态，i表示当前遍历的变换系数的系数块的序号，其取值为1至二维马尔可夫过程中的状态总数。所述的遍历方向的自适应是指：根据当前状态和其所有下一个可能状态之间的传递概率中的最高值所对应的状态来选择下一个状态；对于两个以上的初始状态则分别进行上述自适应计算。本发明涉及一种基于变换域上下文统计建模的图像/视频压缩方法，包括以下步骤：第一步、对于输入图像进行系数变换；第二步、对变换系数进行基于上下文的建模并确定初始状态s0；第三步、在线或离线地以二维马尔科夫过程对状态si-1下的所有可能传递概率P(si|si-1)进行计算和比较，并基于其中的最优值作为下一个状态si；第四步、对第三步得到的下一个状态si，用其对应的传递概率P(si|si-1)驱动熵编码器，输出状态si所对应的变化系数的输出码，然后返回第三步根据新的状态重新进行计算和比较，直至遍历完所有变换系数并得到所有输出码组成的完整码流。所述的初始状态采用广义半径的方式编码最低频域里至少一个值为1的系数或系数块和/或最高频域里的至少一个值为0的系数或系数块和/或频域任意部分中具有明显特征的系数块。所述的明显特征是指：两个以上毗邻且具有相同值或呈典型分布的系数对或系数块。本发明涉及一种基于变换域上下文统计建模的图像/视频压缩系统，包括：变换模块、自适应块进化(ABE)模块和熵编码模块，其中：变换模块，对图像进行系数变换；ABE模块，对变换模块输出的变换系数进行基于上下文的建模，并按照自适应方式逐步将遍历过程中每一步得到的传递概率依次输出至并驱动熵编码模块。熵编码模块，根据ABE模块输出的传递概率对变换系数进行熵编码并输出。所述的基于上下文的建模是指：将变换域中的一个或一组相邻且相关的系数作为二维马尔科夫过程的状态，以最低频率系数和/或最高频率系数为参照点，聚集在一起的具有相同或相近数值且相近频率的系数群所构成的系数块作为模型的初始状态。所述的自适应方式是指：从基于上下文的模型的初始状态起，计算其所有下一个可能状态之间的传递概率中的最高值所对应的状态作为下一个状态。本发明与现有H.264压缩方式相比提高了编码效率，尤其当码率升高至0.45或以上时，ABE编码系统的码流长度可减少至接近90%。附图说明图1为实施例1中不同图像的16x16大小像素块对应DCT变换系数示意图(系数幅值通过明暗程度示意)。图2为传统DCT编码系统和本发明的ABE编码系统的对比。图3为马尔科夫状态下的8x8大小多个DCT变换系数块示意图，具体如图中灰色区域。图4为以高传递概率为方向进行状态变换的示意图，第i步至第iv步；图中：(a)为径向状态变化；(b)为水平状态变化。图5为变换域的一维或二维方向横断扫描示意图；图中：(a)为从低变换域作为初始状态进行遍历；(b)为从高变换域作为初始状态进行遍历；(c)为分别从低变换域和高变换域同时进行遍历。图6为验证本发明编码性能的测试实验所用图像集。图7为本发明编码性能与现存最好编码系统H.264的对比结果。具体实施方式下面对本发明的实施例作详细说明，本实施例在以本发明技术方案为前提下进行实施，给出了详细的实施方式和具体的操作过程，但本发明的保护范围不限于下述的实施例。实施例1二维马尔科夫建模为进一步体现出本发明ABE方式的创新性，下面以众多图像视频压缩标准和系统中最为核心的处理过程，即量化后的二维DCT系数的熵编码为例。传统的DCT编码系统与本发明ABE编码系统框图如图2所示。与传统DCT编码系统类似，ABE系统也首先输入图像进行DCT变换及量化，但与传统系统所采用的锯齿扫描(Zigzag)不同，ABE系统采用更为灵活的自适应块进化方法，从而拥有更高的编码效率。经量化后，大部分非显著DCT系数被量化为0，而剩下的非0，即显著系数，往往会沿某方向集聚。相反大量的非显著系数(0)，则会沿着从低频到高频的方向扇形扩散。为提高压缩效率，ABE方法采用有序二维马尔可夫模型以及相邻像素块序号分解0和非0的位置(比如：生成权重图)。在上述二维马尔可夫建模过程将对当前状态si-1到下一个状态si的传递概率P(si|si-1)进行预测。所述的状态是指变换域中的一组相邻且相关的系数块。比如一组位于最高频域的全0系数块构成一个状态(如图4(a))；而另一组位于最低频域的全非0系数块则构成另一个状态(如图4(b))。更普遍地，一个状态则由部分0系数和非0系数随意地构成(如图3(c))。作为对量化后的变换域DCT系数进行熵编码，ABE方法通过si-1→si方式的变换以提高传递概率P(si|si-1)，实现横贯变换域的方式进行扫描。变换过程中的初始状态s0可能是一个位于高频域且包含0的大系数块，或者是一个位于低频域且包含非0的大系数块，分别如图4(b)和图4(a)所示。这些全0或全1的初始状态能够方便地通过一整数数值的广义半径实现编码，该广义半径的方法较块尾(EOB)方法更为有效且广泛应用于现有压缩标准中。二维变换域的横贯式扫描过程中的中间状态由位于当前扫描区域首部的连续的0系数或非0系数组成。通过对相邻状态的变换进行上下文统计建模，ABE方法实现对变换域的特殊方向(大部分为径向)上相关性的利用。由于变换系数的方向性与图像块中的方向特征紧密相关，当两个相邻的状态si和si-1是同一类型并且方向相同时，其传递概率P(si|si-1)将表现得更高。通过利用该规律，ABE方法可以在横贯式扫描过程中或压缩变换系数时实现自适应的方向状态变换，如图4所示。对变换系数进行遍历的推进方向可以是单向的：从高频到低频或者从低频到高频，但也可以是双向的，即从高频和低频分别向中频推进最终汇合。图5是这三种遍历方式的示意。通过合理地选择马尔可夫状态并实施高概率变换，ABE方法可以与基于上下文的匹配熵编码器相结合，以更短的码长对变换系数进行编码。实施例2图像压缩应用本实施例包括以下步骤：第一步、对于输入图像进行系数变换；所述的系数变换可采用DCT变换或KLT(Karhunen－Loeve)变换，或采用现有已知其他变换方法与以下遍历方式进行组合，经实验核实均可以达到与本实施例及图7中所示相近似的效果。所述的系数变换还可以附加量化处理；第二步、对变换系数进行基于上下文的建模并确定初始状态s0；本实施例中的初始状态采用广义半径的方式编码，该初始状态可以是以下任意一种：i)聚集于最低频域的若干数值为1的系数块，如图5(a)所示；ii)聚集于最高频域的若干数值为0的系数块，如图5(b)所示；iii)上述i)和ii)的组合，如图5(c)所示。第三步、在线或离线地以二维马尔科夫过程对当前状态si-1的所有可能传递概率P(si|si-1)进行计算和比较，并基于其中的最大值作为下一个状态si。第四步、对第三步得到的下一个状态si，用传递概率P(si|si-1)去驱动熵编码器，输出状态si所对应的变化系数的输出码，然后返回第三步根据新的状态重新进行计算和比较，直至遍历完所有变换系数并得到所有输出码组成的完整码流。上述步骤中i为1至二维马尔可夫过程中的状态总数；如初始状态的个数多于1个，则可以采用如图5(c)的方式实现两个以上方向上的同时遍历以提高编码速度。在本应用中，涉及上述方法的实现系统，包括：变换模块、自适应块进化(ABE)模块和熵编码模块，其中：变换模块，对图像进行如DCT或KLT的系数变换；ABE模块，对变换模块输出的变换系数进行基于上下文的建模，并按照自适应方式逐步选择最高转移概率P(si|si-1)对应状态进行马尔科夫过程的跳转，最终遍历所有系数，同时在遍历过程中将P(si|si-1)依次输出至熵编码模块以驱动熵编码器。熵编码模块，根据ABE模块逐步输出的传递概率对变换系数进行熵编码并输出。所述的变换模块可附带有量化处理功能；所述的基于上下文的建模是指：将变换域中的一个或一组相邻且相关的系数作为二维马尔科夫过程的状态，以最低频率系数和/或最高频率系数为参照点，聚集在一起的具有相同或相近数值且相近频率的系数群所构成的系数块作为模型的初始状态。所述的自适应方式是指：从基于上下文的模型的初始状态起，计算其所有下一个可能状态之间的传递概率，并基于其中的最高值选择下一个状态。本实施例采用如图6所示的38幅常用测试图像来验证实施实例1所述ABE系统的编码性能。每幅图像首先经过8x8的DCT变换，然后采用不同的量化步长分别对DCT系数的显著图(significantmap)进行编码。作为比较，我们选用当前效果最好的H.264编码器，来对相同的显著图来进行编码，为了客观比较两种方法，熵编码模块均采用H.264编码器默认的自适应二元算术编码器CABAC。并且，所有上下文的初始概率都设置为0.5。需要说明的是，在本实例中，ABE编码系统采用的上下文（context）数目是H.264的三倍(378vs126），所以ABE系统的上下文稀释（contextdilution）惩罚更为严重。因此，该初始化设置方式其实更有利于H.264编码系统。我们比较两种编码方式最终所生成码流长度的相对比值：γ＝(L264-LABE)/L264，其中，LABE表示ABE编码系统生成的码流长度，L264表示H.264系统生成的码流长度。不同图像的在不同码率下的γ如图7所示，从图中可以看出，与H.264相比，ABE编码系统明显更为高效，尤其当码率升高时，ABE编码系统的优势更为明显。此外，经测试表明，ABE系统对其他系数变换，如KLT变换等，以及采用其他现存熵编码器，如JPEG2000所采用的MQ编码器，以及霍夫曼编码器等，都可达到类似于图7的性能提升。