一种离散动态系统时延特性的测定方法与流程

本发明涉及工业控制领域，具体是涉及一种离散动态系统时延特性的测定方法。
背景技术：
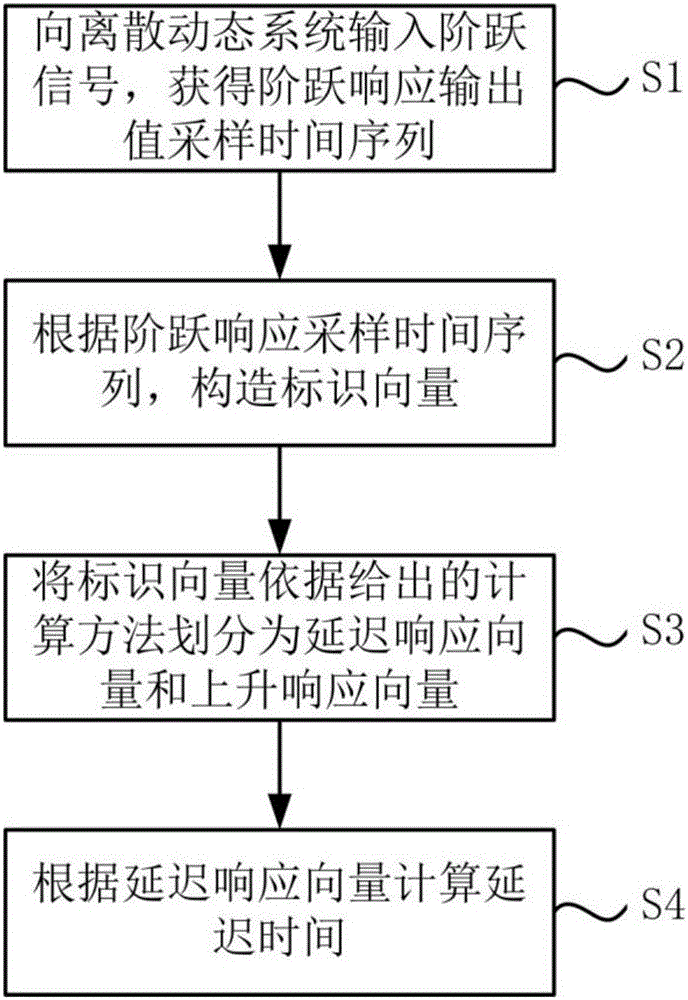
：工业过程中的物理系统带有不可避免的时延特性，即外界对物理系统的输入需要经过延迟时间τ之后才能真正地作用于物理系统。如图1中离散动态系统阶跃输入的响应序列所示，延迟时间τ与时间常数t的区别在于：延迟时间τ指从外界输入施加到真正作用于物理系统的时间，时间常数t则是指从外界输入作用于物理系统到输出有显著变化的时间。具有时延特性的工业过程包括：如履带传输、管路输送、物料成分测定和锅炉换热等，以及具有非实时任务调度性质的机电一体化系统。在大多数工业过程中，延迟时间τ远小于时间常数t，因此延迟时间τ通常被忽略不计。但是当延迟时间τ超过时间常数t的30％时，忽略不计延迟时间τ将对控制系统的性能产生显著影响，甚至导致控制系统不稳定。因此，对具有时延特性的工业过程通常采用基于特定算法的控制系统设计方法，这些方法均需要准确、定量地确定延迟时间τ。另外，对于离散动态系统，其系统采样时间主要根据延迟时间τ和时间常数t确定。目前对于离散动态系统延迟时间τ的通常根据最大上升斜率切线确定。如附图1所示，沿响应序列最大上升斜率的方向做切线，该切线与时间轴相交，该相交点与阶跃输入的开始时刻的时间区间为延迟时间τ。以上方法的缺点是对测量中的噪声的抗干扰能力较差，导致测量结果的准确性和重复性较差。技术实现要素：针对现有技术中存在的缺陷，本发明的目的在于提供一种离散动态系统时延特性的测定方法，能够克服测量噪声的干扰，准确测定延迟时间，计算结果重复性好。为达到以上目的，本发明采取的技术方案是：一种离散动态系统时延特性的测定方法，包括以下步骤：S1.向所述离散动态系统输入阶跃信号，获得所述离散动态系统的阶跃响应输出值，所述阶跃响应输出值为采样时间序列yi，i＝1,2,…,N，其中，i为采样点的序号，yi为第i个采样点的值，N为采样点总数，且T为总采样时间，TS为采样周期；S2.根据所述阶跃响应采样时间序列yi，构造标识向量；S3.将所述标识向量依据给出的计算方法划分为延迟响应向量和上升响应向量，所述延迟响应向量包含所述标识向量中的前N1个元素，所述上升响应向量包含所述标识向量中的后N-N1-1个元素，其中，1≤N1≤N-1；S4.根据所述延迟响应向量计算延迟时间。在上述技术方案的基础上，步骤S2具体包括：S2.1根据所述阶跃响应采样时间序列yi构造数据矩阵Z：Z=y1y2...yN-1y2y3...yN2×(N-1),]]>其中，数据矩阵Z的下标2×(N-1)表示该矩阵为2行N-1列的矩阵；对所述数据矩阵Z进行奇异值分解：Z＝Q2×2G2×2V2×(N-1)，其中，Q为正交矩阵，G为对角矩阵，V为行正交矩阵；S2.2根据矩阵V，构造关系矩阵M：H=V(N-1)×2T×V2×(N-1),]]>其中，M为N-1行N-1列的矩阵，VT为V的转置矩阵；对所述关系矩阵M进行奇异值分解：M=W(N-1)×2Σ2×2W2×(N-1)T,]]>其中，Σ为对角矩阵，WT为W的转置矩阵，W为列正交矩阵，W=w11w12w21w22......w(N-1)1w(N-1)2(N-1)×2;]]>S2.3截取W矩阵的后K行构造子矩阵X：X=w(N-K+1)1w(N-K+1)2w(N-K+2)1w(N-K+2)2......w(N-1)1w(N-1)2K×2,]]>其中，2≤K≤N-1；计算加权向量δ：δ=(X2×KTXK×2)-1X2×KT1K×1,]]>其中，XT为X的转置矩阵，XTX为两个矩阵XT和X相乘得到的矩阵，(XTX)-1为两个矩阵XT和X相乘得到的矩阵XTX的逆矩阵，1K×1为列向量，1K×1中的元素个数为K，并且所有元素的值均为1，δ为2行1列矩阵，即列向量；S2.4计算所述标识向量L：L＝W(N-1)×2×δ2×1，其中，所述标识向量L为N-1行1列矩阵，即列向量。在上述技术方案的基础上，步骤S3具体包括：S3.1将所述标识向量L依据给出的计算方法划分为延迟响应向量和上升响应向量，其中，先将所述延迟响应向量Sf的元素个数n设为1，其中，n＝1,2,…,N-1，则所述上升响应向量Sb的元素个数为N-n-1＝N-2；所述延迟响应向量Sf包含所述标识向量L的前n个元素lj，lj为所述标识向量L的第j个元素，j＝1,2,…,N-1，所述上升响应向量Sb包含所述标识向量L的后N-n-1个元素lj；S3.2分别计算从S3.1中获得的所述延迟响应向量Sf和上升响应向量Sb中所有元素的平均值：cf(n)=1nΣlj∈Sflj,]]>cb(n)=1N-n-1Σlj∈Sblj,]]>其中，lj为所述标识向量L的第j个元素，j＝1,2,…,N-1，为所述延迟响应向量Sf中所有元素的平均值，为所述上升响应向量Sb中所有元素的平均值；分别计算所述延迟响应向量Sf中各元素与平均值的差值绝对值之和以及所述上升响应向量Sb中各元素与平均值的差值绝对值之和df(n)=1nΣlj∈Sf|lj-cf(n)|,]]>db(n)=1N-n-1Σlj∈Sb|lj-cb(n)|;]]>计算和的和D(n)：D(n)=df(n)+db(n);]]>将D(n)保存在特征集合D中；S3.3检测n是否等于N-1，若n≠N-1，进入步骤S3.4，若n＝N-1，进入步骤S3.5；S3.4n增加1，重复执行步骤S3.2和S3.3；S3.5获得特征集合D＝[D(n)]1×(N-1)，其中，n＝1,2,…,N-1，提取所述特征集合D中所有元素的最小值当n＝N1时，为所述特征集合D中所有元素的最小值；S3.6获得所述延迟响应向量Sf和所述上升响应向量Sb，所述延迟响应向量Sf包含所述标识向量L的前N1个元素，所述上升响应向量Sb包含所述标识向量L的后N-N1-1个元素。在上述技术方案的基础上，步骤S4具体包括：所述延迟时间为τ＝N1×Ts。在上述技术方案的基础上，所述测试方法还包括：根据所述上升响应向量确定所述离散动态系统的时间常数。在上述技术方案的基础上，所述离散动态系统的总延时为所述延迟时间与所述时间常数之和。与现有技术相比，本发明的优点如下：(1)本发明通过向离散动态系统输入阶跃信号，获得离散动态系统的阶跃响应输出值，并根据作为阶跃响应输出值的阶跃响应采样时间序列，通过对采样时间序列进行奇异值分解构造标识向量，以及依据给出的计算方法将标识向量划分为延迟响应向量和上升响应向量，延迟响应向量包含标识向量中的前N1个元素，上升响应向量包含标识向量中的后N-N1-1个元素，根据延迟响应向量计算延迟时间。本发明能够克服测量噪声的干扰，准确确定延迟时间，计算结果重复性好。(2)本发明还可以根据上升响应向量准确确定离散动态系统的时间常数，并准确确定离散动态系统的总延时为延迟时间与时间常数之和。附图说明图1为离散动态系统阶跃输入的响应序列；图2为本发明实施例中一种离散动态系统时延特性的测试方法的流程图；图3为图2中S3的具体流程图。具体实施方式下面结合附图及具体实施例对本发明作进一步的详细描述。参见图2所示，本发明实施例提供一种离散动态系统时延特性的测定方法，包括以下步骤：S1.向离散动态系统输入阶跃信号，获得离散动态系统的阶跃响应输出值，阶跃响应输出值为采样时间序列yi，i＝1,2,…,N，其中，i为采样点的序号，yi为第i个采样点的值，N为采样点总数，且N为正整数，T为总采样时间，TS为采样周期。S2.根据阶跃响应采样时间序列yi，构造标识向量。其中，步骤S2具体包括：S2.1根据阶跃响应采样时间序列yi，构造数据矩阵Z：Z=y1y2...yN-1y2y3...yN2×(N-1),]]>其中，数据矩阵Z的下标2×(N-1)表示该矩阵为2行N-1列的矩阵。数据矩阵Z的构造方法为:将离散动态系统的阶跃响应采样时间序列yi中前N-1个采样点的值作为数据矩阵Z的第一行，采样时间序列yi中后N-1个采样点的值作为数据矩阵Z的第二行。对数据矩阵Z进行奇异值分解：Z＝Q2×2G2×2V2×(N-1)，其中，Q为正交矩阵，G为对角矩阵，V为行正交矩阵。S2.2根据矩阵V，构造关系矩阵M：H=V(N-1)×2T×V2×(N-1),]]>其中，M为N-1行N-1列的矩阵，矩阵VT为矩阵V的转置矩阵。对关系矩阵M进行奇异值分解：M=W(N-1)×2Σ2×2W2×(N-1)T,]]>其中，Σ为对角矩阵，WT为W的转置矩阵，W为列正交矩阵，W=w11w12w21w22......w(N-1)1w(N-1)2(N-1)×2.]]>S2.3截取W矩阵的后K行构造子矩阵X：X=w(N-K+1)1w(N-K+1)2w(N-K+2)1w(N-K+2)2......w(N-1)1w(N-1)2K×2,]]>其中，2≤K≤N-1。计算加权向量δ：δ=(X2×KTXK×2)-1X2×KT1K×1,]]>其中，XT为X的转置矩阵，XTX为两个矩阵XT和X相乘得到的矩阵，(XTX)-1为两个矩阵XT和X相乘得到的矩阵XTX的逆矩阵，1K×1为列向量，1K×1中的元素个数为K，并且所有元素的值均为1，δ为2行1列矩阵，即列向量。其中，为确保加权向量δ解的唯一性，要求K取值大于等于δ的维数，即2≤K≤N-1，。此外，K取值越大，则计算加权向量δ的抗噪声能力越强，K取值受限于上升响应向量的维数，即N-N1-1。S2.4计算标识向量L：L＝W(N-1)×2×δ2×1，其中，标识向量L为N-1行1列矩阵，即元素个数为N-1的列向量。标识向量L的物理本质在于指示离散动态系统的延迟时间τ对应的延迟响应和其后的非延迟响应。其中，标识向量L中元素的值越接近0，则表示该元素对应的响应输出值越有可能是延迟响应，标识向量L的元素的值越接近1，则表示该元素对应的响应输出值越有可能是非延迟响应。S3.将标识向量依据给出的计算方法划分为延迟响应向量和上升响应向量，延迟响应向量包含标识向量中的前N1个元素，上升响应向量包含标识向量中的后N-N1-1个元素，其中，1≤N1≤N-1。步骤S3基于标识向量L的物理本质，将标识向量L中的元素分为延迟响应向量和上升响应向量，其中延迟响应向量对应离散动态系统的延迟时间τ对应的延迟响应。延迟响应向量和上升响应向量的划分是基于各向量中的各元素的值与该向量的平均值的差值的绝对值之和最小。参见图3所示，步骤S3具体包括：S3.1将标识向量L依据给出的计算方法划分为延迟响应向量和上升响应向量，其中，先将延迟响应向量Sf的元素个数n设为1，其中，n＝1,2,…,N-1，则上升响应向量Sb的元素个数为N-n-1＝N-2。延迟响应向量Sf包含标识向量L的前n个元素lj，lj为标识向量L的第j个元素，j＝1,2,…,N-1，上升响应向量Sb包含标识向量L的后N-n-1个元素lj。S3.2分别计算从S3.1中获得的延迟响应向量Sf和上升响应向量Sb中所有元素的平均值：cf(n)=1nΣlj∈Sflj,]]>cb(n)=1N-n-1Σlj∈Sblj,]]>其中，lj为标识向量L的第j个元素，j＝1,2,…,N-1，为延迟响应向量Sf中所有元素的平均值，为上升响应向量Sb中所有元素的平均值。分别计算延迟响应向量Sf中各元素与平均值的差值绝对值之和以及上升响应向量Sb中各元素与平均值的差值绝对值之和df(n)=1nΣlj∈Sf|lj-cf(n)|,]]>db(n)=1N-n-1Σlj∈Sb|lj-cb(n)|;]]>计算和的和D(n)：D(n)=df(n)+db(n).]]>将D(n)保存在特征集合D中。S3.3检测n是否等于N-1，若n≠N-1，进入步骤S3.4，若n＝N-1，进入步骤S3.5。S3.4n增加1，重复执行步骤S3.2和S3.3。S3.5获得特征集合D＝[D(n)]1×(N-1)，其中，n＝1,2,…,N-1，提取特征集合D中所有元素的最小值当n＝N1时，为特征集合D中所有元素的最小值。当n依次为1,2,…,N-1时，步骤3.2分别计算出D(n)的值，并依次保存在特征集合D中，最终获得特征集合D＝[D(n)]1×(N-1)。S3.6获得延迟响应向量Sf和上升响应向量Sb，延迟响应向量Sf包含标识向量L的前N1个元素，上升响应向量Sb包含标识向量L的后N-N1-1个元素。S4.根据延迟响应向量Sf计算延迟时间τ。步骤S4具体包括：延迟时间为τ＝N1×Ts。本测定方法还可以根据上升响应向量Sb确定离散动态系统的时间常数。离散动态系统的总延时为延迟时间τ与时间常数t之和。本发明通过向离散动态系统输入阶跃信号，获得离散动态系统的阶跃响应输出值，并根据作为阶跃响应输出值的阶跃响应采样时间序列，通过对采样时间序列进行奇异值分解构造标识向量，以及依据统计方法将标识向量划分为延迟响应向量和上升响应向量，延迟响应向量包含标识向量中的前N1个元素，上升响应向量包含标识向量中的后N-N1-1个元素，根据延迟响应向量计算延迟时间。本发明能够克服测量噪声的干扰，准确确定延迟时间，测量结果重复性好。本发明还可以根据上升响应向量准确确定离散动态系统的时间常数，并准确确定离散动态系统的总延时为延迟时间与时间常数之和。本发明的一种实施例如下：该实施例中，采样周期为Ts＝1秒，采样点总数N＝12。S1.向离散动态系统输入阶跃信号，获得离散动态系统的阶跃响应输出值，阶跃响应输出值为采样时间序列yi如表1所示。表1：本实施例中阶跃响应输出值采样时间序列yi序列123456789101112数值0.29980.34860.50390.50971.4982.17362.83333.4493.94254.554.85765.0202S2.根据阶跃响应采样时间序列yi，构造标识向量。其中，步骤S2具体包括：S2.1根据阶跃响应采样时间序列yi，构造数据矩阵Z，如表2所示：表2：本实施例中得到的构造数据矩阵Z0.29980.34860.50390.50971.49802.17362.83333.44903.94254.55004.85760.34860.50390.50971.49802.17362.83333.44903.94254.55004.85765.0202对数据矩阵Z进行奇异值分解得到行正交矩阵V，如表3所示：表3：本实施例中得到的行正交矩阵V-0.0326-0.0431-0.0507-0.1035-0.1857-0.2524-0.3160-0.3710-0.4264-0.4712-0.49430.00640.0849-0.04910.72250.37150.28700.18200.02040.0575-0.2430-0.3898S2.2根据矩阵V，构造关系矩阵M，如表4所示：表4：本实施例中得到的关系矩阵M-0.03260.0064-0.0551-0.0353-0.1501-0.2245-0.2977-0.3677-0.4194-0.4922-0.5289-0.04310.08490.0441-0.7287-0.3873-0.3096-0.2112-0.0556-0.09770.19700.3408-0.0507-0.04910.99520.02900.00830.0010-0.0071-0.0174-0.0184-0.0348-0.0429-0.10350.72250.02790.5115-0.2634-0.2135-0.1498-0.0477-0.07740.11770.2128-0.18570.37150.0076-0.26090.8426-0.1407-0.1166-0.0719-0.0941-0.00100.0443-0.25240.28700.0004-0.2096-0.13970.8659-0.1226-0.0945-0.1173-0.0513-0.0193-0.31600.1820-0.0077-0.1444-0.1144-0.12150.8757-0.1157-0.1383-0.1049-0.0889-0.37100.0204-0.0179-0.0410-0.0685-0.0920-0.11420.8670-0.1531-0.1675-0.1750-0.42640.0575-0.0190-0.0697-0.0903-0.1146-0.1368-0.15340.8224-0.1847-0.1887-0.4712-0.2430-0.03510.12700.0046-0.0463-0.1008-0.1650-0.18140.7256-0.3204-0.4943-0.3898-0.04300.22300.0508-0.0132-0.0835-0.1710-0.1837-0.31880.6147并对关系矩阵M进行奇异值分解，得到列正交矩阵W，如表5所示。表5：本实施例中得到的列正交矩阵W0.0099-0.03170.0891-0.0338-0.0434-0.05560.7295-0.02580.3892-0.14500.3123-0.22030.2147-0.29470.0599-0.36670.1026-0.4179-0.1914-0.4944-0.3348-0.5330S2.3截取W矩阵的后K行构造子矩阵X，例如，设K＝3，如表6所示。表:6：本实施例中得到的子矩阵X0.1026-0.4179-0.1914-0.4944-0.3348-0.5330计算加权向量δ：δ=0.5911-2.2489]]>S2.4计算标识向量L，如表7所示。表7：本实施例中得到的标识向量L。0.09740.20420.09351.00000.88480.98851.06331.05841.24991.07981.0000S3.将标识向量L依据设定的统计方法划分为延迟响应向量Sf和上升响应向量Sb，计算获得其特征集合D，如表8所示。提取特征集合D中所有元素的最小值当n＝N1时，为特征集合D中所有元素的最小值，N1＝3，即延迟响应向量Sf包含标识向量L中的前N1＝3个元素。表8：本实施例中得到的特征集合D0.35700.32290.24040.51280.60230.67060.75820.89411.23652.4640S4.根据延迟响应向量Sf计算延迟时间τ，延迟时间τ为：τ＝N1×Ts＝3秒。本发明不局限于上述实施方式，对于本
技术领域：
的普通技术人员来说，在不脱离本发明原理的前提下，还可以做出若干改进和润饰，这些改进和润饰也视为本发明的保护范围之内。本说明书中未作详细描述的内容属于本领域专业技术人员公知的现有技术。当前第1页1 2 3