一种MIMOOTA信道建模方法及装置与流程

本发明涉及无线通信技术领域，特别涉及一种MIMO OTA信道建模方法及装置。

背景技术：

多输入多输出(Multiple Input Multiple Output，MIMO)技术由于可以极大的改善通信系统的性能，满足人们对于通信质量与速度等方面的需求，已经大量的应用到目前的终端设备制造中。广大设备生产厂商以及网络运营商正在大力推进对于MIMO设备进行性能检测方法的研究。其中，多输入多输出空中特性(Over The Air，OTA)测试技术能模拟真实的信道环境，从而成为了对MIMO设备性能进行测试的可靠方法，已经受到了学术界和工业界的广泛关注。3GPP、CTIA等组织已经启动了对于MIMO OTA测试技术的标准化研究工作，目前公认的可靠方法之一是基于吸波暗室的多探针法。

基于吸波暗室的多探针法首先在吸波暗室中配置若干探针，信道仿真器产生所需的信道模型，通过探针传输到吸波暗室中，产生的信号在测试区域进行组合，从而再现多径信号真实的传播过程。

在基于吸波暗室的多探针法中，按照仿真原理的区别，分为预衰落合成(Pre-Faded Signal Sythesis，PFS)技术和平面波合成(Plane Wave Synthesis，PWS)技术。PFS技术根据目标场景的功率谱密度分布及目标信道的空间相关性，为每个探针分配不同的权重，从而实现信号的空间域与时间域的实际场景再现。它模拟了多径信号在不存在视距传输情况下，到达待测设备的场景。

在使用PFS技术的过程中，如何计算分配给各个探针的权重是一个随机寻优问题，现有技术中使用凸优化算法(Convex Algorithm，CA)进行求解，但是使用凸优化算法进行求解时，由于目标函数和约束条件可能是非线性的以及目标函数和约束条件不总是凸的，导致在求解过程中目标函数和约束条件难以转化为标准凸优化形式，存在无法求出解的情况，进而存在无法计算出分配给各个探针的权重的问题，最终导致测试所需的信道模型不精确。

技术实现要素：

本发明实施例公开了一种MIMO OTA信道建模方法及装置，用于计算出分配给每个探针的权重，进而根据计算出的每个探针对应的权重形成所需要的信道模型。

为达到上述目的，本发明实施例公开了一种MIMO OTA信道建模方法，包括：

构建与测试场景所对应的初始信道模型，其中，所述初始信道模型为基于吸波暗室的MIMO OTA测试模型，且所述初始信道模型中包括M个探针；

利用模拟退火算法，计算所述初始信道模型中各个探针所对应的权重值；

为所述初始信道模型中各个探针设置所计算出的相应权重值，形成所述测试场景所对应的目标信道模型；

其中，所述模拟退火算法，计算多个探针所对应的权重值，包括：

S1，设置初始温度T、温度递减系数α、温度终止界限T-end、迭代次数L，以及各个探针所对应的第一类随机权重值W1为预设值，其中，所述第一类随机权重值W1的数量与探针的数量相同；

S2，为各个探针构建第二类随机权重值W2，其中，所述第二类随机权重值W2的数量与探针的数量相同；

S3，利用所述第一类随机权重值W1和第二类随机权重值W2，确定第一评价函数C1和第二评价函数C2；

S4，根据第二评价函数C2与第一评价函数C1的差值△t，确定各个探针所对应的备用权重值，并将所述确定的备用权重值更新为新的第一类随机权重值W1，其中，△t＝C2-C1；

S5，判断是否执行了迭代次数L次，如果是，则令T’＝α×T，并执行S6，如果否，返回到S2；

S6，判断是否满足T’<T-end，如果满足，将各个探针所对应的备用权重值分别作为所述初始信道模型中相应探针所对应的权重值，若不满足，将T更新为T’，返回到S2。

较佳地，所述根据第二评价函数C2与第一评价函数C1的差值△t，确定各个探针所对应的备用权重值，包括：

判断第二评价函数C2与第一评价函数C1的差值△t是否满足△t>0；

若满足，产生一个在0-1之间的随机数K，判断随机数K是否小于概率exp(△t/T)，若小于，确定当前的第二类随机权重值W2作为各个探针所对应的备用权重值，若不小于，确定当前的第一类随机权重值W1作为各个探针所对应的备用权重值；

若不满足，确定当前的第二类随机权重值W2作为各个探针所对应的备用权重值；

将所述确定的备用权重值更新为新的第一类随机权重值W1。

较佳地，M个探针所对应的第一类随机权重值W1之和为1；

M个探针所对应的第二类随机权重值W2之和为1。

较佳地，所述利用所述第一类随机权重值W1和第二类随机权重值W2，确定第一评价函数C1和第二评价函数C2，包括：

确定理论空间相关系数ρ分布；

利用第一类随机权重值W1，确定第一仿真空间相关系数分布，利用第二类随机权重值W2，确定第二仿真空间相关系数分布；

利用理论空间相关系数ρ分布、第一类随机权重值W1以及第一仿真空间相关系数分布，确定第一评价函数C1，利用理论空间相关系数ρ分布、第二类随机权重值W2以及第二仿真空间相关系数分布，确定第二评价函数C2。

其中，确定第一评价函数C1和第二评价函数C2的过程的公式为：

$C1=\sqrt{\frac{1}{M}\underset{m=1}{\overset{M}{\&Sigma;}}|\mathrm{\&rho;}-\widehat{{\mathrm{\&rho;}}_1}{|}^2}$

$C2=\sqrt{\frac{1}{M}\underset{m=1}{\overset{M}{\&Sigma;}}|\mathrm{\&rho;}-\widehat{{\mathrm{\&rho;}}_2}{|}^2}$

其中，和分别是包含测试区域内取样点u和v位置信息的向量，是空间角度Ω的联合矩阵，k是波数，P(Ω)是到达功率谱密度函数，W1_m为第m个探针的第一类随机权重值，W2_m为第m个探针的第二类随机权重值，为第m个探针的位置向量。

为达到上述目的，本发明实施例公开了一种MIMO OTA信道建模装置，包括：

构建模块，用于构建与测试场景所对应的初始信道模型，其中，所述初始信道模型为基于吸波暗室的MIMO OTA测试模型，且所述初始信道模型中包括M个探针；

计算模块，用于利用模拟退火算法，计算所述初始信道模型中各个探针所对应的权重值；

设置模块，用于为所述初始信道模型中各个探针设置所计算出的相应权重值，形成所述测试场景所对应的目标信道模型；

其中，所述计算模块，包括：

设置子单元，用于设置初始温度T、温度递减系数α、温度终止界限T-end、迭代次数L，以及各个探针所对应的第一类随机权重值W1为预设值，其中，所述第一类随机权重值W1的数量与探针的数量相同；

构建子单元，用于为各个探针构建第二类随机权重值W2，其中，所述第二类随机权重值W2的数量与探针的数量相同；

第一确定子单元，用于利用所述第一类随机权重值W1和第二类随机权重值W2，确定第一评价函数C1和第二评价函数C2；

第二确定子单元，用于根据第二评价函数C2与第一评价函数C1的差值△t，确定各个探针所对应的备用权重值，并将所述确定的备用权重值更新为新的第一类随机权重值W1，其中，△t＝C2-C1；

第一判断子单元，用于判断是否执行了迭代次数L次，如果是，则令T’＝α×T，并触发第二判断子单元，如果否，触发构建子单元；

第二判断子单元，用于判断是否满足T’<T-end，如果满足，将各个探针所对应的备用权重值分别作为所述初始信道模型中相应探针所对应的权重值，若不满足，将T更新为T’，触发构建子单元。

较佳地，所述第二确定子单元，具体用于：

判断第二评价函数C2与第一评价函数C1的差值△t是否满足△t>0；

若满足，产生一个在0-1之间的随机数K，判断随机数K是否小于概率exp(△t/T)，若小于，确定当前的第二类随机权重值W2作为各个探针所对应的备用权重值，若不小于，确定当前的第一类随机权重值W1作为各个探针所对应的备用权重值；

若不满足，确定当前的第二类随机权重值W2作为各个探针所对应的备用权重值；

将所述确定的备用权重值更新为新的第一类随机权重值W1。

较佳地，M个探针所对应的第一类随机权重值W1之和为1；

M个探针所对应的第二类随机权重值W2之和为1。

较佳地，所述第一确定子单元，具体用于：

确定理论空间相关系数ρ分布；

利用第一类随机权重值W1，确定第一仿真空间相关系数分布，利用第二类随机权重值W2，确定第二仿真空间相关系数分布；

利用理论空间相关系数ρ分布、第一类随机权重值W1以及第一仿真空间相关系数分布，确定第一评价函数C1，利用理论空间相关系数ρ分布、第二类随机权重值W2以及第二仿真空间相关系数分布，确定第二评价函数C2。

其中，确定第一评价函数C1和第二评价函数C2的过程的公式为：

$C1=\sqrt{\frac{1}{M}\underset{m=1}{\overset{M}{\&Sigma;}}|\mathrm{\&rho;}-\widehat{{\mathrm{\&rho;}}_1}{|}^2}$

$C2=\sqrt{\frac{1}{M}\underset{m=1}{\overset{M}{\&Sigma;}}|\mathrm{\&rho;}-\widehat{{\mathrm{\&rho;}}_2}{|}^2}$

其中，和分别是包含测试区域内取样点u和v位置信息的向量，是空间角度Ω的联合矩阵，k是波数，P(Ω)是到达功率谱密度函数，W1_m为第m个探针的第一类随机权重值，W2_m为第m个探针的第二类随机权重值，为第m个探针的位置向量。

由上述技术方案可知，本发明实施例公开了一种MIMO OTA信道建模方法及装置，方法中包括构建与测试场景所对应的初始信道模型，其中，所述初始信道模型为基于吸波暗室的MIMO OTA测试模型，且所述初始信道模型中包括M个探针；利用模拟退火算法，计算所述初始信道模型中各个探针所对应的权重值；为所述初始信道模型中各个探针设置所计算出的相应权重值，形成所述测试场景所对应的目标信道模型。相比于现有技术，应用本发明实施例，无需考虑目标函数和约束条件的凹凸限制问题，可以计算出分配给每个探针的权重，进而可以根据计算出的每个探针对应的权重获得信道模型。

附图说明

为了更清楚地说明本发明实施例或现有技术中的技术方案，下面将对实施例或现有技术描述中所需要使用的附图作简单地介绍，显而易见地，下面描述中的附图仅仅是本发明的一些实施例，对于本领域普通技术人员来讲，在不付出创造性劳动的前提下，还可以根据这些附图获得其他的附图。

图1为本发明实施例所公开的一种MIMO OTA信道建模方法的流程示意图；

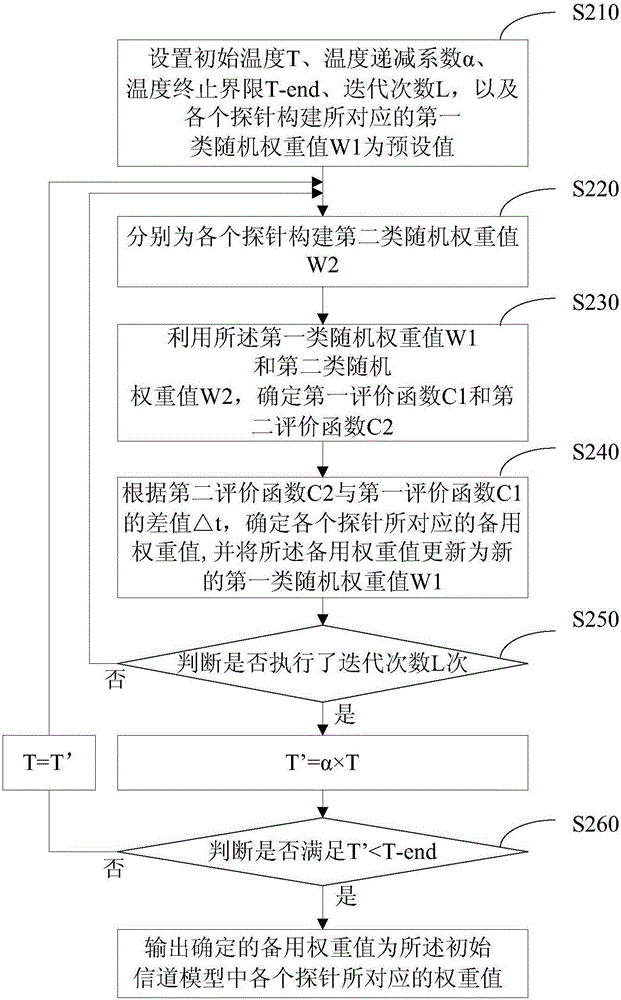
图2为本发明实施例所公开的一种MIMO OTA信道建模方法中的模拟退火 算法的流程示意图；

图3为本发明实施例所公开的一种MIMO OTA信道建模方法中的模拟退火算法中的步骤S240具体过程的流程示意图；

图4本发明实施例所公开的一种MIMO OTA信道建模装置的结构示意图。

具体实施方式

下面将结合本发明实施例中的附图，对本发明实施例中的技术方案进行清楚、完整地描述，显然，所描述的实施例仅仅是本发明一部分实施例，而不是全部的实施例。基于本发明中的实施例，本领域普通技术人员在没有付出创造性劳动前提下所获得的所有其他实施例，都属于本发明保护的范围。

本发明实施例公开了一种MIMO OTA信道建模方法及装置，以下进行详细说明。

本发明实施例公开了一种MIMO OTA信道建模方法，如图1所示，包括以下步骤：

步骤S110，构建与测试场景所对应的初始信道模型；

其中，所述初始信道模型为基于吸波暗室的MIMO OTA测试模型，且所述初始信道模型中包括M个探针。

测试的场景可以是二维的，也可以是三维的，相应的，构建的与测试场景所对应的初始信道模型可以是二维模型，也可以是三维模型。

具体的，测试场景为真实情况下测试对象可能处在的区域，比如建筑物密集的城区、建筑物稀少的郊区等。其中，该测试对象为含有MIMO天线的设备，如手机终端、电脑或PAD等。

需要说明的是，可以通过现有技术中任一种信道仿真过程中构建模型的方法构建与测试场景所对应的初始信道模型。

步骤S120，利用模拟退火算法，计算所述初始信道模型中各个探针所对应的权重值；

模拟退火(Simulated Annealing，SA)算法是基于蒙特卡洛迭代求解策略的一种随机寻优算法，其出发点是基于物理退火过程与组合优化之间的相似性。 本实施例利用随机取优的原理，通过在SA算法计算过程加入限制条件，对目标函数和约束条件进行求解，无需考虑目标函数和约束条件的凹凸性。

为了方案布局清晰，后续对利用模拟退火算法，计算所述初始信道模型中各个探针所对应的权重值的过程进行详细介绍。

步骤S130，为所述初始信道模型中各个探针设置所计算出的相应权重值，形成所述测试场景所对应的目标信道模型；

具体地，计算出各个探针设置所计算出的相应权重值后，为所述初始信道模型中每一各探针设置所计算出的相应的权重值，从而形成所述测试场景所对应的目标信道模型，具体可以参考现有技术中根据各个探针的权重值形成信道模型的方法形成目标信道模型，本实施例不再赘述。

应用本发明实施例，无需考虑目标函数和约束条件的凹凸限制问题，利用随机取优的原理，采用模拟退火算法对目标函数和约束条件进行求解，计算出了分配给各个探针的权重，进而根据计算出的各个探针对应的权重获得信道模型。

下面介绍利用模拟退火算法，计算所述初始信道模型中各个探针所对应的权重值的过程，如图2所示，具体过程包括：

步骤S210，设置初始温度T、温度递减系数α、温度终止界限T-end、迭代次数L，以及各个探针所对应的第一类随机权重值W1为预设值，其中，所述第一类随机权重值W1的数量与探针的数量相同；

模拟退火算法的原理是由某一较高初温开始，利用具有概率突跳特性的抽样策略在解空间中进行随机搜索，伴随温度的不断下降重复抽样过程，最终得到问题的全局最优解，因此需要预先为参数初始温度T、温度递减系数α、温度终止界限T-end以及迭代次数L设置预设值。

具体地，可以根据经验设置初始温度T、温度递减系数α、温度终止界限T-end的预设值，根据计算速率以及精确度设置迭代次数L的预设值。

为初始信道模型中包括的每一个探针所对应的第一类随机权重值W1设置预设值，其中，第一类随机权重值W1的数量与探针的数量相同。

需要说明的是，M个第一类随机权重值W1是随机产生的一组随机数，且第 一类随机权重值W1是为各个探针的假设的权重值，M个第一类随机权重值W1之和为1。

因此，在SA算法计算各个探针权重的过程中，要加入M个探针所对应的第一类随机权重值W1之和为1的限制条件。

步骤S220，为各个探针构建第二类随机权重值W2；

具体地，为初始信道模型中包括的每一个探针构建第二类随机权重值W2，其中，第二类随机权重值W2的数量与探针的数量相同。

需要说明的是，M个第二类随机权重值W2是随机产生的一组随机数，且第二类随机权重值W2是为各个探针的假设的权重值，M个第二类随机权重值W2之和为1。

因此，在SA算法计算各个探针权重的过程中，要加入M个探针所对应的第二类随机权重值W2之和为1的限制条件。

可以理解的是，上述步骤中“第一类随机权重值W1”中的“第一”和“第二类随机权重值W2”中的“第二”，仅仅用于从命名上区分两类随机权重值，并不具有任何限定意义。

步骤S230，利用所述第一类随机权重值W1和第二类随机权重值W2，确定第一评价函数C1和第二评价函数C2；

具体地，利用初始信道模型中包括的每一个探针的第一类随机权重值W1和第二类随机权重值W2，确定第一评价函数C1和第二评价函数C2。

作为本实施例的一种优选方案，利用第一类随机权重值W1和第二类随机权重值W2，确定第一评价函数C1和第二评价函数C2的过程，可以包括以下过程：

首先，确定理论空间相关系数ρ分布；

具体的：对于所要仿真的信道环境，确定信号的到达功率角度谱，选择信道模型，得到相应的到达功率谱密度，利用公式：确定理论空间相关系数ρ分布，其中，和分别是包含测试区域内取样点u和v位置信息的向量，所述取样点的位置为实际测量时假设天线放置的位置，是空间角度Ω的联合矩阵，k是波数，P(Ω)是到达功率谱密度函数。

然后，利用第一类随机权重值W1，确定第一仿真空间相关系数分布，利用第二类随机权重值W2，确定第二仿真空间相关系数分布；

具体地，探针发送信号时，每个探针发送的信号有着不同的幅度和分布，这就要求不同位置的探针具备不同的权重，利用第一类随机权重值W1以及公式：确定第一仿真空间相关系数分布的表达式；利用第二类随机权重值W2以及公式：确定第二仿真空间相关系数分布的表达式；其中，W1_m为第m个探针的第一类随机权重值，W2_m为第m个探针的第二类随机权重值，为第m个探针的位置向量。

最后，利用理论空间相关系数ρ分布、第一类随机权重值W1以及第一仿真空间相关系数分布，确定第一评价函数C1，利用理论空间相关系数ρ分布、第二类随机权重值W2以及第二仿真空间相关系数分布，确定第二评价函数C2；

具体地，评价函数为理论空间相关系数和仿真空间相关系数的均方误差，利用公式：确定第一评价函数C1；利用公式： 确定第二评价函数C2。

可以理解的是，“第一仿真空间相关系数”中的“第一”和“第二仿真空间相关系数”中的“第二”，以及“第一评价函数”中的“第一”和“第二评价函数”中的“第二”，仅仅用于从命名上区分两个相关系数以及评价函数，并不具有任何限定意义。

步骤S240，根据第二评价函数C2与第一评价函数C1的差值△t，确定各个探针所对应的备用权重值，并将所述确定的备用权重值更新为新的第一类随机权重值W1；

其中，第二评价函数C2与第一评价函数C1的差值△t为△t＝C2-C1。

作为本实施例的另一种优选方案，为了能够概率性的获得全局最优解，根据第二评价函数C2与第一评价函数C1的差值△t，确定各个探针所对应的备用权重值的过程，可以如图3所示，包括：

步骤S241，计算第二评价函数C2与第一评价函数C1的差值，△t＝C2-C1；

步骤S242，判断第二评价函数C2与第一评价函数C1的差值△t是否满足△t>0；若满足，产生一个在0-1之间的随机数K，并执行步骤S243，若不满足，确定当前的第二类随机权重值W2作为各个探针所对应的备用权重值；

步骤S243，判断随机数K是否小于概率exp(△t/T)，若小于，确定当前的第二类随机权重值W2作为各个探针所对应的备用权重值，若不小于，确定当前的第一类随机权重值W1作为各个探针所对应的备用权重值。

步骤S244，将所述确定的备用权重值更新为新的第一类随机权重值W1；

确定出各个探针所对应的备用权重值后，将各个探针所对应的备用权重值作为新的各个探针所对应的第一类随机权重值W1。

步骤S250，判断是否执行了迭代次数L次，如果是，则令T’＝α×T，并执行步骤S260，如果否，返回到步骤S220；

具体地，如果循环执行了迭代次数L次，表明在解空间内完成了所有搜索，即在随机权重值空间内完成了所有搜索，则进行降温步骤，即令T’＝α×T，如果循环没有执行迭代次数L次，表明在在解空间内没有完成所有搜索，即在随机权重值空间内没有完成所有搜索，则执行步骤S220，即重复分别为各个探针构建第一类随机权重值W1和第二类随机权重值W2的步骤。

步骤S260，判断是否满足T’<T-end，如果满足，将各个探针所对应的备用权重值分别作为所述初始信道模型中相应探针所对应的权重值，若不满足，将T更新为T’，返回到步骤S220；

具体地，如果满足T’<T-end，表明温度已降到预设条件以内，即已得到全局最优解，则将各个探针所对应的备用权重值分别作为所述初始信道模型中相应探针所对应的权重值，如果不满足T’<T-end，表明温度还没有降到预设条件以内，还不是全局最优解，则执行步骤S220，即重复分别为各个探针构建第一类随机权重值W1和第二类随机权重值W2的步骤。

本发明实施例还公开了一种MIMO OTA信道建模装置，如图4所示，包括：构建模块410，计算模块420，设置模块430，其中：

构建模块410，用于构建与测试场景所对应的初始信道模型，其中，所述初始信道模型为基于吸波暗室的MIMO OTA测试模型，且所述初始信道模型中包括M个探针；

计算模块420，用于利用模拟退火算法，计算所述初始信道模型中各个探针所对应的权重值；

设置模块430，用于为所述初始信道模型中各个探针设置所计算出的相应权重值，形成所述测试场景所对应的目标信道模型；

其中，所述计算模块420，包括：

设置子单元421，用于设置初始温度T、温度递减系数α、温度终止界限T-end、迭代次数L，以及各个探针所对应的第一类随机权重值W1为预设值，其中，所述第一类随机权重值W1的数量与探针的数量相同；

构建子单元422，用于为各个探针构建第二类随机权重值W2，其中，所述第二类随机权重值W2的数量与探针的数量相同；

第一确定子单元423，用于利用所述第一类随机权重值W1和第二类随机权重值W2，确定第一评价函数C1和第二评价函数C2；

第二确定子单元424，用于根据第二评价函数C2与第一评价函数C1的差值△t，确定各个探针所对应的备用权重值，并将所述确定的备用权重值更新为新的第一类随机权重值W1，其中，△t＝C2-C1；

第一判断子单元425，用于判断是否执行了迭代次数L次，如果是，则令T’＝α×T，并触发第二判断子单元，如果否，触发构建子单元；

第二判断子单元426，用于判断是否满足T’<T-end，如果满足，将各个探针所对应的备用权重值分别作为所述初始信道模型中相应探针所对应的权重值，若不满足，将T更新为T’，触发构建子单元421。

应用本实施例，无需考虑目标函数和约束条件的凹凸限制问题，利用随机取优的原理，采用模拟退火算法对目标函数和约束条件进行求解，计算出了分 配给各个探针的权重，进而根据计算出的各个探针对应的权重获得信道模型。

可选的，在一种具体实现方式中，所述第二确定子单元424，具体用于：

判断第二评价函数C2与第一评价函数C1的差值△t是否满足△t>0；

若满足，产生一个在0-1之间的随机数K，判断随机数K是否小于概率exp(△t/T)，若小于，确定当前的第二类随机权重值W2作为各个探针所对应的备用权重值，若不小于，确定当前的第一类随机权重值W1作为各个探针所对应的备用权重值；

若不满足，确定当前的第二类随机权重值W2作为各个探针所对应的备用权重值

将所述确定的备用权重值更新为新的第一类随机权重值W1。

可选的，在一种具体实现方式中，M个探针所对应的第一类随机权重值W1之和为1；

M个探针所对应的第二类随机权重值W2之和为1。

可选的，在一种具体实现方式中，所述第一确定子单元423，具体用于：

确定理论空间相关系数ρ分布；

利用第一类随机权重值W1，确定第一仿真空间相关系数分布，利用第二类随机权重值W2，确定第二仿真空间相关系数分布；

利用理论空间相关系数ρ分布、第一类随机权重值W1以及第一仿真空间相关系数分布，确定第一评价函数C1，利用理论空间相关系数ρ分布、第二类随机权重值W2以及第二仿真空间相关系数分布，确定第二评价函数C2。

可选的，在一种具体实现方式中，确定第一评价函数C1和第二评价函数C2的过程的公式为：

$C1=\sqrt{\frac{1}{M}\underset{m=1}{\overset{M}{\&Sigma;}}|\mathrm{\&rho;}-\widehat{{\mathrm{\&rho;}}_1}{|}^2}$

$C2=\sqrt{\frac{1}{M}\underset{m=1}{\overset{M}{\&Sigma;}}|\mathrm{\&rho;}-\widehat{{\mathrm{\&rho;}}_2}{|}^2}$

其中，和分别是包含测试区域内取样点u和v位置信息的向量，是空间角度Ω的联合矩阵，k是波数，P(Ω)是到达功率谱密度函数，W1_m为第m个探针的第一类随机权重值，W2_m为第m个探针的第二类随机权重值，为第m个探针的位置向量。

对于装置实施例而言，由于其基本相似于方法实施例，所以描述的比较简单，相关之处参见方法实施例的部分说明即可。

需要说明的是，在本文中，诸如第一和第二等之类的关系术语仅仅用来将一个实体或者操作与另一个实体或操作区分开来，而不一定要求或者暗示这些实体或操作之间存在任何这种实际的关系或者顺序。而且，术语“包括”、“包含”或者其任何其他变体意在涵盖非排他性的包含，从而使得包括一系列要素的过程、方法、物品或者设备不仅包括那些要素，而且还包括没有明确列出的其他要素，或者是还包括为这种过程、方法、物品或者设备所固有的要素。在没有更多限制的情况下，由语句“包括一个……”限定的要素，并不排除在包括所述要素的过程、方法、物品或者设备中还存在另外的相同要素。

本领域普通技术人员可以理解实现上述方法实施方式中的全部或部分步骤是可以通过程序来指令相关的硬件来完成，所述的程序可以存储于计算机可读取存储介质中，这里所称得的存储介质，如：ROM/RAM、磁碟、光盘等。

以上所述仅为本发明的较佳实施例而已，并非用于限定本发明的保护范围。凡在本发明的精神和原则之内所作的任何修改、等同替换、改进等，均包含在本发明的保护范围内。