一种非重构框架下的信号估计方法与流程

本发明属于认知无线电参数识别和估计领域。

背景技术：

根据压缩感知理论，其主要研究内容包括对将信号进行稀疏分解和表示，设计合适的测量矩阵以及重构算法恢复信号内容。假设信号在某个变换域能够被稀疏表示，而且采样的测量矩阵和信号的稀疏矩阵不相关，因此能够从远远低于原始信号维度的少量非自适应的测量值以较高概率恢复出原始信号。在恢复信号内容时，重构算法占据着大量的计算资源。所以重构算法成为将压缩感知进行实际应用的瓶颈，成为亟待突破和解决的问题。

而信号的参数估计问题是推理问题，它不需要知道具体的信号形式和信号内容，因此在进行信号参数估计时可以完全省略信号的重构，直接利用压缩测量数据进行信号参数的识别，也就是所谓的非重构框架下的信号参数识别。

信号的循环谱能够区分数字调制信号在码速率、载波、调制方式上的不同，并且信号的循环谱具有特殊的稀疏性。按照所呈现出周期性统计特征划分，循环平稳信号可分为一阶(均值)、二阶(相关函数)和高阶(高阶累积量)循环平稳。数字调制信号的循环谱具有更高的稀疏性，利用循环谱高度的稀疏性可以减少参数估计算法运算量。

因此，亟需一种在无需对压缩信号进行重构，简化运算步骤，来获取信号参数的方法。

技术实现要素：

本发明是为了解决现有采用重构算法恢复信号时，存在重构速度慢，准确性差的问题，本发明提供了一种非重构框架下的信号估计方法。

一种非重构框架下的信号估计方法，该方法包括如下步骤：

步骤一：建立采样信号循环谱向量和采样信号循环自相关向量r_x的联系；

步骤二：建立采样信号压缩测量值自相关向量r_z和采样信号循环自相关向量r_x的联系；

步骤三：根据步骤一和步骤二获得的联系建立采样信号压缩测量值自相关向量r_z和采样信号循环谱向量的关系；

步骤四：删除采样信号循环谱向量中的冗余元素，获得简化后的采样信号循环谱向量

步骤五：利用采样信号压缩测量值自相关向量r_z和基于块稀疏的正交匹配追踪算法，对简化后的采样信号循环谱向量进行重构，获得原始信号循环谱；

步骤六：根据原始信号循环谱提取原始信号的参数信息，从而完成在非重构框架下的信号估计。

所述步骤一中建立采样信号循环谱向量和采样信号循环自相关向量r_x的联系的具体步骤为；

步骤一一：根据采样信号建立采样信号自相关矩阵R_x，其中，

采样信号自相关矩阵R_x满足n+v<N，因此，将采样信号自相关矩阵R_x去冗余后，转化为向量形式，获得采样信号循环自相关向量r_x，且

其中，表示对求均值，E{}表示求均值，x_t表示采样信号，表示采样信号的转置，r_x表示采样信号自相关向量，r_x(n,ν)表示索引为(n,ν)的自相关值，n表示时刻，ν表示延迟时间，x表示原始信号，x^*表示采样信号的共轭，T表示周期信号的周期，T_s表示采样周期，N表示总的采样点数；

步骤一二：由于采样信号自相关矩阵R_x沿对角对称，故，将采样信号自相关矩阵R_x中的重复元素置0，获得协方差辅助矩阵R，

步骤一三：定义协方差辅助矩阵R与采样信号循环自相关向量r_x之间的映射关系为，

vec{R}＝Br_x (公式四)，

其中，vec{·}表示矩阵向量化，B表示vec{R}与r_x的映射矩阵，

步骤一四：对协方差辅助矩阵R进行循环自相关操作，获得采样信号循环自相关矩阵其中

其中，G_v表示循环自相关操作矩阵，D_v表示选择矩阵；

步骤一五：对采样信号循环自相关矩阵作傅立叶变换，获得采样信号循环谱矩阵且

其中，F表示傅立叶变换矩阵，

步骤一六：对公式五中的采样信号循环自相关矩阵进行向量化操作，获得

其中，vec{}表示矩阵向量化，表示D_v的转置，表示直积，H表示采样信号循环自相关向量r_x与循环自相关向量之间的变换矩阵；

对公式六中的采样信号循环谱矩阵进行向量化操作，获得

其中，表示采样信号循环谱向量，F^-1表示傅立叶变换矩阵的逆，F^-T表示表示傅立叶变换矩阵的逆的转置，I_N表示N维的单位矩阵，W表示采样信号循环自相关向量与采样信号循环谱向量之间的变换矩阵，

步骤一七：根据公式七和公式八，建立采样信号循环谱向量和采样信号循环自相关向量r_x之间的变换关系，获得：

其中，表示矩阵H求伪逆。

所述的步骤二中建立采样信号压缩测量值自相关向量r_z和采样信号循环自相关向量r_x的联系的具体步骤为：

步骤二一：首先，对采样信号进行压缩，获得压缩测量值z_t，然后对原始信号x_t和压缩测量值z_t进行自相关操作，获得采样信号自相关矩阵R_x和采样信号压缩测量值自相关矩阵R_z，其中，z_t＝Ax_t，

定义采样信号自相关矩阵R_x与采样信号循环自相关向量r_x之间的映射关系为：

vec{R_x}＝P_Nr_x (公式十)，

定义采样信号压缩测量值自相关矩阵R_z与采样信号压缩测量值自相关向量r_z之间的映射关系为：

r_z＝Q_Mvec{R_z} (公式十一)，

其中，A表示测量矩阵，P_N表示采样信号自相关向量r_x与自相关矩阵向量vec{R_x}之间的映射矩阵，Q_M表示测量值自相关向量r_z与测量值自相关矩阵向量vec{R_z}的映射矩阵；

步骤二二：对等式z_t＝Ax_t两边同时进行自相关矩阵变换，获得R_z＝AR_xA^H，再

对等式R_z＝AR_xA^H两边同时向量化，获得

vec{R_z}＝vec{AR_xA^H} (公式十二)，

最后，将公式十和公式十一同时代入公式十二，获得采样信号压缩测量值自相关向量r_z和采样信号循环自相关向量r_x之间关系为：

其中，A^H表示测量矩阵A的转置，Φ表示压缩测量值自相关向量r_z与采样信号自相关向量r_x之间的变换矩阵。

所述的步骤三中，根据步骤一和步骤二建立采样信号压缩测量值自相关向量r_z和采样信号循环谱向量的关系的具体步骤为：

将公式九获得的采样信号循环自相关向量r_x代入到公式十三中，获得采样信号压缩测量值自相关向量r_z与采样信号循环谱向量的关系为：

其中，Ψ表示采样信号压缩测量值自相关向量r_z与采样信号循环谱向量之间的变换矩阵。

所述的vec{·}具有性质

其中，U、X和V均表示矩阵，V^T表示矩阵V的转置。

所述选择矩阵D_v，在位置(v,v)上，元素v＝1；其余位置上的元素均为0。

本发明设计思想：根据信号循环谱的定义，信号的频率由循环频率α划分为离散区域。信号的循环谱S(α,f)在|f|+|α|/2≤f_max区域内存在非零值，在双频率平面形成了菱形的支撑区，如图5中菱形支撑区所示，其数据处理点数为2f_max×4f_max。为了减少数据处理点数，可以将菱形区域进行平移如5中变换后支撑区所示，可以将数据处理点数降低为2f_max×2f_max。其中，α表示循环频率，f表示数字频率，f_max表示信号的最大频率。

BPSK信号循环谱如图6，信号循环谱为段稀疏，在循环双频率平面内只在少数区域呈现非零值，需要恢复出来的点数较少，因此可以利用其段稀疏的信息，减少恢复算法的运算复杂度。压缩感知的重构算法的目标向量必须满足稀疏性质，所以在不重构信号时域表达的前提下，只能根据信号的稀疏性来区分信号。调制信号的循环平稳特征完全满足这项要求，因为调制信号在双频率平面呈现出稀疏性，并且调制信号的高阶循环累积量仅在几个循环频率处为较大值，其余为零。

因此，利用压缩测量值直接估计出信号的二阶累积量，作为特征值提取各信号的循环频率。建立压采样信号压缩测量值自相关向量r_z与采样信号循环谱向量之间的关系。

本发明的基本思想是根据信号在信号二维频谱平面具有的高度稀疏和对称的特性，利用压缩感知获得少量测量点。传统的信号循环谱获得方式是根据测量值先恢复出原始的信号，再利用恢复出来的原始信号获取信号的二维循环谱。这样会大大增加系统的复杂度。

本发明是通过建立信号的测量值与二维循环谱之间的关系，根据循环谱的稀疏性利用基于块稀疏的正交匹配追踪算法得到信号的循环谱。该方法利用了所有信号映射的自相关函数的延时信息，信号的压缩率甚至可以延伸到非稀疏的段内信号当中。通过分析信号二阶循环统计特性的重要信息，为我们提供估计信号参数的一种新方式。

利用压缩感知测量值直接获得信号循环谱，根据数字调制信号在循环谱的稀疏性和其包含的丰富信息来进行信号参数估计任务。但是计算信号循环谱会带来极大的运算量，利用循环谱呈现的块稀疏性和对称性，本发明使用基于块恢复算法(BOMP)对信号的循环谱进行重构。与传统的正交匹配追踪算法(OMP)相比大大减少了运算时间。

本发明具体涉及在压缩采样下基于非重构的思想，利用通信调制信号的循环平稳特性对通信信号进行识别和检测的方法。

本发明带来的有益效果是，本发明具体是基于信号进行压缩感知后，获得的少量采样不经过对信号的重构，即：省略了对信号进行重构的过程，直接恢复出信号的循环谱，大大简化了运算的复杂度，运算速度提高了5％以上，提高了认知无线电系统在低信噪比环境下的检测能力。

附图说明

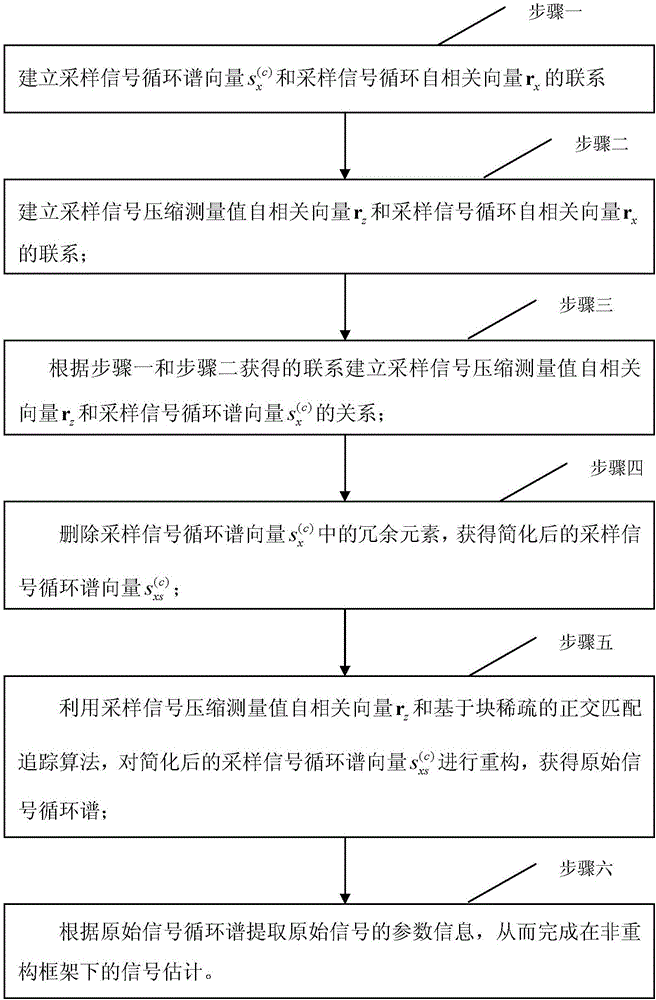
图1为本发明所述的一种非重构框架下的信号估计方法的流程图

图2为原始信号循环谱三维图。

图3为恢复出来的信号循环谱三维图。

图4为基于块稀疏的正交匹配追踪算法(BOMP)和传统的正交匹配追踪算法(OMP)的性能比较曲线；

图5为循环谱支撑区变换示意图。

图6为BPSK信号的循环谱三维图。

具体实施方式

具体实施方式一：参见图1说明本实施方式，本实施方式所述的一种非重构框架下的信号估计方法，该方法包括如下步骤：

步骤一：建立采样信号循环谱向量和采样信号循环自相关向量r_x的联系；

步骤二：建立采样信号压缩测量值自相关向量r_z和采样信号循环自相关向量r_x的联系；

步骤三：根据步骤一和步骤二获得的联系建立采样信号压缩测量值自相关向量r_z和采样信号循环谱向量的关系；

步骤四：删除采样信号循环谱向量中的冗余元素，获得简化后的采样信号循环谱向量

步骤五：利用采样信号压缩测量值自相关向量r_z和基于块稀疏的正交匹配追踪算法，对简化后的采样信号循环谱向量进行重构，获得原始信号循环谱；

步骤六：根据原始信号循环谱提取原始信号的参数信息，从而完成在非重构框架下的信号估计。

本实施方式，本发明，首先将信号经过测量矩阵获得欠奈奎斯特采样值，利用推导出来的测量值的相关值与信号的循环谱之间的联系，根据循环谱具有对称型和高度稀疏等特性简化构造信号循环谱的计算复杂度，利用基于块稀疏的正交匹配追踪算法获得信号的循环谱，进而提取出数字调制信号的参数，大大简化了运算的复杂度，提高了认知无线电系统在低信噪比环境下的检测能力。

基于块稀疏的正交匹配追踪算法是一种现有算法，该算法主要由三部分构成:相关测试、更新信号支撑块、更新残差。其中算法在每次相关测试时只找到信号支撑的一个块,对于块稀疏度为K的信号,至少要进行K次迭代才能恢复源信号,要求块稀疏度K已知且每次迭代找到信号支撑的一个块后,便不再改变。

在不压缩原始信号的情况下即压缩率M/N＝1时，获取的原始信号循环谱如图2所示。M表示测量值的长度，N表示采样信号的长度，利用压缩感知在压缩率M/N＝0.5时获取的恢复出来的信号循环谱如图3所示。基于块稀疏的正交匹配追踪算法(BOMP)与传统的正交匹配追踪算法(OMP)的性能对比，如图4所示，但是基于块的算法在运算时间上有较大的提升。表1为BOMP与OMP恢复算法运算时间对比,可知基于块的算法减少的运算点数，在不影响估计结果的情况下，大大节约了运算时间，参见表1。

表1算法运算时间对比

具体实施方式二：本实施方式与具体实施方式一所述的一种非重构框架下的信号估计方法的区别在于，所述步骤一中建立采样信号循环谱向量和采样信号循环自相关向量r_x的联系的具体步骤为；

步骤一一：根据采样信号建立采样信号自相关矩阵R_x，其中，

采样信号自相关矩阵R_x满足n+v<N，因此，将采样信号自相关矩阵R_x去冗余后，转化为向量形式，获得采样信号循环自相关向量r_x，且

其中，表示对求均值，E{}表示求均值，x_t表示采样信号，表示采样信号的转置，r_x表示采样信号自相关向量，r_x(n,ν)表示索引为(n,ν)的自相关值，n表示时刻，ν表示延迟时间，x表示原始信号，x*表示采样信号的共轭，T表示周期信号的周期，T_s表示采样周期，N表示总的采样点数；

步骤一二：由于采样信号自相关矩阵R_x沿对角对称，故，将采样信号自相关矩阵R_x中的重复元素置0，获得协方差辅助矩阵R，

步骤一三：定义协方差辅助矩阵R与采样信号循环自相关向量r_x之间的映射关系为，

vec{R}＝Br_x (公式四)，

其中，vec{·}表示矩阵向量化，B表示vec{R}与r_x的映射矩阵，

步骤一四：对协方差辅助矩阵R进行循环自相关操作，获得采样信号循环自相关矩阵其中

其中，G_v表示循环自相关操作矩阵，D_v表示选择矩阵；

步骤一五：对采样信号循环自相关矩阵作傅立叶变换，获得采样信号循环谱矩阵且

其中，F表示傅立叶变换矩阵，

步骤一六：对公式五中的采样信号循环自相关矩阵进行向量化操作，获得

其中，vec{}表示矩阵向量化，表示D_v的转置，表示直积，H表示采样信号循环自相关向量r_x与循环自相关向量之间的变换矩阵；

对公式六中的采样信号循环谱矩阵进行向量化操作，获得

其中，表示采样信号循环谱向量，F^-1表示傅立叶变换矩阵的逆，F^-T表示表示傅立叶变换矩阵的逆的转置，I_N表示N维的单位矩阵，W表示采样信号循环自相关向量与采样信号循环谱向量之间的变换矩阵，

步骤一七：根据公式七和公式八，建立采样信号循环谱向量和采样信号循环自相关向量r_x之间的变换关系，获得：

其中，表示矩阵H求伪逆。

具体实施方式三：本实施方式与具体实施方式二所述的一种非重构框架下的信号估计方法的区别在于，所述的步骤二中建立采样信号压缩测量值自相关向量r_z和采样信号循环自相关向量r_x的联系的具体步骤为：

步骤二一：首先，对采样信号进行压缩，获得压缩测量值z_t，然后对原始信号x_t和压缩测量值z_t进行自相关操作，获得采样信号自相关矩阵R_x和采样信号压缩测量值自相关矩阵R_z，其中，z_t＝Ax_t，

定义采样信号自相关矩阵R_x与采样信号循环自相关向量r_x之间的映射关系为：

vec{R_x}＝PNr_x (公式十)，

定义采样信号压缩测量值自相关矩阵R_z与采样信号压缩测量值自相关向量r_z之间的映射关系为：

r_z＝Q_Mvec{R_z} (公式十一)，

其中，A表示测量矩阵，P_N表示采样信号自相关向量r_x与自相关矩阵向量vec{R_x}之间的映射矩阵，Q_M表示测量值自相关向量r_z与测量值自相关矩阵向量vec{R_z}的映射矩阵；

步骤二二：对等式z_t＝Ax_t两边同时进行自相关矩阵变换，获得R_z＝AR_xA^H，再对等式R_z＝AR_xA^H两边同时向量化，获得

vec{R_z}＝vec{AR_xA^H} (公式十二)，

最后，将公式十和公式十一同时代入公式十二，获得采样信号压缩测量值自相关向量r_z和采样信号循环自相关向量r_x之间关系为：

其中，A^H表示测量矩阵A的转置，Φ表示压缩测量值自相关向量r_z与采样信号自相关向量r_x之间的变换矩阵。

具体实施方式四：本实施方式与具体实施方式三所述的一种非重构框架下的信号估计方法的区别在于，所述的步骤三中，根据步骤一和步骤二建立采样信号压缩测量值自相关向量r_z和采样信号循环谱向量的关系的具体步骤为：

将公式九获得的采样信号循环自相关向量r_x代入到公式十三中，获得采样信号压缩测量值自相关向量r_z与采样信号循环谱向量的关系为：

其中，Ψ表示采样信号压缩测量值自相关向量r_z与采样信号循环谱向量之间的变换矩阵。

具体实施方式五：本实施方式与具体实施方式二所述的一种非重构框架下的信号估计方法的区别在于，所述的vec{·}具有性质

其中，U、X和V均表示矩阵，V^T表示矩阵V的转置。

具体实施方式六：本实施方式与具体实施方式二所述的一种非重构框架下的信号估计方法的区别在于，所述选择矩阵D_v，在位置(v,v)上，元素v＝1；其余位置上的元素均为0。