基于事务和QoS的组合Web服务选择方法与流程
本发明涉及计算机网络技术领域,特别是基于事务和QoS的组合Web服务选择方法。
背景技术:
Web服务是一项业务之间自动交互的技术,企业能够发布它们的内部业务流程作为一个服务,然后在Web上提供它们的服务。随着应用的深入,业务流程可能包含一个或多个业务功能,由于这些业务可能调用来自不同组织的Web服务,所以需要按照一定方式组合来协同工作,并保证其运行的可靠性和结果的一致性。在复杂的网络环境中,由于面临以下问题,服务组合可能变得十分复杂:组件服务可能长时间运行,服务环境是松散匹配的和自身的异步性,由于机器失败导致的组合过程可能被取消,服务可能被移去或撤销,处理潜在的失败是必须的等等。因此,Web服务需要事务机制来保证输出的一致性及正确和可靠的执行。
在传统的组合服务选择方法分析中,研究者通常基于工作流的不同结构进行组合服务整合QoS(Quality of Service)分析,然后根据QoS进行组件的选择。但是,这些研究都没能考虑事务的要求。虽然事务的引入确保了组合服务的正确和可靠的执行,但它影响了组合服务的QoS属性。所以,需要提出一种方法来对基于事务和QoS的组合Web服务进行选择。
技术实现要素:
针对现有技术的问题,本发明提出了基于事务和QoS的组合Web服务选择方法。
基于事务和QoS的组合Web服务选择方法,该方法包括:
首先对Web服务赋予事务性,然后分析具有事务性要求服务的组合问题;
其次分析具有事务属性组合服务的性能问题;
最后,根据事务性组合服务的性能比较,提出基于事务和QoS的组合Web服务选择方法;该方法具体包括以下步骤:
第一步、在进行当前组件服务的选择时,根据前面已经选择合适组件服务的事务特点,并按照事务组合服务的规则要求,获得满足事务性要求的候选组件服务;
第二步、对每个候选组件服务进行性能评估,评估考虑Web服务的QoS和事务性要求;
第三步、重复以上过程,直到获得一个满足要求的组合服务。
所述第一步、第二步的具体内容如下:
在通常的服务选择方法,性能评估都是基于所有组件服务的QoS进行分析,本方法基于事务性和QoS,把两者相结合获取到基于事务的组合服务选择方法;
在基于事务的组合服务选择过程中,当一些功能性相似的候选组件服务可以被获得时,它们的非功能性要求QoS能够反映用户的需求,本方法提出Web服务ws下面三个QoS指标:
(1)执行价格(Execution price,EP):请求者调用服务ws所需要的花费,表示为qep(ws);
(2)执行时间(Execution time,ET):服务ws执行一次所需要的时间,表示为qet(ws);本方法认为服务执行一次的时间是相同的,并且在相同的时间内,服务执行一次可能失败,也可能成功完成;
(3)成功完成概率(Probability of Success,PS):服务ws成功完成用户请求的概率,表示为qps(ws);
其中,执行时间需要考虑组合服务的事务性带来的变化,分析过程如下:
(1)一个服务具有可补偿性,那么它能提供补偿策略来撤销该服务的影响,用符号“c”表示;
(2)一个服务具有可不断重试性,那么它能被重试,并且通过足够次数的重试达到最终成功,用符号“r”表示;
(3)一个服务具有中心点特性,那么它一旦执行成功,它的影响永远存在,而且不能被撤销,如果它执行失败,没有任何影响,用符号“p”表示;
由于网络环境的动态性、不确定性和开放性,来自不同组织的组件服务往往会调用失败,假设一个Web服务成功执行的概率为ps,服务执行一次的时间为t,那么在时间t内一个Web服务或者成功执行,或者执行失败,服务在前n-1次执行都失败,第n次执行成功的概率符合几何分布,概率函数为:
P(X=n)=(1-ps)n-1ps
X表示服务第几次执行,那么数学期望值为:
几何分布的数学期望反应的就是成功的平均执行次数,即成功执行的平均次数为1/ps,服务执行一次的时间为t,那么,成功执行的平均时间st为:
st=t/ps。
组合服务由基本组合模式构成,为分析事务组合服务的时间性能,现提出基本组合模式的时间性能分析方法;四种基本的组合模式分别是:序列模式、并行模式、选择模式和循环模式;并且服务组合由工作流模型来描述,TP表示事务性,TO表示一次执行时间,ST表示成功执行时间,PS表示成功执行概率;tp、to、st和ps表示组合服务相应概念的具体值;模式中每次只有一个组件服务执行失败。
(1)序列模式时间性能计算方法
序列模式用来定义组合服务由一系列按固定顺序执行的组件服务;在序列模式中,组件服务从左到右执行,当且仅当前面的组件服务成功执行完成后,后面的组件服务才能开始执行;如果有组件服务执行失败,将利用事务机制处理失败;前i个组件服务成功执行时间为sti,组件服务WSi执行一次的时间为ti,服务WSi成功执行的概率为psi;
首先考虑两个服务组成的组合序列模式,n个服务组成的组合模式可以看作前n-1服务的组合服务和第n个服务的组合;
在序列模式中,如果第一个服务WS1被赋予的事务特性为p或pr,WS1一旦成功完成,就不能被撤销,因此第二个服务WS2必须保证一定成功完成,即WS2必须包括r的事务性,所以WS2赋予事务性为pr或cr;{tp1,tp2}表示模式中从左到右或者从上到下的两个服务的事务性;
如果序列模式为{p,pr}或{p,cr},执行一次该模式,如果WS1执行失败,那么模式执行失败,时间为t1;如果WS1成功执行完成,由于WS2经过有限次数重试必定成功完成,所以模式成功执行完成,时间为t1+t2/ps2;那么在t1+t2/ps2时间内,判断该模式是否成功执行完成,故to=t1+t2/ps2;WS1成功执行完成概率为ps1,由于WS2经过有限次数重试必定成功完成,在模式执行过程中,事务性包含r的服务执行完成概率为1,即WS2成功执行完成概率为1;所以该组合服务的成功执行概率为ps=ps1,组合服务的事务性为p。
如果WS1执行失败,那么模式执行失败,为了分析该模式的成功完成时间,WS1将重复执行,直到WS1成功执行完成,那么模式成功完成;假设WS1的成功执行完成时间为st1,由于WS2经过有限次数重试必定成功完成,那么st=st1+t2/ps2;
如果序列模式为{pr,pr}或{pr,cr},执行一次模式,WS1和WS2都经过有限次数重试必定成功完成,那么to=t1/ps1+t2/ps2,执行一次时间也为成功执行完成时间,故st=st1+t2/ps。WS1和WS2成功执行完成概率都为1,那么模式成功执行的概率为ps=1,组合服务的事务性为pr;
在序列模式中,如果第一个服务WS1赋予的事务性是c或cr,那么如果第二个服务WS2执行失败,第一个服务执行可以被撤销,所以第二个服务WS2可以赋予任何事务性;
在序列模式中,如果模式为{p,pr}或{p,cr},那么,tp=p,to=t1+t2/ps2,st=st1+t2/ps2,ps=ps1;如果序列模式为{pr,pr}或{pr,cr},那么,tp=pr,to=t1/ps1+t2/ps2,st=st1+t2/ps2,ps=1;
在序列模式中,如果模式为{c,p}或{c,c},那么,tp=p或c,to=t1+t2,st=(st1+t2)/ps2,ps=ps1ps2;如果序列模式为{c,pr}或{c,cr},tp=p或c,to=t1+t2/ps2,st=st1+t2/ps2,ps=ps1;如果序列模式为{cr,p}或{cr,c},tp=p或c,to=t1/ps1+t2,st=(st1+t2)/ps2,ps=ps2;如果序列模式为{cr,pr}或{cr,cr},tp=pr或cr,to=t1/ps1+t2/ps2,st=st1+t2/ps2,ps=1;
如果序列模式为{c,p}或{c,c},执行一次该模式,如果WS1执行失败,那么模式执行失败,时间为t1;如果WS1成功执行完成,WS2执行一次,如果WS2的执行失败,模式失败,如果WS2的成功执行完成,模式成功执行完成,时间为t1+t2;所以在t1+t2时间内,我们可以判断模式是否成功执行完成,那么to=t1+t2;
如果WS1执行失败,那么模式执行失败,同样,重复执行WS1,直到WS1成功执行完成;假设WS1的成功执行完成的时间为st1,WS2的执行失败会导致WS1被补偿,并且回滚到模式的起点位置,那么也会导致模式执行失败;同样,重复执行WS2,直到WS2执行成功完成。WS2每次失败都会导致WS1和WS2的重新执行一次,直到WS1和WS2都执行成功。那么服务WS2经过k次执行后成功完成的时间为:k(st1+t2),概率为:
P(X=k)=(1-ps2)k-1ps2
那么成功完成时间即数学期望为
WS1和WS2的成功执行完成的概率分别是ps1和ps2,那么模式成功执行完成概率为ps=ps1ps2;如果模式为{c,p},tp=p;如果模式为{c,c},tp=c;
如果序列模式为{c,pr}或{c,cr},那么WS2经过有限次数重试一定能成功完成,WS1和WS2的成功执行完成时间分别是st1和t2/ps2,所以st=st1+t2/ps2;to=t1+t2/ps2,ps=1;
如果序列模式为{cr,p}或{cr,c},执行一次该模式,WS1经过有限次重试必定成功完成,WS1的成功执行时间为st1=t1/ps1;WS2执行一次,根据WS2的执行结果,模式或者执行失败或者成功执行完成,时间为t1/ps1+t2;所以在t1/ps1+t2时间内,我们可以判断模式是否成功执行完成,那么to=t1/ps1+t2;st=(st1+t2)/ps2;WS1和WS2的成功执行完成的概率分别是1和ps2,那么,ps=ps2;如果模式为{cr,p},tp=p;如果模式为{cr,c},tp=c。
(2)并行模式时间性能计算方法
并行模式用来定义组合服务中组件服务没有严格执行顺序、必须同时进行的组合服务;只有所有并行服务都成功执行完成时,这个组合服务才能成功执行完成;如果一些服务成功执行完成,另一些服务执行失败,那么需要利用事务机制对执行失败的服务进行处理;这里,max{x,y}表示x和y两者的最大值;min{x,y}表示x和y两者的最小值;假设在执行并行模式服务时,优先级为从上往下执行;首先考虑两个服务组成的并行模式;
在并行模式中,如果服务WS1的事务性为p,一旦WS1成功执行完成,它产生的影响不能被撤销,因此服务WS2必须确保一定成功执行完成,即WS2包含r的事务性;另一方面,一旦WS1执行失败,WS2必须能提供补偿策略,所以WS2包含c的事务性,那么WS2的事务性只能为cr;
当WS1和WS2同时执行时,由于WS2的事务性为cr,WS2能经过有限次数的调用确保成功执行完成,时间为t2/ps2;WS1执行一次的时间为t1;那么在时间max{t1,t2/ps2}内,并行模式可以确定是否成功执行完成;所以,to=max{t1,t2/ps2};WS1的失败会导致WS2被补偿,使得并行模式执行失败,所以我们重复执行该模式直到成功执行完成;WS1经过k次执行后成功完成的概率为:
P(X=k)=(1-ps1)k-1ps1
那么,成功执行时间为:
并行模式的执行成功完成的概率为WS1和WS2执行成功完成概率乘积,而WS2的执行成功完成概率为1,那么,ps=ps1,tp=p;
在并行模式中,如果一个服务WS1的事务性为pr,WS1经过有限次数的调用,一定能成功执行完成,而且成功完成后,其影响就不能被撤销;所以另一个服务WS2必须确保成功执行完成,即事务性必须包含r,那么服务WS2的事务性为pr或cr;
在并行模式中,如果模式为{pr,pr}或{pr,cr},那么,tp=pr,to=max{t1/ps1,t2/ps2},st=max{t1/ps1,t2/ps2},ps=1;
由于WS1和WS2的事务性都包含r,所以它们都能经过有限次重试确保成功执行完成,且执行一次的时间分别为t1/ps1和t2/ps2,而且执行一次的时间就是成功执行完成的时间,成功执行完成的概率都为1;所以在并行模式中,to=max{t1/ps1,t2/ps2},st=max{t1/ps1,t2/ps2},ps=1,tp=pr;
在并行模式中,如果一个服务WS1的事务性为c,那么WS1可能失败;所以另一个服务WS2必须是可补偿的;即WS2的是事务性包含c,那么,WS2的事务性可以为c或cr;
在并行模式中,如果模式为为{c,cr},tp=c,to=max{t1,t2/ps2},st=max{t1,t2/ps2}/ps1,ps=ps1;如果并行模式为{c,c},tp=c,to=max{t1,t2},st=max{t1,t2}/min{ps1,ps2},ps=ps1ps2;
如果并行模式为{c,c},由于WS1和WS2分别执行一次的时间为t1和t2,故to=max{t1,t2},由于WS1和WS2都能提供补偿策略,当为某一个服务提供补偿策略后,每次重新执行一次并行模式,实际上两个服务都被补偿了一次;那么补偿次数取决于需要被补偿次数更多的服务,也就是成功执行完成概率更小的服务;故st=max{t1,t2}/min{ps1,ps2};WS1和WS2成功执行完成的概率分别为ps1和ps2,故ps=ps1ps2;tp=c;
在并行模式中,如果一个服务WS1的事务性为cr,经过有限调用WS1能够确保成功完成;并且,当WS2执行失败,WS1是可补偿的;所以另一个服务的WS2可以是任何事务性的服务;
如果并行模式为{cr,cr},那么,tp=cr,to=max{t1/ps1,t2/ps2},st=max{t1/ps1,t2/ps2},ps=1。
(3)选择模式时间性能计算方法
一种是用来定义彼此之间相互制约与排斥关系的分支服务,这类分支服务往往根据具体的执行情况从多个分支选择一个分支执行,选择模式只有一个服务可以被执行;所以可以归结为序列模式的讨论;另外一种选择模式为任选其一的选择模式,分支服务是可以替代的,当某个分支执行失败后,选择另外一个分支替代,直到获得成功的分支,或者所有分支都失败,然后进行补偿;
假设在执行选择模式服务时,优先级为从上往下执行;首先考虑两个服务组成的选择模式;
在选择模式中,两个服务都赋予相同事务特性的服务,那么模式的事务性为组件服务相应的事务性,to=(t1+t2),st=(t1+t2)/(ps1+ps2-2ps1ps2),ps=ps1+ps2-2ps1ps2;
在选择模式中,由于被选择服务都是完成同样功能的服务,选择模式中服务赋予服务的事务性是对等的,在选择模式中,服务只能赋予相同事务性的服务才能满足选择模式的物理含义;所以,两个服务赋予相同事务性的服务;在选择模式中,如果组件服务的事务性为p或c,那么如果WS1成功执行完成,时间为t1,如果WS1执行失败,WS2成功执行完成,时间为t1+t2,如果WS1和WS2都失败,并行模式失败,时间为t1+t2;那么在t1+t2,内可以判断并行模式是否成功执行完成,故to=(t1+t2);由于选择模式只有一个服务进入事务组合服务中,故不考虑单独服务的ST;第一个服务失败,第二个服务成功的概率为(1-ps1)ps2,事务组合服务成功的概率为ps1+(1-ps1)ps2=ps1+ps2-ps1ps2,TCWS的事务性为p或c;如在选择模式中,如果组件服务的事务性为pr或cr,模式只需要执行第一个组件服务就可以使得模式成功执行完成,st=to=t1/ps1,ps=1。
所述第三步的具体内容如下:
本方法基于事务和QoS的服务选择方法,提出两个QoS指标:成功完成时间和执行价格,成功完成时间根据时间性能分析方法获得,执行价格根据组合服务每个组件服务的执行价格之和获得;然后对成功完成时间和执行价格进行加权处理,以获得事务组合服务的QoS分数值,并作为对事务组合服务进行选择的标准。
所述QoS指标还包括信誉、可获得性。
本发明提供的技术方案选择准确度好,且具有较好的可行性和有效性。
附图说明
为了更清楚地说明本发明实施例或现有技术中的技术方案,下面将对实施例或现有技术描述中所需要使用的附图作一简单地介绍,显而易见地,下面描述中的附图是本发明的一些实施例,对于本领域普通技术人员来讲,在不付出创造性劳动性的前提下,还可以根据这些附图获得其他的附图。
图1为本发明组合模式为序列模式的示意图;
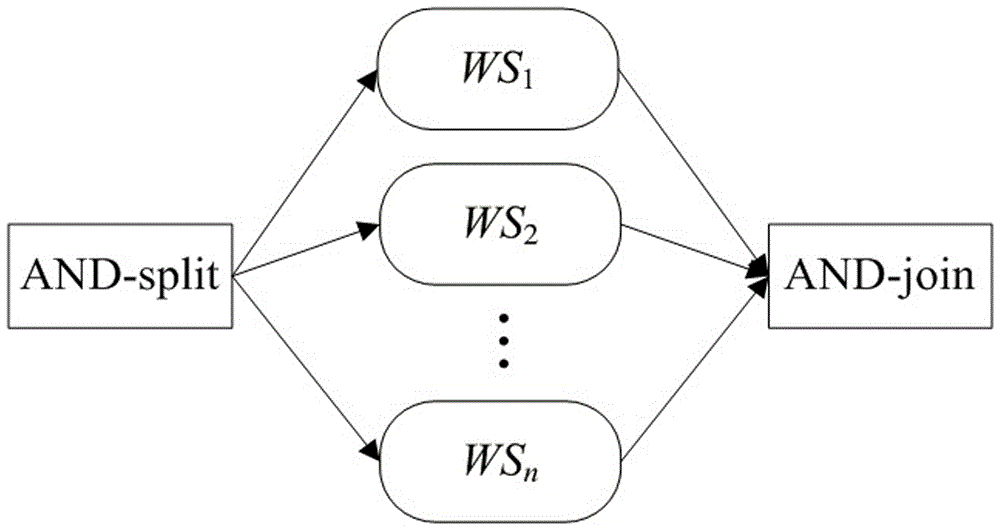
图2为本发明组合模式为并列模式的示意图;
图3为本发明组合模式为选择模式的示意图。
具体实施方式
实现本发明的技术方案为:首先对Web服务赋予事务性,然后分析具有事务性要求服务的组合问题,其次分析具有事务属性组合服务的性能问题,最后,根据事务性组合服务的性能比较,提出基于事务和QoS的组合Web服务选择方法。具体包括以下步骤:
第一步、在进行当前组件服务的选择时,根据前面已经选择合适组件服务的事务特点,并按照事务组合服务的规则要求,获得满足事务性要求的候选组件服务。
第二步、对每个候选组件服务进行性能评估,评估考虑Web服务的QoS和事务性要求。
第三步、重复以上过程,直到获得一个满足要求的组合服务。
第一步和第二步中事务组合服务方法及性能评估的具体内容如下:
在通常的服务选择方法,性能评估都是基于所有组件服务的QoS进行分析,而本发明基于事务性和QoS,把两者相结合获取到基于事务的组合服务选择方法。
在基于事务的组合服务选择过程中,当一些功能性相似的候选组件服务可以被获得时,它们的非功能性要求QoS就变得非常重要。由于QoS能够很好地反映用户的需求,所以它是目前最常用的非功能性指标,本发明考虑Web服务ws下面三个QoS指标:
(1)执行价格(Execution price,EP):请求者调用服务ws所需要的花费,表示为qep(ws)。
(2)执行时间(Execution time,ET):服务ws执行一次所需要的时间,表示为qet(ws)。本文认为服务执行一次的时间是相同的,并且在相同的时间内,服务执行一次可能失败,也可能成功完成。
(3)成功完成概率(Probability of Success,PS):服务ws成功完成用户请求的概率,表示为qps(ws)。
其中,执行时间需要考虑组合服务的事务性带来的变化,分析过程如下:
(1)一个服务具有可补偿性,那么它能提供补偿策略来撤销该服务的影响,用符号“c”表示。
(2)一个服务具有可不断重试性,那么它能被重试,并且通过足够次数的重试达到最终成功,用符号“r”表示。
(3)一个服务具有中心点特性,那么它一旦执行成功,它的影响永远存在,而且不能被撤销,如果它执行失败,没有任何影响,用符号“p”表示。
由于网络环境的动态性,不确定性和开放性,来自不同组织的组件服务往往会调用失败,假设一个Web服务成功执行的概率为ps。服务执行一次的时间为t,那么在时间t内一个Web服务或者成功执行,或者执行失败。服务在前n-1次执行都失败,第n次执行成功的概率符合几何分布,概率函数为:
P(X=n)=(1-ps)n-1ps
X表示服务第几次执行,那么数学期望值为:
几何分布的数学期望反应的就是成功的平均执行次数,即成功执行的平均次数为1/ps,服务执行一次的时间为t,那么,成功执行的平均时间st为:
st=t/ps
通常,组合服务由基本组合模式构成,因此为了考虑事务组合服务的时间性能,我们需要分析基本组合模式的时间性能。这里,我们讨论四种基本的组合模式,分别是:序列,并行,选择和循环模式。并且服务组合由工作流模型来描述。TP表示事务性,TO表示一次执行时间,ST表示成功执行时间,PS表示成功执行概率。tp、to、st和ps表示组合服务相应概念的具体值。为了简单考虑,模式中每次只有一个组件服务执行失败。
(1)序列模式时间性能分析
序列模式用来定义组合服务由一系列按固定顺序执行的组件服,由n个组件服务组成的序列模式如图1所示。在序列模式中,组件服务从左到右执行,当且仅当前面的组件服务成功执行完成后,后面的组件服务才能开始执行。如果有组件服务执行失败,将利用事务机制处理失败。前i个组件服务成功执行时间为sti,组件服务WSi执行一次的时间为ti,服务WSi成功执行的概率为psi。
首先考虑两个服务组成的组合序列模式,n个服务组成的组合模式可以看作前n-1服务的组合服务和第n个服务的组合。
在序列模式中,如果第一个服务WS1被赋予的事务特性为p或pr,根据定义4.3和4.6,WS1一旦成功完成,就不能被撤销,因此第二个服务WS2必须保证一定成功完成,即WS2必须包括r的事务性,所以WS2赋予事务性为pr或cr。{tp1,tp2}表示模式中从左到右或者从上到下的两个服务的事务性。
如果序列模式为{p,pr}或{p,cr},执行一次该模式,如果WS1执行失败,那么模式执行失败,时间为t1。如果WS1成功执行完成,由于WS2经过有限次数重试必定成功完成,所以模式成功执行完成,时间为t1+t2/ps2。那么在t1+t2/ps2时间内,我们可以判断该模式是否成功执行完成,故to=t1+t2/ps2。WS1成功执行完成概率为ps1,由于WS2经过有限次数重试必定成功完成,在模式执行过程中,我们认为事务性包含r的服务执行完成概率为1,即WS2成功执行完成概率为1。所以该组合服务的成功执行概率为ps=ps1,组合服务的事务性为p。
如果WS1执行失败,那么模式执行失败,为了分析该模式的成功完成时间,WS1将重复执行,直到WS1成功执行完成,那么模式成功完成。假设WS1的成功执行完成时间为st1(如果WS1为原子服务,st1=t1/ps1,如果WS1为组合服务,st1为组合服务的成功完成时间),由于WS2经过有限次数重试必定成功完成,那么st=st1+t2/ps2。
如果序列模式为{pr,pr}或{pr,cr},执行一次模式,WS1和WS2都经过有限次数重试必定成功完成,那么to=t1/ps1+t2/ps2,执行一次时间也为成功执行完成时间,故st=st1+t2/ps。WS1和WS2成功执行完成概率都为1,那么模式成功执行的概率为ps=1,组合服务的事务性为pr。
在序列模式中,如果第一个服务WS1赋予的事务性是c或cr,那么如果第二个服务WS2执行失败,第一个服务执行可以被撤销,所以第二个服务WS2可以赋予任何事务性。
在序列模式中,如果模式为{p,pr}或{p,cr},那么,tp=p,to=t1+t2/ps2,st=st1+t2/ps2,ps=ps1。如果序列模式为{pr,pr}或{pr,cr},那么,tp=pr,to=t1/ps1+t2/ps2,st=st1+t2/ps2,ps=1。
在序列模式中,如果模式为{c,p}或{c,c},那么,tp=p或c,to=t1+t2,st=(st1+t2)/ps2,ps=ps1ps2。如果序列模式为{c,pr}或{c,cr},tp=p或c,to=t1+t2/ps2,st=st1+t2/ps2,ps=ps1。如果序列模式为{cr,p}或{cr,c},tp=p或c,to=t1/ps1+t2,st=(st1+t2)/ps2,ps=ps2。如果序列模式为{cr,pr}或{cr,cr},tp=pr或cr,to=t1/ps1+t2/ps2,st=st1+t2/ps2,ps=1。
如果序列模式为{c,p}或{c,c},执行一次该模式,如果WS1执行失败,那么模式执行失败,时间为t1。如果WS1成功执行完成,WS2执行一次,如果WS2的执行失败,模式失败,如果WS2的成功执行完成,模式成功执行完成,时间为t1+t2。所以在t1+t2时间内,我们可以判断模式是否成功执行完成,那么to=t1+t2。
如果WS1执行失败,那么模式执行失败,同样,重复执行WS1,直到WS1成功执行完成。假设WS1的成功执行完成的时间为st1,WS2的执行失败会导致WS1被补偿,并且回滚到模式的起点位置,那么也会导致模式执行失败。同样,重复执行WS2,直到WS2执行成功完成。WS2每次失败都会导致WS1和WS2的重新执行一次,直到WS1和WS2都执行成功。那么服务WS2经过k次执行后成功完成(即经过k-1次执行失败后成功)的时间为:k(st1+t2),概率为:
P(X=k)=(1-ps2)k-1ps2
那么成功完成时间即数学期望为
WS1和WS2的成功执行完成的概率分别是ps1和ps2,那么模式成功执行完成概率为ps=ps1ps2。如果模式为{c,p},tp=p。如果模式为{c,c},tp=c。
如果序列模式为{c,pr}或{c,cr},那么WS2经过有限次数重试一定能成功完成(定义4.3),WS1和WS2的成功执行完成时间分别是st1和t2/ps2,所以st=st1+t2/ps2。类似定理4.1中序列模式为{p,pr}和{p,cr}的证明,to=t1+t2/ps2,ps=1。
如果序列模式为{cr,p}或{cr,c},执行一次该模式,WS1经过有限次重试必定成功完成(定义4.3),WS1的成功执行时间为st1=t1/ps1(虽然和以上讨论事务性为c的WS1成功执行时间相同,但是原因不同)。WS2执行一次,根据WS2的执行结果,模式或者执行失败或者成功执行完成,时间为t1/ps1+t2。所以在t1/ps1+t2时间内,我们可以判断模式是否成功执行完成,那么to=t1/ps1+t2。类似序列模式为{c,p}或{c,c}的证明过程,st=(st1+t2)/ps2。WS1和WS2的成功执行完成的概率分别是1和ps2,那么,ps=ps2。如果模式为{cr,p},tp=p。如果模式为{cr,c},tp=c。
如果序列模式为{cr,pr/cr},类似序列模式{pr,pr/cr}的说明。
表1序列模式事务性赋值和时间性能分析
(2)并行模式时间性能计算方法
并行模式用来定义组合服务中组件服务没有严格执行顺序、必须同时进行的组合服务。其模式如图2所示。只有所有并行服务都成功执行完成时,这个组合服务才能成功执行完成。如果一些服务成功执行完成,另一些服务执行失败,那么需要利用事务机制对执行失败的服务进行处理。这里,max{x,y}表示x和y两者的最大值。min{x,y}表示x和y两者的最小值。假设在执行并行模式服务时,优先级为从上往下执行。我们首先考虑两个服务组成的并行模式。
在并行模式中,如果服务WS1的事务性为p,一旦WS1成功执行完成,它产生的影响不能被撤销,因此服务WS2必须确保一定成功执行完成,即WS2包含r的事务性。另一方面,一旦WS1执行失败,WS2必须能提供补偿策略,所以WS2包含c的事务性,那么WS2的事务性只能为cr。
当WS1和WS2同时执行时,由于WS2的事务性为cr,WS2能经过有限次数的调用确保成功执行完成,时间为t2/ps2。WS1执行一次的时间为t1。那么在时间max{t1,t2/ps2}内,并行模式可以确定是否成功执行完成。所以,to=max{t1,t2/ps2}。WS1的失败会导致WS2被补偿,使得并行模式执行失败,所以我们重复执行该模式直到成功执行完成。WS1经过k次执行后成功完成的概率为:
P(X=k)=(1-ps1)k-1ps1
那么,成功执行时间为:
并行模式的执行成功完成的概率为WS1和WS2执行成功完成概率乘积,而WS2的执行成功完成概率为1,那么,ps=ps1,tp=p。
在并行模式中,如果一个服务WS1的事务性为pr,WS1经过有限次数的调用,一定能成功执行完成,而且成功完成后,其影响就不能被撤销(定义4.3)。所以另一个服务WS2必须确保成功执行完成,即事务性必须包含r,那么服务WS2的事务性为pr或cr。
在并行模式中,如果模式为{pr,pr}或{pr,cr},那么,tp=pr,to=max{t1/ps1,t2/ps2},st=max{t1/ps1,t2/ps2},ps=1。
由于WS1和WS2的事务性都包含r,所以它们都能经过有限次重试确保成功执行完成,且执行一次的时间分别为t1/ps1和t2/ps2,而且执行一次的时间就是成功执行完成的时间,成功执行完成的概率都为1。所以在并行模式中,to=max{t1/ps1,t2/ps2},st=max{t1/ps1,t2/ps2},ps=1,tp=pr。
在并行模式中,如果一个服务WS1的事务性为c,那么WS1可能失败。所以另一个服务WS2必须是可补偿的。即WS2的是事务性包含c,那么,WS2的事务性可以为c或cr[64]。
在并行模式中,如果模式为为{c,cr},tp=c,to=max{t1,t2/ps2},st=max{t1,t2/ps2}/ps1,ps=ps1。如果并行模式为{c,c},tp=c,to=max{t1,t2},st=max{t1,t2}/min{ps1,ps2},ps=ps1ps2。
如果并行模式为{c,cr},证明类似,这里不再重述。如果并行模式为{c,c},由于WS1和WS2分别执行一次的时间为t1和t2,故to=max{t1,t2},由于WS1和WS2都能提供补偿策略,当为某一个服务(该服务执行失败)提供补偿策略后,每次重新执行一次并行模式,实际上两个服务都被补偿了一次。那么补偿次数取决于需要被补偿次数更多的服务,也就是成功执行完成概率更小的服务。故st=max{t1,t2}/min{ps1,ps2}。WS1和WS2成功执行完成的概率分别为ps1和ps2,故ps=ps1ps2。根据定义4.4,tp=c。
在并行模式中,如果一个服务WS1的事务性为cr,根据定义4.2,经过有限调用WS1能够确保成功完成。并且,当WS2执行失败,WS1是可补偿的。所以另一个服务的WS2可以是任何事务性的服务。
如果并行模式为{cr,cr},那么,tp=cr,to=max{t1/ps1,t2/ps2},st=max{t1/ps1,t2/ps2},ps=1。
由于并行模式中服务为对称的,并行模式{cr,p},{cr,c}和{cr,pr}的公式可以参考定理4.3,4.4,4.5中给出的相应公式,这里不再复述。并行模式{cr,cr}的公式可以参考定理4.3中的模式{pr,pr}的证明。
基于两个服务的并行模式的事务性赋值和时间性能分析如表所示。
表2并行模式事务性赋值和时间性能分析
(3)选择模式时间性能分析
在本节中,我们考虑两种选择模式:一种是用来定义彼此之间相互制约与排斥关系的分支服务,这类分支服务往往根据具体的执行情况从多个分支选择一个分支执行,选择模式只有一个服务可以被执行。所以可以归结为序列模式的讨论。另外一种选择模式为任选其一的选择模式,分支服务是可以替代的,当某个分支执行失败后,选择另外一个分支替代,直到获得成功的分支,或者所有分支都失败,然后进行补偿,如图3所示。我们主要考虑第二种选择模式的时间性能分析。
假设在执行选择模式服务时,优先级为从上往下执行。我们首先考虑两个服务组成的选择模式。
在选择模式中,两个服务都赋予相同事务特性的服务,那么模式的事务性为组件服务相应的事务性,to=(t1+t2),st=(t1+t2)/(ps1+ps2-2ps1ps2),ps=ps1+ps2-2ps1ps2。
在选择模式中,由于被选择服务都是完成同样功能的服务,所以,在本文中,为了简单起见,我们认为选择模式中服务赋予服务的事务性是对等的,也就是说,在选择模式中,服务只能赋予相同事务性的服务才能满足选择模式的物理含义。所以,两个服务赋予相同事务性的服务。在选择模式中,如果组件服务的事务性为p或c,那么如果WS1成功执行完成,时间为t1,如果WS1执行失败,WS2成功执行完成,时间为t1+t2,如果WS1和WS2都失败,并行模式失败,时间为t1+t2。那么在t1+t2,内可以判断并行模式是否成功执行完成,故to=(t1+t2)。由于选择模式只有一个服务进入事务组合服务中,故不考虑单独服务的ST。第一个服务成功,模式成功,概率为,第一个服务失败,第二个服务成功的概率为(1-ps1)ps2,事务组合服务成功的概率为ps1+(1-ps1)ps2=ps1+ps2-ps1ps2,TCWS的事务性为p或c。组合服务选择模式的事务性赋值和时间性能分析如表3所示。如在选择模式中,如果组件服务的事务性为pr或cr,模式只需要执行第一个组件服务就可以使得模式成功执行完成,st=to=t1/ps1,ps=1。
表3选择模式事务性赋值和时间性能分析
第三步中事务组合服务选择方法的具体内容如下:
本节主要研究基于事务和QoS的服务选择方法,并且考虑两个QoS指标:成功完成时间和执行价格,前者可以根据前面的时间性能分析算法获得,后者可以根据组合服务每个组件服务的执行价格之和获得。然后对两者进行加权处理,以获得事务组合服务的QoS分数值,并作为对事务组合服务进行选择的标准。由于本文使用的是标准的QoS属性,所以其它的QoS指标,比如:信誉,可获得性等,可以通过同样的方式扩展考虑。
- 还没有人留言评论。精彩留言会获得点赞!