一种基于网络好友的根密钥管理方法及装置与流程

本发明涉及密钥管理领域，尤其是一种基于网络好友的根密钥管理方法及装置。

背景技术：

传统的根密钥一般主要有三种保护手段：(1)使用专用硬件存储，安全性高，但成本也较高，丢失后无法恢复；(2)通过邮箱或者第三方进行存储，使用不方便，且安全性极差；(3)通过口令加密存储，每次使用时通过口令解密获取，口令忘记后，将无法进行恢复，且口令一般随机性较低，长度较短，容易被暴力破解。

技术实现要素：

本发明所要解决的技术问题是：针对现有技术存在的问题，提供一种基于网络好友的根密钥管理方法及装置。本专利主要针对于目前根密钥保护难度大，使用不方便，易忘记或者丢失的问题展开研究，通过使用网络好友关系，将用户的口令通过Shamir门限方案分解成若干部分，继而存储在不同的好友处，如果用户一旦忘记根密钥，继而通过视频、语音等方式便可以通过部分好友恢复成用户的根密钥，确保根密钥的安全性。

本发明采用的技术方案如下：

一种基于网络好友的根密钥管理方法包括：

根密钥生成步骤：用户生成本地数据加密的根密钥key；通过shamir门线方案，随机选取n个随机数xi，随机选取t-1次多项式f(xi)，设置f(0)＝key，然后生成相应的部分根密钥数据(xi,yi)；n≥i≥1；

根密钥分发步骤：用户选取n个好友，使用好友的公钥pk加密部分根密钥数据(x_i,y_i)，并将加密后的数据发送给该好友；该好友接收到消息后解密该信息，并将其加密存储；

根密钥恢复步骤：当用户忘记自己的根密钥,进而导致根密钥保护的公钥私钥丢失，用户新生成一对公私钥(pk1,sk1)；通过公私钥(pk1,sk1)与之前存储部分根密钥数据的好友进行数据交互，获取t个部分根密钥数据(x_i,y_i)，使用Shamir门限方案的秘密重构公式恢复根密钥key。

进一步的,所述根密钥恢复步骤具体包括：

用户输入包含所需要恢复时间的本地认证信息，用户选取m个持有用户部分根密钥的好友，使用m个好友的公钥分别加密认证信息以及公钥pk1，得到m个密文信息；用户将m个密文信息对应发送给m个好友；

m个好友分别获取密文信息,并通过该好友对应的私钥解密密文信息,得到认证信息以及用户公钥pk1,好友判断认证信息是否属实，若属实，则使用密文信息中的公钥pk1加密该好友存储的部分根密钥数据(x_i,y_i)，得到加密密文后发送给用户；否则，退出；

用户接收到好友返回的加密密文后,通过私钥sk1解密获取部分根密钥数据(x_i,y_i)；判断收到的部分根密钥数据个数是否大于或等于t个，如果满足则基于t个部分根密钥数据(x_i,y_i)使用Shamir门限方案的秘密重构公式恢复根密钥key，否则退出；n≥m≥t。

进一步的,所述认证信息指的是好友与用户能进行身份认证的信息。

进一步的，所述获取t个部分根密钥数据(x_i,y_i)，使用Shamir门限方案的秘密重构公式恢复根密钥key具体过程是：

假设有t个点(x₁,y₁),(x₂,y₂),…,(x_t,y_t)，可求根密钥key为：

一种基于网络好友的根密钥管理装置包括:

根密钥生成模块：用户生成本地数据加密的根密钥key；通过shamir门线方案，随机选取n个随机数xi，随机选取t-1次多项式f(xi)，设置f(0)＝key，然后生成相应的部分根密钥数据(xi,yi)；n≥i≥1；

根密钥分发模块：用户选取n个好友，使用好友的公钥pk加密部分根密钥数据(x_i,y_i)，并将加密后的数据发送给该好友；该好友接收到消息后解密该信息，并将其加密存储；

根密钥恢复模块：当用户忘记自己的根密钥,进而导致根密钥保护的公钥私钥丢失，用户新生成一对公私钥(pk1,sk1)；通过公私钥(pk1,sk1)与之前存储部分根密钥数据的好友进行数据交互，获取t个部分根密钥数据(x_i,y_i)，使用Shamir门限方案的秘密重构公式恢复根密钥key。

进一步的,所述根密钥恢复模块具体包括：

用户输入包含所需要恢复时间的本地认证信息，用户选取m个持有用户部分根密钥的好友，使用m个好友的公钥分别加密认证信息以及公钥pk1，得到m个密文信息；用户将m个密文信息对应发送给m个好友；

m个好友分别获取密文信息,并通过该好友对应的私钥解密密文信息,得到认证信息以及用户公钥pk1,好友判断认证信息是否属实，若属实，则使用密文信息中的公钥pk1加密该好友存储的部分根密钥数据(x_i,y_i)，得到加密密文后发送给用户；否则，退出；

用户接收到好友返回的加密密文后,通过私钥sk1解密获取部分根密钥数据(x_i,y_i)；判断收到的部分根密钥数据个数是否大于或等于t个，如果满足则基于t个部分根密钥数据(x_i,y_i)使用Shamir门限方案的秘密重构公式恢复根密钥key，否则退出；n≥m≥t。

进一步的,所述认证信息指的是好友与用户能进行身份认证的信息。

进一步的，所述获取t个部分根密钥数据(x_i,y_i)，使用Shamir门限方案的秘密重构公式恢复根密钥key具体过程是：

假设有t个点(x₁,y₁),(x₂,y₂),…,(x_t,y_t)，可求根密钥key为：

综上所述，由于采用了上述技术方案，本发明的有益效果是：

(1)通过网络好友关系实现用户根密钥的分布式管理保存，实现根密钥的安全存储，较传统的方案安全高；

(2)通过网络的方式保护便于密钥的恢复，用户忘记根密钥时，也可以通过众多网络好友的认证继而恢复根密钥，简单、快捷、方便；

(3)根密钥的恢复只需要大于门限值的部分秘密便可以恢复，并不需要全员的参与。

附图说明

本发明将通过例子并参照附图的方式说明，其中：

图1是根密钥生成示意图。

图2是根密钥分发示意图。

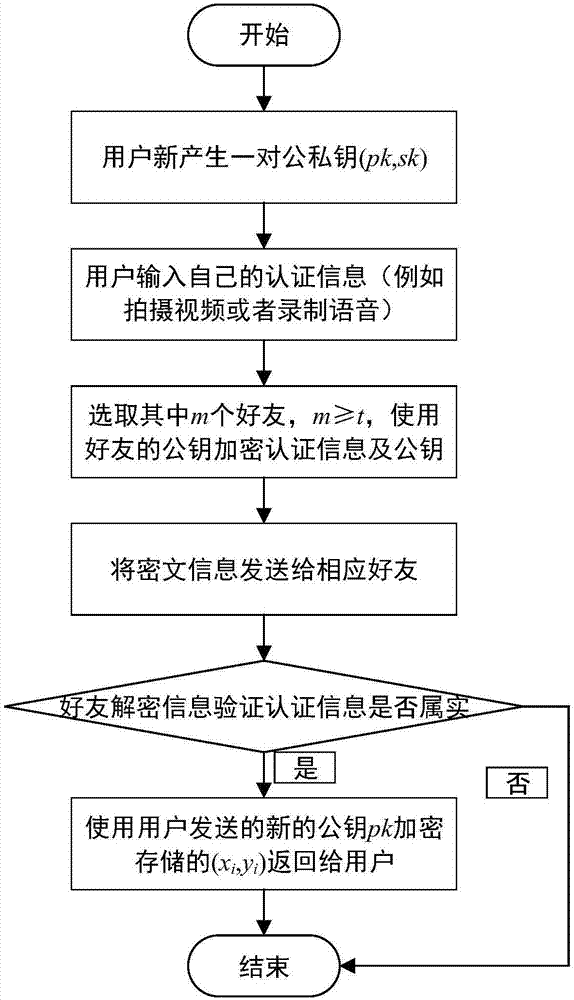
图3是根密钥恢复示意图。

具体实施方式

本说明书中公开的所有特征，或公开的所有方法或过程中的步骤，除了互相排斥的特征和/或步骤以外，均可以以任何方式组合。

本说明书中公开的任一特征，除非特别叙述，均可被其他等效或具有类似目的的替代特征加以替换。即，除非特别叙述，每个特征只是一系列等效或类似特征中的一个例子而已。

本专利提出了一种基于网络好友的根密钥管理方法，通过社交网络关系实现根密钥的分布式管理恢复，首先通过Shamir(t,n)门限方案将根密钥分解成n份，得到t份便可以恢复出根密钥；继而将n份部分密钥分别发送给n个不同的好友进行存储；当用户忘记密钥时，通过产生新的公钥及自己的视频、语音等信息发送给n个好友；好友对相应信息进行验证之后，如果确认属实，便会使用新的公钥加密用户的部分密钥发送给用户；用户获取到t个部分密钥时，即可恢复出相应的根密钥。

本专利基于的Shamir(t,n)门限方案介绍如下：

(1)系统参数

假定n是参与者P的数目，t是门限值，p是一个大素数，满足p>n且大于秘密s可能的最大取值，秘密空间和份额空间均为有限域GF(p)。

(2)秘密分发

1)用户随机选择一个GF(p)上的t-1次多项式f(x)，使得f(0)＝s；

2)用户在Zp中选择n个互不相同的非零元素x₁,x₂，…，x_n，计算y_i＝f(x_i)，其中0≤i≤n；

3)将(x_i,y_i)发送给秘密持有者，其中x_i是公开的，y_i只有秘密持有者保有。

(3)秘密重构

给定任何k个点，假设有前k个点(x₁,y₁),(x₂,y₂),…,(x_k,y_k)，可求的秘密为

除Shamir门限方案之外，本专利使用的所有公钥加密算法均使用国家商用密码算法标准SM2公钥密码算法。

本专利所描述的方法共包含三个部分：(1)根密钥生成及分发；(2)根密钥恢复验证；(3)根密钥恢复。

初始系统描述：网络应用(例如聊天软件)存在较多的用户，每一个用户均持有一对公私钥(pk,sk)用于消息传递和一个根密钥用于数据加密，每一个用户均拥有自己的好友，部分好友是可信赖的(例如实际生活中的亲戚、朋友、同事)。

(1)根密钥生成及分发

第一步：用户生成自己数据加密的根密钥key；

第二步：用户通过Shamir门限方案，选取相应的系统参数，继而随机选取t-1次多项式，使得f(0)＝key；

第三步：用户根据系统参数随机选取n个随机数x_i，并生成相应的点(x_i,y_i)；

第四步：用户选取n个好友，使用相应好友的公钥pk加密相应的点(x_i,y_i)，将其通过应用系统发送给该好友；

第五步：该好友接收到消息后解密该信息，并将其加密存储。

(2)根密钥恢复验证

假设用户忘记了自己的根密钥，相应通过根密钥保护的自己的公钥私钥均已丢失，继而希望通过好友对根密钥进行恢复。

第一步：用户新产生一对公私钥(pk,sk)；

第二步：用户输入自己的认证信息，为了安全性考虑，该信息应包含所需要恢复的时间，防止重放攻击，认证信息可以是视频或者语音等其他有关身份的信息；

第三步：用户选取m个持有自己部分根密钥的好友，其中m≥t，使用该好友的公钥加密认证信息及新产生的公钥pk；

第四步：将密文信息发送给选取的好友；

第五步：好友获取后判断认证信息是否属实，是则执行第六部，否则退出；

第六步：信息属实，则使用接收到的公钥pk加密存储的部分秘密(x_i,y_i)，将密文发送给请求用户。

(3)根密钥恢复

第一步：用户使用在(2)中新生成的私钥sk解密获取(x_i,y_i)；

第二步：判断收到的部分秘密是否大于或等于t个，如果满足则执行第三步，否则退出；

第三步：使用Shamir门限方案的秘密重构公式恢复根密钥key。

本发明并不局限于前述的具体实施方式。本发明扩展到任何在本说明书中披露的新特征或任何新的组合，以及披露的任一新的方法或过程的步骤或任何新的组合。