密码S盒评估新方法与流程

本发明涉及信息安全领域，具体是一种密码S盒评估新方法。

背景技术：

密码S盒是对称密码算法的关键部件，其代数性质和代数结构很大程度上决定了整个密码算法的安全强度。关于S盒的代数性质研究较多，目前最常见的S盒度量指标列举如下：非线性度、差分均匀性、平衡性、扩散性和可逆性、代数次数及项数分布、正交性、相关免疫性。对于代数性质较好的S盒，为了抵抗线性密码分析，一般都会具有较高的非线性度；为了抵抗差分密码分析，需要较大的差分均匀性；为了抵抗代数攻击和立方攻击，需要较高的代数次数，并且不同的代数次数的项数分布较均匀。

1991年，Biham和Shamir在密码分析体制中提出了差分攻击的概念。从那之后，学者在设计S盒时开始考虑其抵抗差分攻击的能力。Dawson和Tavares进一步扩展了S盒的安全性指标，详细说明了设计S盒怎样很好地抵抗差分攻击。2005年，Chen等提出了关于S盒的偏差检测。他们利用这种新的统计测试性能指标对Rijndael和Crypton结构中的S盒进行测试，得到在这种新指标下Rijndael的安全性能优于Crypton。2009年，LIU和XIAO提出k-k独立的概念，给出了S盒和组件函数线性组合的反演公式，这个工具在一定程度下反映了S盒的安全性。2013年，Boura等根据布尔函数中的Maiorana-McFarland构造理论提出了一个针对非线性S盒新的度量指标：(v,w)线性。这个指标可以反映S盒线性关系的扩散能力。他们利用这个新指标优化了针对Hamsi算法的Fuhr攻击。

利用这些关于S盒的安全性检测技术，对于设计性质较好的S盒具有很大的帮助。但是，这些方法一般都是在代数性质上对S盒进行评估，而使用当今的S盒设计方法得到的S盒是否存在代数结构上的缺陷还不为人知，所以，迫切需要一种可以在代数结构上对S盒进行评估的方法。

技术实现要素：

针对上述不足，本发明所要解决的技术问题是提供一种在代数结构上对密码S盒进行评估的新方法，引入S盒的局部线性关系分解以及局部二次关系分解概念，深入研究了S盒的代数结构，提出了一个针对S盒的代数结构的新的评估方法。

为解决上述问题，本发明密码S盒评估新方法，包括全排列产生模块、随机数产生模块、局部线性检测模块、局部二次检测模块，评估方法包括以下步骤：

S1：利用全排列产生模块产生一组数的全排列，该模块输出为一个4维或8维的数组，将其定义为排列C；

S2：利用随机数产生模块产生3组，每组60个随机数，并且这三组随机数在相同的位置的值是不能相同的，该模块的输出为三个60维的数组，将其定义为A1，A2，A3；

S3：将数组A1，A2和排列C输入到局部线性检测模块；

局部线性检测模块按照某一个顺序对S盒的输入进行固定后，可以得到的线性表达式的个数，该模块的输入为A1，A2，C，输出为两个数组C1，C2，其中，C1中存储的为此时固定的顺序，C2中存储的为对应的线性关系的个数；

S4：将数组A1，A2，A3和排列C输入到局部二次检测模块；

局部二次检测模块按照某一个顺序对S盒的输入进行固定后，可以得到的最高代数次数为二次的表达式的个数，该模块的输入为A1，A2，A3，C，输出为两个数组C，D2，其中，C中存储的为此时固定的顺序，D2中存储的为对应的二次关系的个数；

S5：根据局部线性检测模块的输出和局部二次检测模块的输出对S盒进行评估，如果对于局部线性检测模块的输出C2中存储的数的和与2^n-1相差较少，说明S盒的代数结构较好；如果局部线性检测模块的输出C2中存储的数的和与2^n-1相差较大，说明S盒的代数结构较差；对于局部二次检测模块的输出D2，如果D2[i]的值较大，而i的值较小，如i＝4或5，说明S盒的代数结构较差；如果D2[i]的值较大，但是i的值也较大，如i＝6，说明S盒的代数结构较好。

与现有的密码S盒的评估方法相比，本发明公开了一种密码S盒评估新方法，对密码S盒的代数结构进行了评估。这种新的评估方法如果应用到密码算法S盒的设计中，将会避免S盒在代数结构上的缺陷，对设计安全性较高的S盒具有很重要的意义。

附图说明

图1为实施例密码S盒评估方法的流程框图。

图2为实施例中S3.1步骤的说明图。

图3为实施例中S3.2步骤的说明图。

图4为实施例中S3.3步骤的说明图。

图5为实施例中S3.4步骤的说明图。

具体实施方式

下面结合附图和实施例对本发明内容作进一步的说明，但不是对本发明的限定。

实施例

参照图1，密码S盒评估方法的流程框图，以8位的密码S盒为例，评估方法包括如下的步骤：

S1：利用全排列产生模块产生一个[1,2,3,4,5,6,7,8]的排列C。

S2：利用随机数产生模块产生三个不同的数组A1，A2，A3。

S3：将数组A1，A2和排列C输入到局部线性检测模块；

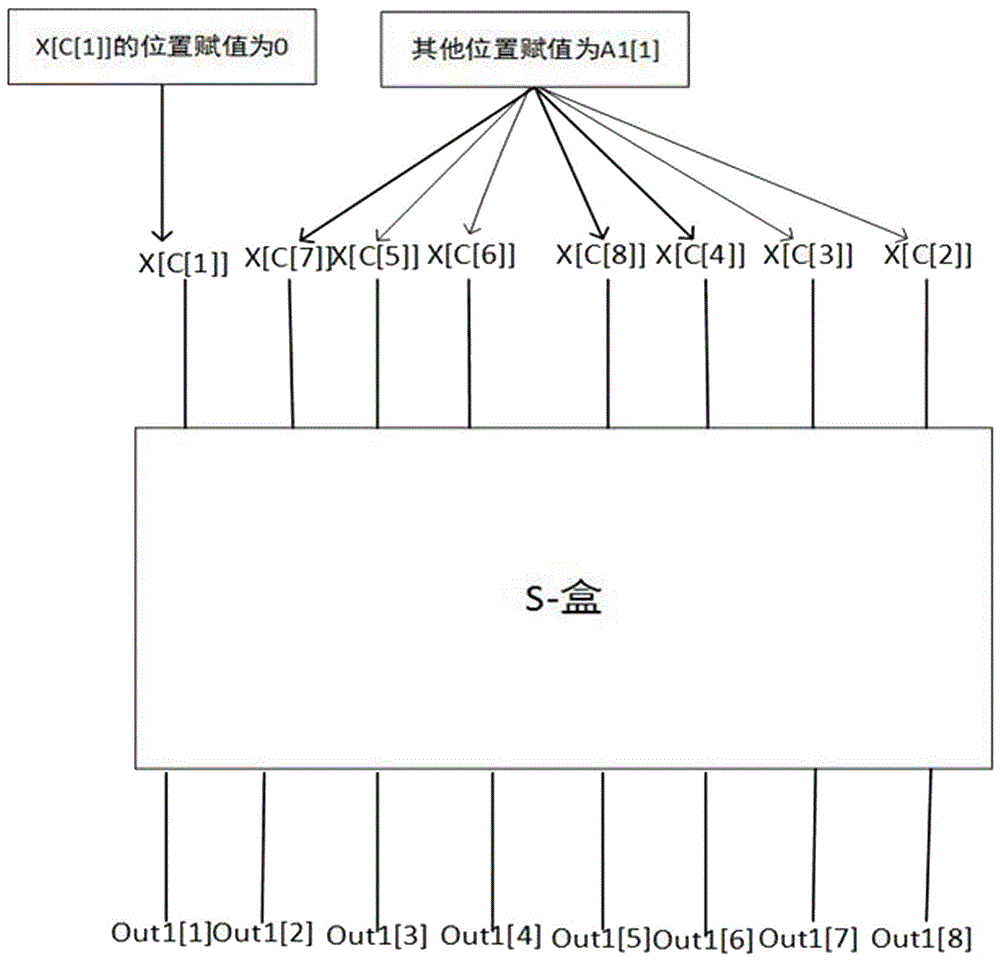
S3.1：在这个模块中，首先，对于密码S盒的输入X，先固定X[C[1]]为0，将X[C[2]]，X[C[3]]，X[C[4]]，X[C[5]]，X[C[6]]，X[C[7]]，X[C[8]]赋值为A1[1]中对应的十进制数的二进制形式，得到了一个密码S盒的输出Out1，参照图2；

S3.2：再将X[C[2]]，X[C[3]]，X[C[4]]，X[C[5]]，X[C[6]]，X[C[7]]，X[C[8]]，赋值为A2[1]中对应的十进制数的二进制形式，得到了另一个密码S盒的输出Out2，参照图3；

S3.3：将X[C[2]]，X[C[3]]，X[C[4]]，X[C[5]]，X[C[6]]，X[C[7]]，X[C[8]]赋值为A1[1]与A2[1]的二进制异或后的值，得到的密码S盒的输出为Out3，参照图4；

S3.4：最后，将X[C[2]]，X[C[3]]，X[C[4]]，X[C[5]]，X[C[6]]，X[C[7]]，X[C[8]]赋值为全零，得到密码S盒的一个输出Out4，参照图5，并利用公式

f(x₁+x₂)＝f(x₁)+f(x₂)+f(0)

判断密码S盒的每一位的输出是否都是满足上面的关系，即

Out3[i]＝Out1[i]+Out2[i]+Out4[i](1<＝i<＝8)

S3.5：按照S3.1，S3.2，S3.3，S3.4，再将A1[2]-A1[60]以及A2[2]-A2[60]分别带入到X[C[2]]，X[C[3]]，X[C[4]]，X[C[5]]，X[C[6]]，X[C[7]]，X[C[8]]，如果输出都是满足上面的关系，将C2[1]加1；

S3.6：之后再固定X[C[1]]为1，并按照S3.1，S3.2，S3.3，S3.4，S3.5，判断此时得到的表达式是否满足线性关系，如果是满足的，将C2[1]加1；

S3.7：扩大固定的位数i，按照S3.1，S3.2，S3.3，S3.4，S3.5，S3.6，判断此时得到的表达式是否是满足线性关系，如果是满足的，将C2[i]加1；

S3.8：当固定的位数i从1-7跑完后，得到了一个数组C2后，用C2[i]＝C2[i]-2C2[i-1]计算C2，如果C[i](i<7)至少有一个不为0，将C，C2输出，此时得到的C2[i]的值才是固定i位后，得到的线性关系的个数；得到的C2[i]为按照C的顺序固定i位后得到的线性关系的个数。

对于S3的伪代码如下：

函数Linear(i,num,C,A1[k],Out1)表示按照C中的顺序，固定i位，并将固定的位置赋值为num的二进制的形式，非固定的位置赋值为A1[k]的二进制的形式，得到的输出为Out1。

S4：如果，C2[i]＝0(i<7)，则表示没有通过局部线性检测，此时，将数组A1，A2，A3和排列C输入到局部二次检测模块；

S4.1：在这个模块中，首先，对于密码S盒的输入X，先固定X[C[1]]为0，将X[C[2]]，X[C[3]]，X[C[4]]，X[C[5]]，X[C[6]]，X[C[7]]，X[C[8]]分别赋值为A1[1]，A2[1]，A3[1]中对应的十进制数的二进制形式，得到了一个密码S盒的输出分别为Out1，Out2，Out3；

S4.2：将X[C[2]]，X[C[3]]，X[C[4]]，X[C[5]]，X[C[6]]，X[C[7]]，X[C[8]]赋值为全零，得到密码S盒的一个输出Out4；

S4.3：最后，将A1[1]^A2[1]、A1[1]^A3[1]、A2[1]^A3[1]、A1[1]^A2[1]^A3[1]对应的二进制的形式分别赋值到X[C[2]]，X[C[3]]，X[C[4]]，X[C[5]]，X[C[6]]，X[C[7]]，X[C[8]]，得到对应的密码S盒的输出分别为Out5，Out6，Out7，Out8；并利用公式

f(x₁+x₂+x₃)＝f(x₁+x₂)+f(x₁+x₃)+f(x₂+x₃)+f(x₁)+f(x₂)+f(x₃)+f(0)Out8[i]＝Out1[i]+Out2[i]+Out3[i]+Out4[i]+Out5[i]+Out6[i]+Out7[i](1<＝i<＝8)判断密码S盒的每一位的输出是否都是满足上面的关系，

S4.4：按照S4.1，S4.2，S4.3，再将A1[2]-A1[60]以及A2[2]-A2[60]分别带入到X[C[2]]，X[C[3]]，X[C[4]]，X[C[5]]，X[C[6]]，X[C[7]]，X[C[8]]，如果输出都是满足上面的关系，将D2[1]加1；

S4.5：之后再固定X[C[1]]为1，并按照S4.1，S4.2，S4.3，S4.4，判断此时得到的表达式是否满足二次关系，如果是满足的，将D2[1]加1；

S4.6：扩大固定的位数i，并按照S4.1，S4.2，S4.3，S4.4，S4.5，判断此时得到的表达式是否是满足二次关系，如果是满足的，将D2[i]加1；

S4.7：最后，当固定的位数i从1-7跑完后，得到了一个数组D2，如果D2[i](i<6)至少有一个不为零，将C，D2输出，得到的D2[i]为按照C的顺序固定i位后得到的二次关系的个数。

对于S4的伪代码的形式如下：

S5：根据局部线性检测模块和局部二次检测模块的输出，对S盒进行评估。如果对于局部线性检测模块的输出C2中存储的数的和与2^n-1相差较少，说明S盒的代数结构性质较好；如果局部线性检测模块的输出C2中存储的数的和与2^n-1相差较大，说明S盒的代数结构较差；对于局部二次检测模块的输出D2，如果D2[i]的值较大，而i的值较小，如i＝4或5，说明S盒的代数结构较差；如果D2[i]的值较大，但是i的值也较大，如i＝6，说明S盒的代数结构较好。

在随机数产生模块中，使用了C语言中自带的函数rand()模2^n-i，产生了数组A1，数组A2为在数组A1的基础上，A2[i]＝(A1[i]+11)mod(2^n-i)，数组A3为在A1，A2的基础上，A3[i]＝(A1[i]+A2[i])mod(2^n-i)。这样做可以使每一个数组对应的位置的值是不同的，并且能够达到随机的效果。

对于S3，如果在C2[4]，C2[5]，C2[6]的位置至少有一个不为零，则此时不用再执行S4，这样可以很好的提高程序运行的速度。

本发明提出的S盒评估新方法，对于今后设计性质更好的S盒也具有很大的参考价值。

下面通过对一些算法的测试，对本发明进行进一步详细的说明：

利用本发明的评估方法，对AES，SMS4，以及ZUC算法的S盒的代数结构进行评估，具体步骤如下：

步骤一：将AES，SMS4，和ZUC算法的S盒放到评估方法中；

步骤二：按照评估方法中S1和S2，分别产生一个固定的顺序C和三个随机数组A1，A2，A3；

步骤三：按照评估方法中S3，对AES，SMS4以及FOX算法的S盒进行测试，如果对于固定的位数i<7时，存在线性关系，则将对应的固定的顺序C以及得到的线性关系的个数C2打印出来；

步骤四：如果对于某一个固定顺序，i<7时不存在线性关系，则利用评估方法中的S4进行二次检测；如果存在二次关系，则将固定的顺序以及得到的二次关系的个数打印出来。

步骤五：利用评估方法中的S5对得到的数据进行分析。测试得到的结果为表1-1。

表1-1

通过测试，可以发现AES的S盒以及AES的S逆盒的为128，SMS4的S盒的为127，这些算法的值与128相差不大，说明其S盒的设计具有很好的代数结构。而FOX算法的为121与128相差较大，说明其代数结构较差，可以利用它的这种性质构造区分器，对其进行分析。