模乘设备和方法与流程

背景技术：

本发明通常涉及数据处理，更具体地涉及一种模乘方法和设备。

模乘被用于许多领域中，特别是数据安全系统，例如密码系统。密码系统使用取决于长整数乘数之间的模乘的密码方案。整个密码系统的性能密切地依赖于模乘的最优化。

密码系统被广泛用于许多产品中，例如嵌入式设备、智能卡，以确保经由非安全信道传送的消息的隐私性和真实性。非对称密码系统(也称作“公开密钥”密码系统)使用包括公开密钥和私有密钥的一对密钥来加密和解密消息，以便确保该消息安全到达而没有被未授权的用户拦截。

非对称密码系统可能遭受意图是获取私有密钥的不同类型的攻击。第一种类型的攻击是基于对私有密钥的搜索。这种攻击的计算复杂性依赖于私有密钥中包括的比特的数量。因此，可以通过选择由大量比特组成的私有密钥来保护非对称密码系统免受该类型的攻击。然而，其它类型的攻击的目标是带有由大量比特构成的密钥的密码系统。这些攻击使用数学最优化或解析最优化以设法降低搜索空间。

还存在基于对密码设备的行为的分析对鲁棒的密码系统实施的间接攻击，密码设备被看作含有已知算法和未知密钥的黑盒子。这种间接攻击包括“边信道攻击”或sca，其使用在密码算法的执行期间观察到的信息(“边信道信息”，例如密码设备的功耗)以检索嵌入密码设备中的一些秘密信息(paulkocher.timingattacksonimplementationsofdiffie-hellman，rsa，dss，andothersystems.n.koblitz编辑，advancesincryptology-crypto’96，lecturenotesincomputerscience，第1109卷，第104-113页.springer-verlag，1996)。

被证实非常有效的特定类型的边信道攻击通过将故意的(蓄意的)故障注入至密码设备中并观察对应的错误输出(差分故障分析(dfa))来实现。这种攻击限制了为得到秘密密钥的比特所必需的实验的次数。

已经涌现了各种各样的对抗措施系统和方法以保护非对称密码系统免受这种间接攻击。间接攻击可以针对许多密码系统，例如rsa密码系统、公开密钥密码系统、或者椭圆曲线密码系统。具体而言，诸如移动设备或智能卡等基于椭圆曲线密码的嵌入式设备对边信道攻击(sca)是特别敏感的。现在椭圆曲线密码系统(ecc)被看作是rsa密码系统的强有力且大众化的替代物，因为它们需要比rsa更短的密钥长度且提高了安全水平。

在很多情况下，通过使用多倍长度奇整数作为模数的算术运算来实施公开密钥加密。该算术运算的速度影响系统的性能。特别适合于密码系统的一种模乘方法是蒙哥马利模乘。蒙哥马利模乘(在下文中称为mmm)存在于允许在有限域或环中计算算术运算的运算中。它具有快速实施，这使得当需要许多乘法时，像在大多数密码非对称算法中，它相对于简单模乘是优选的。例如，rsa(李维斯特、萨莫尔、阿德曼)经由乘法环计算模幂运算，于是模幂运算形成一系列乘法。幂数通常很大，典型地是2048比特或更大，因此每rsa几千个乘法。

使用模乘的另一个众所周知的密码方案是椭圆曲线密码术(ecc)，其存在于对有限jfq的运算，其中q是素数的幂。对于该曲线上的每一运算(两倍或加法，由于曲线是组)，几个(典型的大约十个)乘法是必需的。进一步，在该曲线上运算的数量是几百个，因此每一个ecc计算总共几千个乘法。

′lln中两个元素x和y的乘积的简单实现是像x和y是整数一样地计算xy，然后将该结果约简(reduce)模n。一个可能是对xy减去n，直到该结果严格小于n。然而，该算法非常低效。更快的替代算法是用xy除以n，并且仅保留余数。但是这种欧几里德除法代价非常高(比乘积多5到20)。mmm允许避免除法的模乘的快速计算。它被调整以适应计算机的架构。定义基数r为2w的大于模数n的最小次幂，例如，当n取2048比特时，则如果w＝32比特，n＝(2^w)⁶⁴＝2^64w＝2²⁰⁴⁸。

mmm需要投入参数至所谓的蒙哥马利表示法。mmm在该表示法内计算实际的模乘并且有效率地完成，因为乘法和约简可以交叉，从而保持小尺寸的中间乘积。利用mmm，以2的幂为模替代最初的模来执行约简(交叉或不交叉)。以2的幂为模的约简包括比特的位移，而非执行真正的除法。

mmm依赖于被称为基数r的一个系数。出于效率原因，r通常选择为2的较大次幂。依赖于r的相对值和模数n，mmm可能需要额外的约简步骤。

典型地，对于密码大小的模数，例如rsa的1024、2048、4096比特，或者ecc的196、256、512，出于性能原因，基数r的值被选择为(严格)大于该模数的2的最小次幂。

有限环或域中的数在机器中被表示为一系列被称为分支(limb)的数字，且其对应于机器自然比特宽度(例如8、16、32或64比特)。此外，模数大小都是分支比特宽度的倍数。相应地，如果基数r被选择为最小值的两倍(r为2的幂)，则所有的计算一定是基于具有额外分支的整数而执行的。这样导致更多的运算被执行。

利用r的该选择，mmm算法结束于最终测试(也被称为“额外约简”)：它返回正确的结果或正确的结果加上模数，并且因此应该被约简。如果r不是大于模数的2的最小次幂，而是大于模数的2的第二小、第三小次幂等，则不存在这种“额外约简”。

然而，该额外约简的存在有一些显著缺点：

-第一，额外约简引发计算时间的平均增长(尽管如此，与计算中的额外分支的添加相比是可忽略不计的)；

-第二并且最重要的，该额外约简导致引起重大安全问题的数据泄漏。

额外约简的存在或缺失依赖于mmm的输入。因此，在该情况下，用户是企图恢复私有密钥的潜在的攻击者。例如，如果攻击者能够通过猜测私有密钥的一些比特来预测算法的内部值，然后使用的实际值可以通过观察对额外约简的效果而被确定。始终匹配(基于若干加密)额外约简的存在或缺失的内部值是最可能的。

对额外约简的观察可以通过若干方式实现，例如通过监测计算的总持续时间。如果有额外约简，那么该总持续时间较长。尽管如此，总持续时间仅产生额外约简存在的大致想法，因为总持续时间实际上受若干(可能几千)额外约简的影响。因此，通常执行对额外约简存在的直接观察。它可能需要对机器的物理访问以及使用磁探头(或者用于侦查瞬间电流消耗的装置)。因此额外约简辐射或消耗分布可以被表征，并且稍后在新的迹线通过“模式匹配”来识别。

经常，通过在计算之前使处理的数据随机化，以及在计算之后且恰在输出结果之前使数据解除随机化，使非对称算法的实施被堵塞(blind)。这种对抗措施阻止攻击者猜测内部值，并且结果基于对内部值的预测的先前攻击不现实。

然而，据观察，乘法的序列仍可被猜测，尽管它们操纵未知的数据。

例如，考虑密码算法的实施，其中如果一个密钥比特等于1，则一个mmm的输出馈送另一mmm(其恰巧是平方，两个输入都相等的mmm)，或者否则不馈送平方。据分析，如果该密钥比特等于1，即一个mmm作为平方馈送另一个)，则如果第一个mmm具有额外约简，那么很有可能第二个mmm不具有额外约简，反之亦然。于是正如所示，在两个连续的mmm上的额外约简的存在之间存在负相关性。相应地，如果两个mmm不接连发生(即，它们处理独立的数据)，则额外约简的存在被解除相关。

因此，甚至在存在对抗措施(数据堵塞，并且甚至规则的指数方案)的情况下，额外约简的存在能够允许攻击者提取密钥。

相应地，需要有一种改进的方法和设备以保护非对称密码系统免受基于对额外约简的观察的攻击。

技术实现要素：

为了解决这些和其它问题，提供了用于以给定模数为模执行第一被乘数和第二被乘数的乘法的模乘设备，被乘数中的每一个包括给定数量的数字，每一个数字具有给定字长。模乘设备包括：

-用于使第一被乘数中的至少一个数字与第二被乘数相乘以产生乘法器输出的乘法器；

-模约简单元，其被配置为通过扩展模数和整数系数的乘积来约简从乘法器输出得到的量，扩展模数是给定模数与扩展参数的乘积，模约简单元提供约简输出，约简输出是严格小于扩展模数的正整数，其中模乘设备进一步包括选择单元，选择单元被配置为选择扩展参数以使设备执行乘法所耗费的时间独立于被乘数。

在一个实施例中，该设备可以被分配存储器空间以存储字，存储器空间的最大尺寸由整数常数定义，并且选择单元被配置为将扩展参数选择为整数常数与模数的两倍之间的比值的函数。

在某些实施例中，选择单元可以被配置为将扩展参数选择为低于比值。

在一个实施例中，选择单元可以被配置为在严格包括在1与该比值之间的区间内选择扩展参数。

整数常数可以是2的指数次幂，指数等于字长与整数加1的乘积，整数表示用于表示模数的字的数量。

特别地，选择单元被配置为在严格包括在1和上阈值之间的区间内选择扩展参数，上阈值被定义为2的字长次幂除以2。

扩展参数是小于2的字长次幂的一半的最大素数。

在某些实施例中，乘法器可以被配置为使包括至少一个数字的第一被乘数中的一组数字与第二被乘数迭代相乘，这提供了中间乘法器输出，并且模约简单元迭代约简每一个中间乘法器输出，这提供了中间约简输出，模乘设备进一步包括至少一个加法器以将中间约简输出相加。

选择单元可以被配置为通过迭代更新扩展参数。

替代地，选择单元可以被配置为通过迭代选择相同的扩展参数。

在另一实施例中，乘法器可以被配置为使第一被乘数与第二被乘数相乘，其提供主乘法器输出，并且模约简单元被配置为约简主乘法器输出。

进一步提供了蒙哥马利乘法引擎，其包括根据前述实施例中的任何一个实施例的模乘设备，该模乘设备包括：

-系数确定单元，被配置为根据从乘法器输出得到的值和整数常数确定整数系数，整数常数高于模数且是2的字长次幂，其提供了整数系数；

-除法单元，被配置为将约简输出除以整数常数。

整数常数则是正数。

进一步提供了巴雷特乘法引擎，其包括根据前述的实施例中的任何一个实施例的模乘设备，整数系数为负数。

还提供了克里斯托弗乘法引擎，其包括根据前述的实施例中的任何一个实施例的模乘设备，整数系数是负数。

另外，本发明提供了用于在电子设备中实施密码算法的密码系统，密码算法基于两个被乘数之间的至少一个模乘的结果，其中密码系统包括根据前述实施例中的任何一个实施例的模乘设备以执行至少一个模乘。

密码算法可以是李维斯特、萨莫尔、和阿德曼(rsa)算法，密码算法包括模指数运算单元以计算消息的指数，rsa密码算法基于私有密钥d、公开密钥e和系统系数p、q，其中p和q是素数以使公开密钥e是(p-1)和(q-1)的素数，密码系统包括指数运算单元，其用于以等于pq的模数为模对消息的e次幂进行指数运算，该指数运算单元使用模乘设备迭代执行对消息的指数运算。

密码算法可以是取决于给定椭圆曲线的椭圆曲线密码算法，该系统包括标量乘法单元，其被配置为接收在有限域上的坐标系中定义的椭圆曲线的点的两个坐标、以及为二进制数的密钥，以生成二进制数与椭圆曲线的点之间的标量乘法的结果，标量乘法单元包括模乘设备。

进一步提供了用于以给定模数为模执行第一被乘数和第二被乘数的乘法的方法，所述被乘数中的每一个包括给定数量的数字，每一个数字具有给定字长，该方法包括：

-将第一被乘数中的至少一个数字与所述第二被乘数相乘以产生乘法器输出；

-通过扩展模数和整数系数的乘积来约简从所述乘法器输出得到的量，所述扩展模数是所述给定模数与扩展参数的乘积，其提供约简输出，所述约简输出是严格小于所述扩展模数的正整数，

所述方法进一步包括选择所述扩展参数以使所述设备执行所述乘法所耗费的时间独立于所述被乘数。

附图说明

被并入并构成本说明书的一部分的附图例示了本发明的各种实施例，并且连同如上给出的本发明的一般描述和如下给出的实施例的详细描述一起用来解释本发明的实施例。

图1表示根据本发明的某些实施例的密码系统。

图2是根据某些实施例的表示模乘设备的框图。

图3是根据某些实施例的描绘模乘方法的流程图。

图4是描绘在蒙哥马利引擎中实施的乘法方法的实施例的流程图。

图5根据本发明的一种应用的描绘包括指数运算单元的密码系统。

图6是根据某些实施例的描绘模指数运算方法的流程图。

图7是根据某些实施例的描绘椭圆曲线标量乘法方法的流程图。

注意，本发明的附图不一定按比例绘制。附图仅仅是示意性表示。附图旨在仅描绘本发明的典型实施例，并且因此不应被认为限制本发明的范围。

具体实施方式

本发明的实施例提供了改进的模乘方法和设备以确定两个被乘数的模乘的结果，每个被乘数中包括多个数字。

本发明的实施例进一步提供了密码系统和方法，其在密码运算中使用这种模乘方法和设备的结果以确保保护密码系统和方法免受常规上基于对额外约简的观察的攻击。示例性密码运算包括加密、解密运算、签名和认证运算。仅出于例示的目的，将参考例如加密和/或解密运算来做出对某些实施例的以下描述。

参考图1，表示了根据本发明的某些实施例的密码系统100。密码系统100包括模乘设备10，其配置为以给定模数n为模执行第一被乘数x和第二被乘数y的模乘。每个被乘数x和y包括给定数量的数字，每个数字具有给定字长w(例如w＝8、32或64比特)。

模乘设备10可以在硬件或软件模块中实施并对一组参数进行运算以根据两个输入x和y产生被标记为的模乘结果。

为初始化模乘设备10，该设备可以加载模数n和乘法常数rext。

密码系统100可以包括执行指令的处理器。处理器可以是基于寄存器的处理器，包括寄存器以存储要约简的值的分量，例如模数n和乘法常数rext。

存储器14可以用于存储由模乘设备10执行的运算的结果。

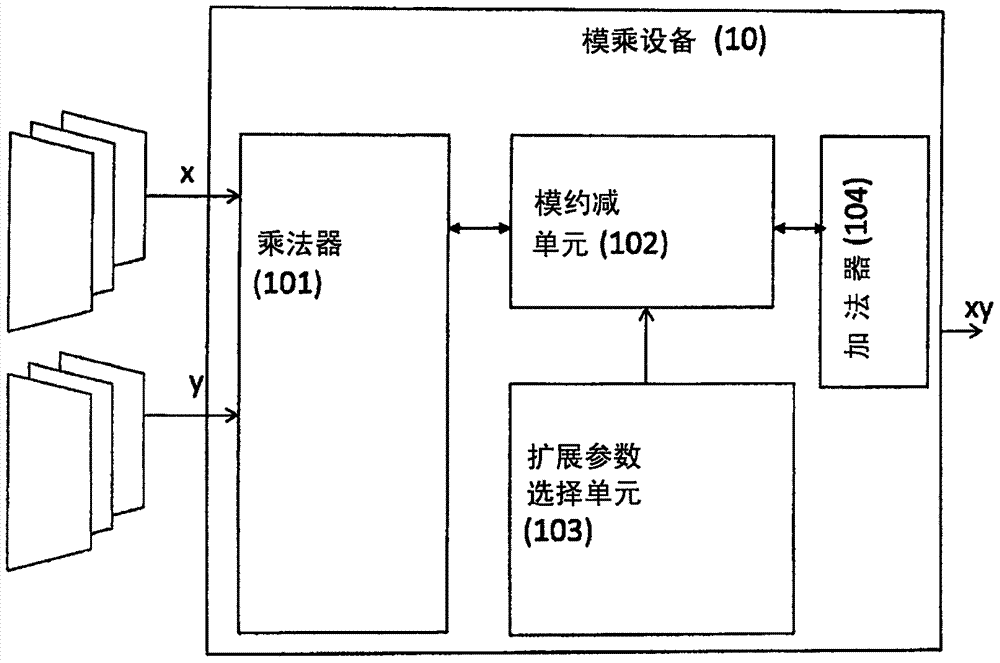
图2是根据某些实施例的表示模乘设备的框图。

模乘设备10包括用于将第一被乘数中的至少一个数字与所述第二被乘数相乘以产生乘法器输出的乘法器101。

模乘设备10进一步包括模约简单元102，其被配置为以给定扩展模数nr为模约简乘法器输出，扩展模数被定义为所述给定模数n与扩展参数r的乘积，模约简单元102提供约简输出，约简输出是严格小于扩展模数nr的正整数。

根据本发明的一个方面，模乘设备10进一步包括选择单元103，其被被配置为选择扩展参数r以使所述设备执行所述乘法耗费的时间独立于所述被乘数。因此模乘在确定的时间内完成并允许通过以r为模对计算进行约简的非琐碎计算检查。相应地，模乘在常数时间内执行，而无需有条件的约简，因此保护密码系统100免受基于这种常规约简的攻击并确保故障注入抵抗，同时在计算方面几乎不具有开销。

模乘设备10可以被分配存储器空间以在存储器14中存储字，所述存储器空间的最大尺寸由整数常数rext(在下文中也被称作“乘法常数”)定义。因此乘法常数rext表示被分配给模乘的字的最大数量。存储器空间可以用于存储用于执行模乘运算的数据，例如输入(被乘数)、输出(模乘结果)和用于执行模乘运算的中间值。

在某些实施例中，选择单元103可以被配置为将扩展参数r选择为参数的函数，该参数被定义为所述乘法常数rext与所述模数的两倍2n之间的比值。

特别地，选择单元103可以被配置为将扩展参数r选择为使扩展参数严格低于参数

这允许在确定时间内进行模乘设备的运算(即没有额外约简)。

在一个实施例中，选择单元103可以被配置为具体在严格包括在1和比值之间的区间内选择扩展参数。

在优选实施例中，乘法常数rext可以高于n和2的指数次幂，该指数等于所述字长w与整数l加1的乘积，整数l表示用于表示模数n的字的数量：

rext＝2^w(l+1)

扩展参数r可以相应地在区间内选择。

通过在范围i中选择扩展参数r，可以消除对额外约简的需要，由此阻止攻击者甚至在存在对抗措施时提取秘密密钥。

特别地，选择单元103可以被配置为在严格包括在1和上阈值之间的区间j中选择所述扩展参数，上阈值被定义为2的字长次幂2^w与2之间的比值：

仅出于例示的目的，本发明的某些实施例的下列描述将主要参考等于2^w(l+1)的乘法常数rext和在区间i中选择的扩展参数。

扩展参数r可以是素数以进一步增加故障检测的能力。在某些实施例中，乘法器可以被配置为将包括至少一个数字的第一被乘数x中的一组数字与第二被乘数y迭代相乘，这提供了中间乘法器输出，并且所述模约简单元101可以被配置为迭代地约简每一个中间乘法器输出，这提供了中间约简输出。模乘设备10可以进一步包括至少一个加法器104以将中间约简输出相加。

替代地，乘法器101可以将第一被乘数x与第二被乘数y相乘，这提供了主乘法器输出，然后模约简单元102约简主乘法器输出。

密码系统100可以例如是非对称密码系统，其由使用多倍长度整数作为模数n的算数运算实施公开密钥加密。例如，在rsa密码系统中，由在余数计算系统中使用奇合数作为模数的幂计算来执行加密和解密。在素数域fp上的椭圆曲线加密中，在椭圆曲线上的点的加法通过使用奇素数作为模数的加法、减法、乘法和除法的恰当组合来实施，并且通过重复点加法运算量执行加密和解密。

在一个实施例中，模乘设备10可以在蒙哥马利乘法引擎中实施。

在蒙哥马利乘法引擎(也被称为蒙哥马利约简引擎)中，关于模数n的计算是基于使用被称为蒙哥马利基数或蒙哥马利底数的辅助数r，以使gcd(r，n)＝1。

在某些实施例中，模数n可以是素数，然后基数优选地被设置为2的某一指数l，典型地被选择为大于模数的2的第一实用幂(r＝2^l)。

两个数a和b的蒙哥马利乘法是它们的乘积的蒙哥马利约简，被写作

当r和n满足gcd(r，n)＝1时，存在两个数r^-1和n’符合0＜r^-1＜n且0＜n’＜r，满足rr^-1-nn’＝1。

本发明的实施例提供通过注入扩展参数r的选定值的改进的蒙哥马利模乘引擎。

根据本发明的实施例的密码系统和方法可以应用于对不同的公开密钥加密技术(例如基于rsa或ecsm(椭圆曲线标量乘法)的系统)的指数运算执行带有或不带有最终约简的蒙哥马利乘法。

数c与基数r的蒙哥马利约简和素数模数n表示由cr^-1modn给出的量。

两个数a和b的蒙哥马利乘法表示它们的乘积的蒙哥马利约简，被写为

如本文使用的，符号x横表示蒙哥马利乘法运算。

模乘设备10可以在蒙哥马利引擎中实施以计算两个被乘数x和y的蒙哥马利乘积

蒙哥马利引擎10可以在硬件或软件模块中实施并对一组参数进行运算以产生结果。例如，引擎可以用于对两个输入x和y产生结果

蒙哥马利引擎10也可以被配置为转换成蒙哥马利形式，或者从蒙哥马利形式转换。为转化成蒙哥马利形式，引擎接收a和r²作为输入，并产生输出相反地，为了转化回到常规形式，引擎接收和1作为输入，并输出

蒙哥马利引擎也可以被配置为计算数的蒙哥马利约简。在该情况下，引擎接收a和1作为输入，并产生作为输出。

在蒙哥马利引擎中，以数的蒙哥马利形式对数进行计算(数x的蒙哥马利形式被定义为)。

在一些密码方案中，给定模数n，对以素数为模的数进行运算，基数r可以被表达为基数2的形式，例如2的某一正整数指数wl(r＝2^wl)，其中w是机器的比特字长，并且l表示需要表示模数n的字的数量。

参考图3，根据本发明的某些实施例呈现了描绘模乘方法的流程图。

在步骤200中，加载正整数模数整数n和乘法常数rext，并接收被乘数x和y。

乘法常数rext可以以2为底数被定义为数2的w(l+1)指数，其中l表示用于表示模数n的字的数量，并且w指定字长：

rext＝2^w(l+1)

在步骤202中，在范围中选择扩展参数r。

在步骤204中，第一被乘数x的至少一个数字x1与第二被乘数y相乘。

在步骤206中，确定量a＝x1y±unr，其中u被确定为使u≤rext(x1y以nr为模被约简)。

取决于本发明的应用，方法可以包括使用乘法常数rext对约简结果a施加运算，这提供了量a’。

可以例如通过估计x1*y(或者在蒙哥马利引擎的情况下x1*y*r^-1)除以nr的商来确定参数u，这种估计是使得q-2≤u≤q，其中q表示精确的商。

在步骤208中，可以返回量a或从a得到的量a’。

扩展参数r避免了对以nr为模进行进一步约简以使结果适应寄存器大小的需求。具体而言，在区间中选择素数类型的扩展参数r允许阻止基于差分功率分析和相关功率分析的攻击。具体而言，在某些实施例中，在步骤202中，可以选择r以使：

其中l表示正整数。

常规方法应用模数扩展nr的默认选择以进行故障检测，其在w的比特宽度倍数上保持nr，由此造成关于边信道攻击的弱点，因为如果r固定在两个字，则需要利用r＝2^w(l+1)进行额外的约简。相反，根据本发明的实施例的r的选择允许在消除额外约简的同时检测故障。

取决于本发明的应用(例如某些指数应用)，可以具体在范围中的区间内选择扩展参数。

在某些实施例中，可以选择l等于用于表示模数n的字的数量，并且可以在区间内选择r。相应地，计算可以仅扩展一个字。

扩展参数r可以被随机选择或在区间内根据某些标准进行选择以阻止基于差分功率分析和相关功率分析的攻击(例如，以使nr的不同值之间的汉明距离大。)

具体而言，r可以被设置为2(r＝2)以使模数扩展nr尽可能的小。作为结果，大量的最高有效比特可以被设置为0。因此电路可以操作多个零值比特，从而减小功率消耗。

在某些实施例中，乘法步骤204可以被迭代执行以将第一被乘数x中的一组数字与第二被乘数y相乘，这提供了中间乘法器输出，并且约简步骤可以被迭代以约简每一个中间乘法器输出，这提供了中间约简输出，模乘方法进一步包括中间约简输出。

扩展参数r可以被设置用于步骤204至210的所有迭代或步骤204至210的一组迭代或每一个迭代的验算。

乘法步骤204可以替代地将第一被乘数与所述第二被乘数直接相乘并将约简步骤206应用于由此获得的乘法结果。

图4是描绘在蒙哥马利引擎中实施的乘法方法的实施例的流程图。

在步骤300中，接收正整数模数整数n并接收常数rext。

在步骤302中，选择扩展参数，如关于步骤202描述的那样选择基数r。

在步骤303中，可以在[0，rext-1]中选择整数n’，以使：

nrn′≡-1(modrext)

在步骤304中，执行乘法步骤。其包括确定量＝xyn′modrext。

在步骤306中，确定量a＝(xy+unr)(通过以nr为模约简xy确定a)。

在步骤307中，将量a除以rext，提供了从a′得到的量a′。

在步骤308中，由蒙哥马利引擎返回量a′(例如发布至请求应用)。

应注意，取模和除以rext的运算可以在于忽略用于模运算的一些比特以及针对除法运算进行移位。如果rext是2的幂，则这在某些实施例中排除了对明确存储乘法常数rext的需求。

没有最终约简的蒙哥马利乘法函数在下文中被记为

在某些实施例中，模乘方法可以用于执行指数运算。

图5描绘根据指数应用的包括指数单元的密码系统100。

密码系统100使用模乘设备10来计算整数a(被称作底数)的模指数运算。给定底数a的模指数运算表示当底数a为d次(被称作指数)幂a^d并被除以模数n时的余数。模指数运算方法可以用于公开密钥密码系统100中以确定很多乘积。

根据某些实施例，可以使用以下函数来计算模指数运算：c≡a^d(modn)。存在若干指数运算方法以计算乘法运算(基本乘法运算)的n次迭代而非d次迭代，例如《左到右二进制方法》或《右到左二进制方法》。因此模指数运算方法可以包含对模乘方法的若干次调用。

为计算基本乘法运算，模指数运算方法可以使用由模乘设备10(例如蒙哥马利引擎)实施的模乘方法，因为它具有低的计算复杂度。仅出于例示的目的，下面将参考模乘方法到蒙哥马利引擎的应用来描述指数运算方法某些实施例。

图6是根据某些实施例的描绘模指数运算方法的流程图。

在步骤500中，接收正整数模数整数n和乘法常数rext。

在步骤502中，根据关于图3的步骤202描述的那样选择扩展参数r。

在步骤504中，计算量

在步骤506中，使用指数函数从递归计算模指数运算以确定

这包括调用若干次模乘函数以计算基本乘法运算。通过实施图2的步骤204至208，每次迭代确定每一次随后的乘法调用模乘函数的步骤204至208以递归地计算的当前值和的乘积。

(d-1)次迭代蒙哥马利乘法函数提供的d次幂：

在步骤508中，可以执行后置处理步骤以使用没有约简的模乘方法从确定(标记为)：

在步骤510中，返回底数a的d次幂为：

应注意，选择步骤502可以被执行一次或在模乘方法的每一次迭代中被执行(在该情况下，步骤202被迭代并且步骤502被去除)。

为排除对额外约简的需求，可以选择大于极小值r的rext，即，rext＝2^w(l+1)并且可以选择r为素数以使nr具有小于rext的至少一个比特，以去除对额外约简条件的需求。这导致执行从n至nr的模数扩展，其中r是满足如下等式的素数：

在其它实施例中，模乘函数可以用于在椭圆曲线密码系统100中执行ecsm(椭圆曲线标量乘法)。

事实上，故障攻击不仅针对rsa密码系统而且针对椭圆曲线密码系统。椭圆曲线上的运算可以用于非对称密码系统100中。

椭圆曲线通常被定义为在一些域中满足被称为魏尔斯特拉斯方程的某些三次方程的一组点，即被定义为魏尔斯特拉斯方程的曲线。数学上，它们代表平面曲线的特殊类。能够以各种表达式表示椭圆曲线和它们的点，例如仿射坐标、投影坐标、雅克比坐标和蒙哥马利形式。

用于密码学中的椭圆曲线被定义在具有p素数的素数域上或者在一些大的的二进制域上。它们特别适合具有存储器约束的嵌入式设备的实施。由于这些设备的物理特征和它们在潜在的敌对环境中的使用，它们对使用在执行确定秘密密钥的算法期间观察到的信息的边信道攻击(sca)特别敏感。

ecc的最重要的运算是椭圆曲线点p与私人标量因素k的标量乘法。该运算常被标记为[k]p。其计算费用在ecc的总效率中是决定性的，然而实施sca对抗措施是非常消耗资源的。

图7是根据某些实施例的描绘椭圆曲线标量乘法(ecsm)方法的流程图。出于例示的目的，将参考蒙哥马利乘法做出图5的如下描述。

在步骤600中，可以接收私有密钥(标量k)和对ecsm乘积的请求，例如，对q＝[k]p的请求。底数点p被记为p＝(x，y)并且标量k被记为k＝(a，b)。参数n和rext也被接收或加载。

响应于接收到对ecsm乘积(q＝[k]p)的请求，如之前关于图2的步骤202描述的那样，在步骤602中选择扩展参数r。

在步骤604中，对曲线参数和底数点进行预处理。预处理包括替换每一个参数x、y、a和b，它们被转换成蒙哥马利形式：

-因此x被转换成

-因此y被转换成

-因此a被转换成

-因此b被转换成

在步骤606中，使用蒙哥马利乘法函数代替常规的蒙哥马利乘法来计算ecsm

因此该方法接收椭圆曲线上的底数点p和标量k(表示秘密标量)，底数点p具有素数阶，并生成随机整数。

然后可以在为的蒙哥马利表达式中使用蒙哥马利乘法将标量乘法[k]p确定为：

可以使用传统ecsm算法，使用点的两倍和两个不同点的加法来计算ecsm。

在步骤608中，可以进一步应用后处理以将乘积从蒙哥马利形式转换回常规形式。这包括通过应用蒙哥马利乘法运算符将第一分量转换成xq并将分量转换为yq，如下：

在步骤609中，从xqext和yqext确定分量xq和yq，根据：

xq＝xqextmodn

yq＝yqextmodn

从标量乘积乘积q＝(xq，yq)可以在步骤310中发布给请求应用程序。

本发明的益处是通过选择的随机数字代替使用常规模数来扩展“模数”，常规模数存在于固定数量的机器字(即，其大小是机器字长的倍数)，其易于利用“额外约简”进行攻击。扩展模数的使用允许对计算进行伴随的完整性检查，约简或甚至取消额外约简(例如对rsa)。在ecc计算(算法ecdbl&ecadd)中，由于在根据本发明的蒙哥马利模乘方法期间吸收了加法/减法中的约简，这样的运算可以被丢下或重新安排。

将在下文中描述没有约简的蒙哥马利模乘方法的示例性应用，考虑模数p和基数r的值，r等于：

这种基数r等于大于n的2的较小幂的2^α倍。

基数r满足下列不等式：

2^α≤r≤2^α+1n，

应注意，在下界中的上面的不等式仅仅在n是2的幂的情况下发生。如果n是素数或合成rsa数，则该不等式永不被满足。

发明人已经证明，取决于参数值α＞0，蒙哥马利模乘可以在没有额外约简的情况下并且针对参数α的一些值来实施。额外约简的缺失允许替代地执行额外加法。具体而言，它被确定为：

-对于α≥1，蒙哥马利模乘可以在没有额外约简的情况下实施，并且

-对于α≥2，甚至数z可以被添加以使0≤z≤n-1而无需额外约简。

即使不限于这种应用，本发明的这种实施例对于基于混合坐标系(例如雅可比坐标)的椭圆密码系统具有特别的优势，并且其可以用于加密、解密、签名生成、认证等过程中。

考虑在韦尔斯特拉斯形式椭圆曲线e上的两个点p1和p2，p1和p2的和被定义为p3＝p1+p2。

当p1不同于p2时，计算p1+p2被称为椭圆曲线加法或者ecadd，并且当p1＝p2时计算p1+p2＝[2]p1被称为椭圆曲线加倍或者ecdbl。

执行椭圆曲线加法ecadd以通过翻转连接椭圆曲线上的点p1＝(x1，y1)和椭圆曲线上的点p2＝(x2，y2)的直线在x轴上的交叉点来获得点p3＝p1+p2＝(x3，y3)。

执行椭圆曲线加倍以通过翻转椭圆曲线上的点p1＝(x1，y1)处的切线在x轴上的交叉点来获得点p4＝[2]p1＝(x4，y4)。

标量乘法涉及针对有限域上的椭圆曲线、针对曲线上的点p、并针对整数(也被称为标量)d计算点[d]p＝p+p+...+p(相加d次)。标量乘法被表示为椭圆曲线加法和椭圆曲线加倍的组合。

椭圆曲线加法、椭圆曲线加倍、和标量乘法的计算是在有限域中的加法、减法、乘法、平方、和求逆的组合。在很多情况下，通过加法、减法和常数进行乘法的计算时间相对短于其它处理的计算时间且可被忽略。因此椭圆曲线加法、椭圆曲线加倍、和标量乘法的计算时间通常可以被估计为在有限域中的乘法、平方和求逆的计算时间的总和。

在这种示例性应用中，被标记为“ecadd”的椭圆曲线加法中的域乘法后面紧跟着被标记为“ecdbl”的椭圆曲线加倍中的域平方，即当计算m时，ecadd中的z3＝z1*z2*h后跟随着ecdbl中的z1⁴。应注意，z1⁴被计算为(z1²)²：

根据ecdbl，p3＝(x3，y3，z3)＝2p1可以被计算为：

x3＝t，y3＝-8y1⁴+m(s-t)，z3＝2y1z1，s＝4x1y1²，m＝3x1²+az1⁴，t＝-2s+m²

根据ecadd，p3＝(x3，y3，z3)＝p1+p2可以被计算为：

x3＝-h³-2u1h²+r²，y3＝-s1h³+r(u1h²-x3)，z3＝z1z2h，u1＝x1z2²，u2＝x2z1²，s1＝y1z2³，s2＝y2z1³，h＝u2-u1，r＝s2-s1

还存在后面紧跟着ecdbl中的域平方的ecdbl中的域乘法，即当计算m时，(2*y1)*z1＝z3后面紧跟着ecdbl中的z1⁴。

在本发明的这种应用中，保护存在于根据本发明的实施例的打破进行模数扩展的x1和x2之间的关联以使最终模数nr不满足机器字的倍数的大小的假设。于是r不选择为32或64比特的倍数，不像常规方法(例如arashhariri和arashreyhani-masoleh的文章“oncountermeasuresagainstfaultattacksontheellipticcurvecryptographyusingfaultdetection”，“faultanalysisincryptography”，2012，springer)中做的那样。这允许使用基数r的所有比特。

在上面的ecbl和ecadd等式中，项u1h2-x3包含u1h2的乘法和在该乘法后的-x3的加法，其中0≤-x3＜n，假定x3是仿射坐标中的一个点的坐标。

根据本发明的实施例的蒙哥马利模乘方法去除了对额外约简的需要，于是节省的计算资源被重新用于执行附加的运算，例如加法。

根据本发明的实施例的蒙哥马利模乘方法在伪代码中根据下列算法可以被写为：

input：0≤x，y≤2^α-1n-1

output：(xyr^-1modn)+λn，forsome

1.c←ab

2.d←(-cn^-1)modr

3.e←c+dn//emodr＝0

4.f←e/r

5.returnf

应注意，该算法的cios(即粗集成运算数扫描)实施是特别有效的。

根据本发明的实施例的蒙哥马利模乘方法的内部变量c、d、e、f的下列区间值被认为是：

-0≤c≤(2^α-1n-1)²，

-0≤d≤r-1，

-0≤e≤(2^α-1n-1)²+n(r-1)，

-

为去除对额外约简的需求，模乘的结果f与该蒙哥马利模算法的输入中的条件相匹配，以使f也满足：

0≤f≤2^α-1n-1

同时f也满足：

为验证条件足够的是：

事实上，r满足等于下式的不等式r≥2^α-1n：

-r(2^α-1n-1-n)≤-2^αn(2^α-1n-1-n)

因此可以满足条件如果：

(2^α-1n-1)²-n-r(2^α-1n-1-n)≤(2^α-1n-1)²-n-2^αn(2^α-1n-1-n)

上述等式的右手边值可以被重新写为如下：

(2^α-1n-1)²-n-2^αn(2^α-1n-1-n)＝2^2α-2n²+1-2^αn-n-2^2α-1n²+2^αn+2^αn²

＝1-(2^2α-2+2^α)n-n

因为n＞1，上述等式的右手边值为负。条件相应的被满足。

通过在蒙哥马利模乘算法n的最后一步之后添加一个进一步的加法f+z，使得数z被添加到f，其中0≤z≤n-1，条件被重新写为如下：

(2^α-1n-1)²+n(r-1)+r(n-1)≤r×(2^α-1n-1)

该等式可以被重新写为：

这种条件被验证，如果：

应注意：

对于α＝3，-2^2α-2+2^α+1＝0且

对于α＞3，量-2^2α-2+2^α+1严格为负。

相应地，如果条件和被验证，则可以在没有额外约简的情况下容许仿射坐标中的一个进一步的加法，例如加法，以例如根据图1计算包含-x3的加法的项u1h2-x3。

该保护方法使得可以通过选择性地对模数“调整尺寸”以使额外约简的作用不是泄漏关于运算顺序的信息来将该实施移出攻击暴露的范围。

进一步地，还可以在指数运算期间应用重新堵塞的步骤，尽管这种堵塞通常仅在指数运算的输入处进行。

本发明还提供了一种用于保护密码系统100免受不同类型的攻击(例如，当系统100使用根据本发明的某些实施例的蒙哥马利模乘方法时，对有限域上的常规指数运算的攻击)的保护方法。这种攻击是基于可以确定乘法(或平方)的结果是否提供(或不提供)平方的事实。例如，考虑到能在一系列的算术运算中跟踪数据的攻击，注意，特别是具有非常高的相关性(绝对值大概在15％至30％)，如果来自乘法的结果被提供给平方运算，则可以确定攻击，如h.sato，d.schepers和t.takagi(2005)，“exactanalysisofmontgomerymultiplication”，progressincryptology-indocrypt2004，lecturenotesincomputerscience，出版商：springerberlin，第3348卷，第1387-1394页中所描述。

本发明的各种实施例允许一种计算通过以标称值p为模约简结果来获得正确答案，并通过以其它因素r为模约简结果来获得校验和。

各种实施例也允许与存储器字一致。

本发明提供防范若干攻击的保护，包括：

-时序攻击，因为模乘在常数时间内被执行而无需有条件约简，该有条件约简通常是若干攻击的基础；

-归因于允许检查计算的冗余的故障注入攻击；

应注意，可以在任何密码系统(例如rsa，ecc)中实施本发明。另外，一种互补验证方法可以用于某些应用中的故障检测。

具体而言，本发明适用于保护非对称密码系统以免受到故障注入攻击，如在“faultanalysisincryptography”(marcjoye和michaeltunstall，springerlncs，2011，doi：10.1007/978-3-642-29656-7；isbn978-3-642-29655-0)中所述的。例如，它阻止攻击者使用一个故障破坏密码系统(例如当利用中国剩余定理最优化时攻击者使用贝尔通信研究中心攻击rsa)。这也提供了针对使用一个故障泄露密钥的一个比特的其它故障攻击的保护，例如ecc上的安全误差。

本发明在用于在嵌入式系统(例如智能卡)中实施的密码系统、以及用于在m2m平台或在lot架构(物联网)的终端中实施的密码方案这二者的转换通道(数据泄漏)移除和故障注入的抵抗方面具有重大影响。

对于那些本领域技术人员来说其它的益处和修正将很容易地显现。因此本发明的更广阔的方面不限于所示出并描述的具体细节、代表性的方法和示例性的示例。相应地，可以偏离这种细节而不脱离申请人的总发明构思的精神或范围。特别地，尽管本发明对蒙哥马利乘法引擎具有特别的优势，应注意，本发明当以简单方式实施时也适用于其它模乘引擎，例如常规上具有额外约简特征的巴雷特乘法引擎或者克里斯托弗乘法引擎。巴雷特和克里斯托弗模乘引擎是其它高效的模乘，对于它们来说，通过以特定表示的运算降低了约简成本。应注意，根据本发明在巴雷特模乘引擎中的应用，模乘方法可以包括根据步骤206(a＝x1y-unr))的一个或多个减法。根据本发明在克里斯托弗模乘引擎中的应用，模乘方法仅包括根据步骤206(a＝x1y-unr))的一个减法。

本发明的实施例可以采取包含硬件和软件元件二者的实施例的形式。

此外，本文描述的密码学方法可以由被供应到计算机的任何类型的处理器的计算机程序指令实施，以产生具有执行该指令以实施本文规定的功能/动作的处理器的机器。这些计算机程序指令也可以存储在能够引导计算机以特定方式运行的计算机可读介质中。为此，计算机程序指令可以被装载到计算机中以引起一系列运算步骤的执行，并且由此产生计算机实施的过程，以使所执行的指令提供用于实施本文规定的功能/动作的过程。