一种新型四维超混沌系统的制作方法

发明涉及一种非线性系统的电路，特别是一种新型四维超混沌系统的电路。

背景技术：

上世纪，Lorenz发现了第一个经典的三维自治混沌系统，就此引起众多混沌研究者的关注，并且由此发现了许多新的三维混度系统，如Chen系统、L系统等等，这些混沌系统是三维的并且只有一个正的Lyapunov指数，所以在许多工程应用中经常被破解，例如在加密系统中，利用带宽相对较窄的三维自治混沌系统生成的序列来对信号进行加密，很容易通过滤波系统给予滤除，使其失去了加密的意义，因此，本发明提出一种新型四维超混沌系统，因为超混沌系统具有两个及两个以上正的Lyapunov指数，动力学行为比一般混沌系统更复杂，难以预测，在保密通信及信息安全等领域中具有更高的实用价值，同时在许多众多学科领域有着极大的研究意义和实用价值。

技术实现要素：

1.一种新型四维超混沌系统，其特征在于：该电路由四路电阻、电容、运算放大器(LF347BN)和乘法器(AD633JN)组成，所述电阻和运算放大器(LF347BN)组成加法电路和比例反相电路，所述电容和运算放大器(LF347BN)实现积分运算，乘法器(AD633JN)实现乘法运算；

第一路的同相输出端(x)接第三路的乘法器(A3)的一个输入端，接第四路的乘法器(A4)的一个输入端，第一路的反相输出端(-x)接第一路的反相加法电路的输入端，接第二路的乘法器(A2)的一个输入端，接第二路的反相加法电路的输入端，第一路的乘法器(A1)的输出端接第一路的反相加法电路的输入端，第二路的同相输出端(y)接第一路的反相加法电路的输入端，接第一路的乘法器(A1)的一个输入端，接第二路的反相加法电路的输入端，接第三路的乘法器(A3)的另一个输入端，第二路的反相输出端(-y)接第四路的反相加法电路的输入端，第二路的乘法器(A2)的输出端接第二路的反相加法电路的输入端；第三路的同相输出端(z)接第一路的乘法器(A1)的另一个输入端，接第二路的乘法器(A2)的另一个输入端，接第四路的乘法器(A4)的另一个输入端，第三路的反相输出端(-z)接第三路的反相加法电路的输入端，第三路的乘法器(A3)的输出端接第三路的反相加法电路的输入端；第四路的同相输出端(w)接第二路的反相加法电路的输入端，第四路的乘法器(A4)的输出端接第四路的反相加法电路的输入端。

有益效果：本发明提出一种新型四维超混沌系统，因为超混沌系统具有两个及两个以上正的Lyapunov指数，动力学行为比一般混沌系统更复杂，难以预测，在保密通信及信息安全等领域中具有更高的实用价值，同时在许多众多学科领域有着极大的研究意义和实用价值。

附图说明

图1为实现一种新型四维超混沌系统电路图。

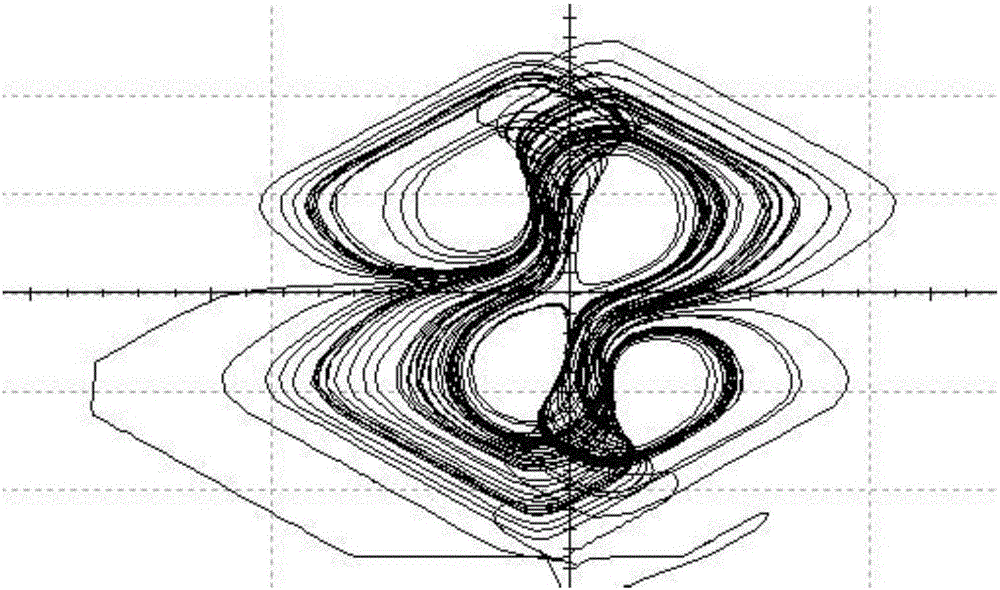
图2为一种新型四维超混沌系统产生xy象限的相图。

图3为一种新型四维超混沌系统产生xz象限的相图。

图4为一种新型四维超混沌系统产生xw象限的相图。

图5为一种新型四维超混沌系统产生yz象限的相图。

图6为一种新型四维超混沌系统产生yw象限的相图。

图7为一种新型四维超混沌系统产生zw象限的相图

具体实施方式

下面结合附图和优选实施例对本发明作更进一步的详细描述，参见图1-图7。

1.一种新型四维超混沌系统，其特征在于：该电路由四路电阻、电容、运算放大器(LF347BN)和乘法器(AD633JN)组成，所述电阻和运算放大器(LF347BN)组成加法电路和比例反相电路，所述电容和运算放大器(LF347BN)实现积分运算，乘法器(AD633JN)实现乘法运算；

第一路的同相输出端(x)接第三路的乘法器(A3)的一个输入端，接第四路的乘法器(A4)的一个输入端，第一路的反相输出端(-x)接第一路的反相加法电路的输入端，接第二路的乘法器(A2)的一个输入端，接第二路的反相加法电路的输入端，第一路的乘法器(A1)的输出端接第一路的反相加法电路的输入端，第二路的同相输出端(y)接第一路的反相加法电路的输入端，接第一路的乘法器(A1)的一个输入端，接第二路的反相加法电路的输入端，接第三路的乘法器(A3)的另一个输入端，第二路的反相输出端(-y)接第四路的反相加法电路的输入端，第二路的乘法器(A2)的输出端接第二路的反相加法电路的输入端；第三路的同相输出端(z)接第一路的乘法器(A1)的另一个输入端，接第二路的乘法器(A2)的另一个输入端，接第四路的乘法器(A4)的另一个输入端，第三路的反相输出端(-z)接第三路的反相加法电路的输入端，第三路的乘法器(A3)的输出端接第三路的反相加法电路的输入端；第四路的同相输出端(w)接第二路的反相加法电路的输入端，第四路的乘法器(A4)的输出端接第四路的反相加法电路的输入端。

当然，上述说明并非对发明的限制，本发明也不仅限于上述举例，本技术领域的普通技术人员在本发明的实质范围内所做出的变化、改型、添加或替换，也属于本发明的保护范围。