一种Tate配对的实现方法及其电路结构与流程

本发明属于信息安全领域，涉及一种Tate配对的实现方法及其电路结构，可应用于公钥密码学领域。通过使用本发明，能够快速计算基于椭圆曲线或超椭圆曲线上的Tate配对，为基于属性加密系统、数字签名、密钥协议等公钥密码学方案提供了基础技术支撑。

背景技术：

椭圆曲线上的配对是具有特殊性质的映射，该映射将椭圆曲线点群中的两个点映射为扩域的乘法群中的某个元素，此处正整数k为嵌入次数，其取值与所选取的椭圆曲线相关。

假设G₁和G₂均为加法交换群，G_T为乘法循环群，记映射为e，则双线性配对映射e的定义如下：

e:G₁×G₂→G_T

且对于任意的P,P₁,P₂∈G₁和Q,Q₁,Q₂∈G₂，满足以下条件

(1)双线性：

e(P₁+P₂,Q)＝e(P₁,Q)e(P₂,Q)，e(P,Q₁+Q₂)＝e(P,Q₁)e(P,Q₂)

(2)非退化性：对于任意的P∈G₁\{0}，存在Q∈G₂，使得e(P,Q)≠1；对于任意的Q∈G₂\{0}，存在P∈G₁，使得e(P,Q)≠1。

(3)可计算性：存在有效的算法(多项式时间算法)可以计算映射e。

双线性配对的安全性是基于双线性计算性Diffie Hellman困难问题假设(BCDHP假设)，即给定P,aP,abP∈G₁，计算bP且满足e(P,P)^b∈G₂，其中为未知数。同时，对于任意的多项式时间攻击者A而言，三元组(aP,abP,bP)和(aP,abP,R)在计算上是不可区分的，其中R为G₁中的一个随机数。即不存在任何有效的概率多项式时间算法满足：

|Pr[D(aP,abP,bP)＝1]-Pr[D(aP,abP,R)＝1]|>1/q

假设E为一条定义在F_p上的椭圆曲线。椭圆曲线E上的点群记为E(F_p)，是一个有限群。椭圆曲线E在F_p上的点的个数就是点群的阶，使用#E(F_p)来表示。椭圆曲线E上点记为P，无穷远点记为O。定义l为满足lP＝O的最小整数，称为点P的阶。椭圆曲线E上点P分为两类：存在有限阶的点(挠点)和无穷阶的点。无穷阶的点意味着无法通过累加自身的值得到无穷远点O。如果挠点P的有限阶为l，则称其为l-挠点。定义r为#E(F_p)的最大质因数，k为椭圆曲线E的嵌入度，满足r|q^k-1。

令G₁＝E(F_q)[r](G₁＝<P>，P为挠点)，为的零轨迹子群)，G_T＝μ_r(μ_r为扩域上的单位根)，则本发明所使用的Tate配对定义为：

利用不同的代数曲线可以构造出不同形式的双线性配对，而不同的代数曲线所能提供的安全性和计算效率不同。本发明所涉及的Tate配对，是由基于256位素数域上嵌入度k＝12的BN曲线(Barreto-Naehrig curves)所构成的，可以提供超过128位的安全性。

本发明所使用的BN曲线下Tate配对的映射t_r表示为：

目前Tate配对的算法没有较快的硬件实现方案，计算的步骤比较复杂，计算过程需要大量的时间，严重制约了双线性配对在信息安全领域的应用；因此设计较快的计算算法，保证硬件加速设计的合理的性能面积比，成为了一个亟待解决的问题。

技术实现要素：

为了克服现有技术中存在的技术问题，本发明的目的是设计一种Tate配对的实现方法及其电路结构。

实现上述目的所采用的解决方案为：

1、一种Tate配对算法的硬件实现，包括：

利用BN曲线的域扩张的特点，将和下的运算化简为F_p下的运算。根据化简后运算的特点，设计了一种可以进行F_p和两种模式下的加法、减法、乘法、求逆运算的计算单元。当配置为F_p下的计算模式时，1个计算单元可以同时独立计算3次F_p下的加法、减法、乘法和1次求逆运算；当配置为下的计算模式时，可以计算1次下的加法、减法和乘法运算。

Tate配对算法的电路结构包括多个模块，包含了存储模块、计算单元、待计算数据选择器、中间结果数据选择器、访问控制模块、指令控制模块，能够快速计算由BN曲线构成的Tate配对。存储模块，用来存储Tate配对的初始值、预算值和计算的中间结果。计算单元，根据其配置的不同，可以进行F_p下的加法、减法、乘法、求逆运算和下的加法、减法、乘法运算。待计算数据选择器，输入为存储模块的输出，输出为2个计算单元的输入。中间结果数据选择器，输入为2个计算单元的输出，输出为存储模块的输入。访问控制模块，可以通过控制中间结果数据选择器和待计算数据选择器来控制数据的流动。指令控制模块，中存储了配置计算单元和访问控制模块的指令，对整个Tate配对的计算的过程进行控制。

2、一种Tate配对算法，包括：

Tate配对的计算分为“倍点操作”、“加点操作”、“最终模幂”三个部分，计算过程如下：对Tate配对的输入P点和Q点的坐标转换后，通过待计算数据选择器进入计算单元。将二进制的形式表示的r除去最高位，从高位到低位依次遍历判断每一位。如果为0，则执行“倍点操作”；如果为0，则先后执行“倍点操作”和“加点操作”。当二进制的形式表示的r遍历完毕后，进入最后模幂的计算。控制指令模块根据执行的操作不同，控制待计算数据选择器的选择存储模块中的数据进入计算单元，指定计算单元的计算模式，并且通过控制中间结果数据选择器将计算单元的计算结果存储到存储模块的不同位置。Tate配对的计算过程需要反复重复此过程，Tate配对算法调度方案运行完毕后得到最终的计算结果。

由于F_p下的乘法、求逆运算的时间要远大于F_p下的加法、减法运算，指令控制模块的设计需要考虑2个计算单元的均衡，避免其中一个计算单元在完成运算后，浪费大量时间等待另一个计算单元的情况。可以通过调度Tate配对所需的计算，尽量把乘法、求逆运算的操作平均分配给2个计算单元。

与现有技术相比，本发明的积极效果为：

本发明从减少循环次数、降低计算复杂度的角度出发，能够快速计算出Tate配对，具有较强的可移植性和单元复用性，并且保证Tate配对计算的正确性。

附图说明

图1为本发明提供的计算单元硬件结构图；

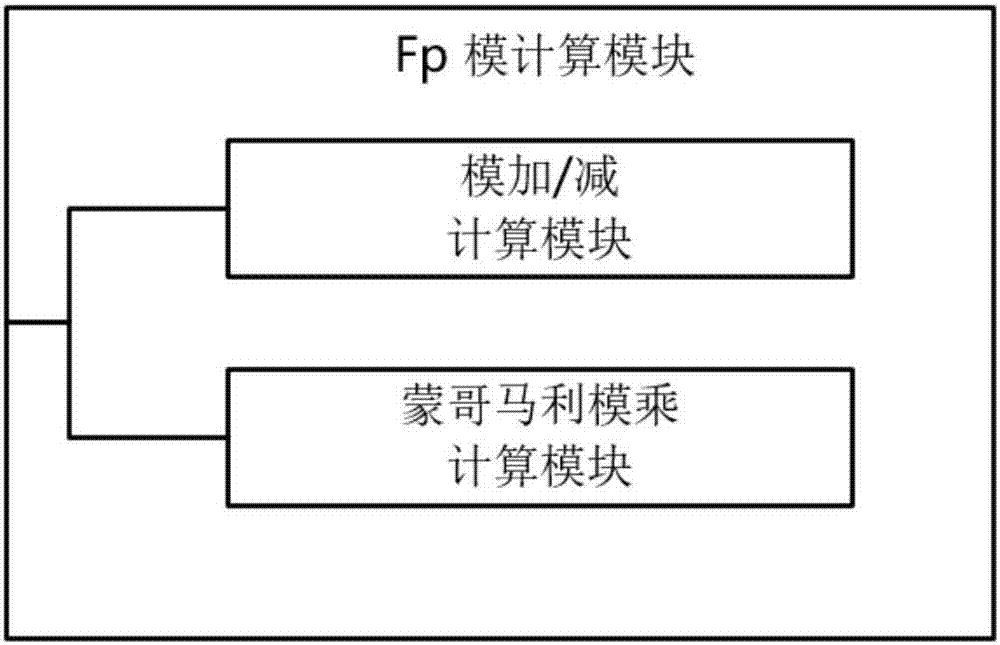
图2为本发明提供的F_p模计算模块硬件结构图；

图3为本发明提供Tate配对算法调度方案的硬件实现的体系结构图。

具体实施方式

以下结合实施例和附图对本发明进行详细说明，但不构成对本发明的限制。

本发明所涉及的Tate配对，是基于素数域上嵌入度k＝12的BN曲线所构成的，同时由于BN曲线是六次扭曲(d＝6)，意味着有很多在扩域上的计算可以规约到扩域上，使得其计算效率较高。本发明所涉及的BN曲线的形式如下：

E/F_p:Y²＝X³+b，

根据给定的整数z，可以得到素数p＝36z⁴+36z³+24z²+6z+1。BN曲线为有限域上的椭圆曲线，BN曲线上的点群记为记为点群元素的数量记为阶r＝#E(F_p)，素数r＝36z⁴+36z³+18z²+6z+1。记BN曲线在有限域上的迹为整数t＝p-r+1＝6z²+1。

本发明所涉及的BN曲线下Tate配对的映射表示为：

其中P为BN曲线上的挠点，Q为的零轨迹子群中映射在有限域上的点。

本发明计算Tate配对时所使用的算法如算法1和算法2所示：

步骤1：将阶r用二进制的形式表示，将仿射坐标的点P和Q转换为Jacobian坐标。记f_r,p(Q)为f，其初始值为1。f_r,p(Q)是一个和r、P点、Q点有关的函数值。

步骤2：如算法1所示，计算f_r,p(Q)，此步骤类似椭圆曲线加密算法中常见的Miller算法。将二进制表示的r，其二进制的位数为L，除去最高位，从高位到低位依次遍历每一位。如果遍历的当前位为0，则只需进行“倍点操作”，如果遍历的当前位为1，则需进行“倍点操作”和“加点操作”。“倍点操作”的过程为：计算倍点2T，点Q在过点T切线上的值l_T,T(Q)，f²和f²·l_T,T(Q)。“加点操作”的过程为：计算加点T+P，过点T和P切线上的值l_T,P(Q)，f·l_T,P(Q)。步骤2的计算涉及和下的加法、减法、乘法、求逆运算，经过L-1次循环后(即算法1中的for i from L-2downto 0)，最终得到该阶r的f_r,p(Q)。

算法1：计算f_r,p(Q)

步骤3：如算法2所示，计算其中f为步骤2经过Miller算法得到的f_r,p(Q)的简写，此步骤也被称作最终模幂运算。步骤3的计算涉及下的加法、减法、乘法、求逆运算，最终得到Tate配对t_r(P,Q)。

算法2：计算

b←a^p，b←a·b

4、计算f^p，

6、计算T^z，(T^z)^6z

7、T←(T^z)^6z·T

本发明所涉及的BN曲线所在的扩域可以通过多次的塔域扩张构造，在F_p基础上进行二次扩张得到扩域然后在基础上进行三次扩张得到扩域最后在基础上进行二次扩张得到扩域扩域和的构造如表1所示，其中X,Y,Z∈F_p：

表1扩域的表示

根据计算Tate配对时所使用的算法1可知，计算涉及和下的加法、减法、乘法、求逆运算。如果分别针对每个运算使用单独的模块进行计算，会造成本发明所涉及的Tate配对的硬件实现规模十分庞大，且模块的利用率低，浪费大量的硬件资源。利用表1所示的BN曲线所在的扩域的多次塔域扩张构造方法，可以对和下的运算进行化简，最终归约为F_p和下的运算，进一步节省中间计算的存储资源。针对大量使用到的F_p和下的运算，本发明提出一种计算单元的设计。

本发明所涉及的计算单元由3个相同的F_p模计算模块和1个F_p模逆计算模块组成，其硬件结构如图1所示。计算单元中的F_p模计算模块可以执行F_p下的加法、减法、乘法计算，F_p模计算模块的硬件结构如图2所示。在这里F_p模计算模块的乘法计算使用的是蒙哥马利算法，F_p模逆计算模块的求逆计算使用的是欧几里得算法。当素数p的位数很大时，计算F_p下乘法、求逆的时间要远大于计算加法、减法的时间。在本发明专利中，记1个F_p模计算模块在计算F_p下乘法的时间为m，1个F_p模逆计算模块在计算F_p下求逆的时间为i。

本发明涉及的计算单元可以被配置为2种计算模式，分别为F_p和下的运算。当配置为F_p下的计算模式时，所述计算单元中的F_p模计算模块和F_p模逆计算模块独立进行计算，1个计算单元可以分别独立计算3次F_p下的加法、减法、乘法，或1次求逆运算；当配置为下的计算模式时，所述计算单元同时调用三个F_p模计算模块进行运算，1个计算单元可以计算1次下的加法、减法和乘法运算。

下的乘法c＝a×b的计算规则如下(其中a＝a₀+a₁X，b＝b₀+b₁X，c＝c₀+c₁X，a₀,a₁,b₀,b₁,c₀,c₁,X∈F_p)：

v₀＝a₀b₀,v₁＝a₁b₁

c₀＝v₀+βv₁

c₁＝(a₀+a₁)(b₀+b₁)-v₀-v₁

根据下的乘法c＝a×b的计算规则，计算1次下的乘法运算需要计算3次F_p下的乘法，通过算法的合理排序，将3次F_p下的乘法分配在同一时间，可以有效避免本发明所涉及的计算单元中的某个F_p模计算模块在执行F_p下加法、减法运算的完成运算后，浪费大量时间等待执行其他F_p模计算模块执行F_p下乘法运算。根据合理排序后的算法，1个计算单元在计算1次下乘法，需要的计算时间近似为m，与1个F_p模计算模块在计算F_p下乘法的时间相同。类似的，1次下的平方运算需要计算2次F_p下的乘法，但是由于计算单元的硬件结构，需要的计算时间近似为m。

为了计算本发明涉及的Tate配对，在算法1、2的基础上，设计了一种包含了存储模块、计算单元、待计算数据选择器、中间结果数据选择器、访问控制模块、指令控制模块的硬件结构，能够快速计算由BN曲线构成的Tate配对。本发明涉及的Tate配对算法的硬件结构如图3所示：

所述存储模块，用于存储Tate配对的输入、预算值和计算的中间结果，由50个256位寄存器组成。所述计算单元，用于根据所述指令控制模块发送过来的配置指令进行F_p下的加法、减法、乘法、求逆运算和下的加法、减法、乘法运算；并将计算结果发送给所述中间结果数据选择器。每个计算单元的输入为6个256位，输出为3个256位。所述待计算数据选择器，用于根据所述访问控制模块的指令从所述存储模块中读取数据，并将其发送给所述计算单元。所述中间结果数据选择器，用于根据所述访问控制模块的指令将收到所述中间结果数据发送给所述存储模块；所述访问控制模块，用于根据所述指令控制模块发送过来的控制指令，控制所述中间结果选择器和所述待计算数据选择器的数据流动。所述指令控制模块，用于存储Tate配对算法的控制指令和配置指令，对整个Tate配对的计算的调度过程进行控制。

本发明所涉及的Tate配对分为“Miller函数”部分(如算法1所示)和“最终模幂”部分(如算法2所示)，其中“Miller函数”部分主要包含“倍点操作”、“加点操作”。因此在分析本发明涉及的Tate配对的计算时，分为“倍点操作”、“加点操作”、“最终模幂”三个部分来描述指令控制模块分配2个计算单元的过程。计算过程如下：Tate配对的输入P点和Q点的坐标转换后，存储在存储模块中，通过待计算数据选择器进入计算单元。将二进制的形式表示的r除去最高位，然后从高位到低位依次遍历判断每一位。如果为0，则本发明所实施的电路结构执行“倍点操作”；如果为1，则本发明所实施的电路结构先后执行“倍点操作”和“加点操作”。当二进制的形式表示的r遍历完毕后，进入最后模幂的计算。访问控制模块根据执行的操作不同，控制待计算数据选择器的选择存储模块中的数据进入计算单元，指定计算单元的计算模式，并且通过控制中间结果数据选择器将计算单元的计算结果存储到存储模块的不同位置。Tate配对的计算过程需要反复重复此过程，直到二进制的形式表示的r遍历完毕，Tate配对算法调度方案运行完毕后得到最终的计算结果。

指令控制模块是计算Tate配对过程的核心。由于F_p下的乘法、求逆运算的时间要远大于F_p下的加法、减法运算，指令控制模块的设计需要考虑2个计算单元的均衡，避免其中一个计算单元在完成运算后，浪费大量时间等待另一个计算单元的情况。可以通过调度Tate配对所需的计算，尽量把乘法、求逆运算的操作平均分配给2个计算单元。

本发明涉及的Tate配对的输入P点和Q点，分别表示如下：

P＝(X,Y,Z)，其中Z＝1，X,Y,Z∈F_p

Q＝(x,y)＝(x₁·u+x₀,y₁·u+y₀)，其中x₀,x₁,y₀,y₁,u∈F_p

(1)倍点操作的计算

倍点操作涉及和下的加法、减法、乘法运算，具体包括计算倍点2T，点Q在过点T切线上的值l_T,T(Q)，Miller函数的平方f²，最终得到新的Miller函数值f²·l_T,T(Q)。

在Jacobian坐标系下，T点表示为T＝(X₁,Y₁,Z₁)，X₁,Y₁,Z₁∈F_p，Q点表示为Q＝(x,y)，则倍点2T表示为2T＝(X₃,Y₃,Z₃)，其中：

过点T切线上Q点的值为

在计算2T＝(X₃,Y₃,Z₃)和l_T,T(Q)时只需要F_p和下的加法、减法、乘法计算，且不需要F_p下的求逆计算。使用1个计算单元计算2T＝(X₃,Y₃,Z₃)和l_T,T(Q)，如果将计算过程在1个计算单元中的3个F_p模计算模块中合理分配，只需要6m的时间。

计算f²的时候，涉及下的平方运算，此时γ为表1中的符号，其计算公式如下：。

v＝f₀·f₁

c₀＝(f₀+f₁)(f₀+γf₁)-v-γv

c₁＝2v

在这里v,c₀,则计算1个下的平方，需要2个下的乘法。进一步化简下的乘法c＝a×b，其计算公式如下(在这里a₀,a₁,b₀,b₁,c₀,c₁,)：

v₀＝a₀b₀,v₁＝a₁b₁,v₂＝a₂b₂

c₀＝v₀+ξ[(a₁+a₂)(b₁+b₂)-v₁-v₂]

c₁＝(a₀+a₁)(b₀+b₁)-v₀-v₁+ξv₂

c₂＝(a₀+a₂)(b₀+b₂)-v₀+v₁-v₂

在计算下的乘法只涉及下的加法、减法、乘法运算，且不需要F_p下的求逆计算。使用1个计算单元计算下的乘法，需要6m的时间；如果使用1个计算单元计算下的乘法，只需要3m的时间。

在本发明的实施例中，将下的平方运算中的计算v＝f₀·f₁的部分和计算2T＝(X₃,Y₃,Z₃)和l_T,T(Q)分别并行使用1个计算单元，计算开销为6m时间。将下的平方运算中的剩余部分使用2个计算单元，计算开销为3m时间。因此计算2T＝(X₃,Y₃,Z₃)，l_T,T(Q)和下f²，共需要的时间开销为9m。

l_T,T(Q)可以表示为(l₀+l₁v)+(l₂v)w的形式，其中l₀∈F_p，根据塔域扩张的构造，可以得到f·l_T,T(Q)＝[(f_0,0+f_0,1v+f_0,2v²)+(f_1,0+f_1,1v+f_1,2v²)w]·[(l₀+l₁v)+(l₂v)w]，涉及下的加法、减法、乘法运算，且不需要F_p下的求逆计算。使用Karatsuba算法来计算1次下的乘法需要18次F_p下的乘法运算，但是由于l_T,T(Q)的表示形式，只需要14次或9次F_p下的乘法运算。因此f·l_T,T(Q)计算使用2个计算单元，计算开销为7m时间。

因此，倍点操作的计算开销为16m时间。

(2)加点操作的计算

倍点操作涉及和下的加法、减法、乘法运算，具体包括计算加点T+P，点Q在过点T和P割线上的值l_T,P(Q)，最终得到新的Miller函数值f·l_T,P(Q)。

在Jacobian坐标系下，T＝(X₁,Y₁,Z₁)，P＝(X₂,Y₂)，则加点T+P＝(X₃,Y₃,Z₃)，其中：

点Q在过点T和P割线上的值

在计算T+P＝(X₃,Y₃,Z₃)和l_T,P(Q)时只需要F_p和下的加法、减法、乘法计算，且不需要F_p下的求逆计算，使用2个计算单元的开销为5m时间。

计算f·l_T,P(Q)的方式和f·l_T,T(Q)相同，使用相同的指令，因此使用2个计算单元，计算开销为7m时间。

因此，加点操作的计算开销为12m时间。

(3)最终模幂的计算

最终模幂的计算即其中(p¹²-1)/r可以化简为(p⁶-1)×(p²+1)×[(p⁴-p²+1)/r]，因此计算最终模幂的算法如算法2所示。

的计算，其中f＝f₀+f₁w，利用塔域扩张的特性和共轭的性质，只需要进行1次下的减法运算。f^-1的计算，即下的求逆运算，需要将f^-1＝(f₀+f₁w)^-1，化简如下(其中γ如表1所示)：

t₁＝(f₀)²,t₂＝(f₁)²,t₃＝t₁-γt₂

(f₀+f₁w)^-1＝(f₀-f₁w)/t₃

注意到1次下的求逆运算，经过分解后，还包括一次下的求逆运算，需要继续分解计算。当a＝a₀+a₁Y+a₂Y²，其中则a^-1化简如下(ξ如表1所示)：

A＝(a₀)²-ξa₁a₂，B＝ξ(a₂)²-a₀a₁，C＝(a₁)²-a₀a₂

F＝ξa₁C+a₀A+ξa₂B

(a₀+a₁Y+a₂Y2)^-1＝(A+BY+CY²)/F

注意到1次下的求逆运算，经过分解后，还包括一次下的求逆运算，需要继续分解计算。当a＝a₀+a₁X，其中a₀,a₁∈F_p，则化简如下(β如表1所示)：

t₁＝(a₀)²,t₂＝(a₁)²，t₃＝t₁-βt₂

最终将1次下的求逆运算，化简为F_p下的求逆运算，可以使用2个F_p模逆计算模块进行计算。最终的计算使用2个计算单元，通过复杂的分配过程，计算开销为26m+i时间。

本发明实施例指定的BN曲线的参数z＝6000000000001F2D(16进制表示)。根据给定的z，可以得到256位的素数p＝36z⁴+36z³+24z²+6z+1，其汉明重量为87。BN曲线上的点群的阶r＝#E(F_p)，为256位的素数r＝36z⁴+36z³+18z²+6z+1，其汉明重量为91。记BN曲线在F_p上的迹为128位整数t-1＝p-r＝6z²+1，其汉明重量为28。因此在“Miller函数”部分中，循环了255次，其中“倍点操作”进行255次，“加点操作”进行90次。本发明涉及的Tate配对的计算的分配和计算开销总结如表2所示：

表2 Tate配对的计算步骤的开销

实施例1：给定P点(P_x,P_y)，Q点(Q_x0+Q_x1X,Q_y0+Q_y1X)，其参数如下：

px＝256'h2143C691B939B083FA432FC11029B2C86419AD996EF3A9F18D8BB21EF0FAA579；

py＝256'h0143C3B68566CF29320AAC944ED681BF637EBF03C9D7BDE500BC7F3C4A4A96A6；

qx0＝256'h00C98F7F98435DA150E2CA69E424F4B01690FFE458DF62BF7126B522A9E0A3DE；

qx1＝256'h094939C9638F88F3BF29CAAF2AE0E47CE3A7AC7CDE48372283996846363DE23B；

qy0＝256'h02891DD88F3DCF1983A81E0DDD0C4727F008FE10FAEC54B5663D529E0489510C；

qy1＝256'h03A29EAD0874C26E9E0E9195F54089F0CB77791252D1ED496225D0772AAD87DB；

经过本发明涉及的一种Tate配对算法的调度方案及其硬件实现，得到t_r(P,Q)，其结构如下：

t_r(P,Q)＝{[(f121,f120),(f111,f110),(f101,f100)],{(f021,f020),(f011,f010),(f001,f000)]}

f000<＝`TD 256'h2031e4e671cdb52414589124a98b72720010f92054808a252ad5f7936e9f6bee；

f001<＝`TD 256'h07c8777f8f6a138b075d25b0eed2c7db6d04882dc2df922b8e99e6b19e5b3ee3；

f010<＝`TD 256'h211c3d1aa60ce0f2843efe8451a68def9a8b81825e5100e38858b5fbf10fcbb7；

f011<＝`TD 256'h0060c96b240747adb2b80f4809486dba1f8e46dc232e13662f783645e4fa3136；

f020<＝`TD 256'h21ec35365bc32b17b0917a258f8bf6938437ad766550684f314b39aaeaf5467b；

f021<＝`TD 256'h16ef01ba1de023aeb1d12ab79c412b18a99d805ec8e6120bdf4017e985d9be8b；

f100<＝`TD 256'h22c8a1da6113d7acc2479798ed95983f278a039563d700348d51a1a6b3b9f38e；

f101<＝`TD 256'h06bf6d607b4e12c6e3e2b7eb645a38c12bb7f512114da0df585954c8e5c4ed75；

f110<＝`TD 256'h064f0663ef6fdae79f3408838142bd2252d141d9a75b6a8df5d7a10824bb7736；

f111<＝`TD 256'h14114b44012f864e47695d699a8329af0984cbcfe7faa92da4b4fdc002294bd9；

f120<＝`TD 256'h1f67eadf2c91c8d0d16cb86599161196d19882cfebc56e4bcb09da29085e6c10；

f121<＝`TD 256'h0b2ec8c65440771a0c4ba14a791ac4bed71b146df7472d3d1318d800adc712c3；

t_r(P,Q)⁶的计算结果如下：

f000<＝`TD 256'h21ae1b053aa1cc642460200a76b816eb4bbf8297572823f5d3d17dd3d68eb6f7；

f001<＝`TD 256'h0282cb0db37a24bd1863e43933cf17ea5a6b5b4da4c19fd3ab5b3eb550981995；

f010<＝`TD 256'h17cfb9c563d74abb273367868805a7dc44d4574a8cb4ec9279946775cbdf266c；

f011<＝`TD 256'h0076bd18b770f4ac51f7ae63e45e224c0ee24d7a6a47ce184de2c9dd44d46257；

f020<＝`TD 256'h02c83ea01204be61d53307a127271ece378d92ce22acb17b67c103f69af2bdec；

f021<＝`TD 256'h13ff7ba1e40effba213b5346dd91e089b7391e91ed750ea6380e808cca4c06a5；

f100<＝`TD 256'h1c800b055f15f265172c9034eb2a467cb7651d9686e0f07017f397c92264595e；

f101<＝`TD 256'h193a925f7d2a8023441ff0f88c844a76717bdffbbc06259f73200dd67def3c5c；

f110<＝`TD 256'h23c8b3b3cc394b67567ce984285fb1d4c343a720747e3a3c61c4b29fb4d93b10；

f111<＝`TD 256'h1cda93571d14132ae8275ff6c3666065a7ae9af0c3675c33663e8607c7ebe4c9；

f120<＝`TD 256'h1ebf4311ed7403e5436edcaacbd3d90e8e886bac72fe393aed6bb4eb9b47452f；

f121<＝`TD 256'h14420203ac33c1a6991c2b1bf83ea67791d1c1c1c017b8fa949dbdc4b641255d；

t_r(2P,3Q)的计算结果如下：

f000<＝`TD 256'h21ae1b053aa1cc642460200a76b816eb4bbf8297572823f5d3d17dd3d68eb6f7；

f001<＝`TD 256'h0282cb0db37a24bd1863e43933cf17ea5a6b5b4da4c19fd3ab5b3eb550981995；

f010<＝`TD 256'h17cfb9c563d74abb273367868805a7dc44d4574a8cb4ec9279946775cbdf266c；

f011<＝`TD 256'h0076bd18b770f4ac51f7ae63e45e224c0ee24d7a6a47ce184de2c9dd44d46257；

f020<＝`TD 256'h02c83ea01204be61d53307a127271ece378d92ce22acb17b67c103f69af2bdec；

f021<＝`TD 256'h13ff7ba1e40effba213b5346dd91e089b7391e91ed750ea6380e808cca4c06a5；

f100<＝`TD 256'h1c800b055f15f265172c9034eb2a467cb7651d9686e0f07017f397c92264595e；

f101<＝`TD 256'h193a925f7d2a8023441ff0f88c844a76717bdffbbc06259f73200dd67def3c5c；

f110<＝`TD 256'h23c8b3b3cc394b67567ce984285fb1d4c343a720747e3a3c61c4b29fb4d93b10；

f111<＝`TD 256'h1cda93571d14132ae8275ff6c3666065a7ae9af0c3675c33663e8607c7ebe4c9；

f120<＝`TD 256'h1ebf4311ed7403e5436edcaacbd3d90e8e886bac72fe393aed6bb4eb9b47452f；

f121<＝`TD 256'h14420203ac33c1a6991c2b1bf83ea67791d1c1c1c017b8fa949dbdc4b641255d；

经验证t_r(2P,3Q)＝t_r(P,Q)⁶，这说明本发明涉及的一种Tate配对算法的调度方案及其硬件实现能够正确的计算Tate配对。