结合高斯过程与强化学习的服务组合方法与流程

本发明涉及一种利用计算机对Web服务组合的方法，属于人工智能领域。

背景技术：

随着计算机技术的发展，软件系统的需求越来越复杂多变，再加上互联网和信息技术的发展，逐渐催生出了一种面向服务的软件架构(Service-Oriented Architecture)：将实现了某些功能的软件或组件置于互联网的环境中作为web服务，用户可以通过某种消息协议和web服务通信，从而使用其功能。最后通过组合多种web服务，构建满足需求的新的软件系统。目前常见的web服务有天气服务，地图定位服务等等。

对于某一功能，一般会有不同服务提供者提供的功能类似，但服务质量(Quality of Service,QoS)有所差别的多个服务，能满足某功能的一类服务称为抽象服务，多个满足该功能的具体服务称为该抽象服务的候选服务。对于一个用户需求，如何从多个候选服务中选择出质量最优的服务，并且最终得出服务的最优组合，便是服务组合问题，根据不同服务的QoS属性来进行服务的选择和组合优化称为QoS感知的服务组合。由于互联网环境具有高度的动态性，某个服务的QoS属性可能会随着时间和环境的变化而发生波动或改变，因此服务组合方法需要具有一定的自适应性，能够应对环境变化带来的影响。同时，由于候选服务不断增多，业务需求也越来越复杂，一个复杂的用户需求往往包含多个抽象服务，以及相应的候选服务，因此服务组合方法也需要能够面对这种大规模服务组合问题的挑战。基于以上两点问题，部分学者提出了基于马尔科夫决策过程(Markov Decision Processes,MDP)和强化学习的服务组合方法。MDP是一种决策规划技术，在服务组合中，将当前网络环境和上下文建模为MDP中的状态，将当前状态下可供选择的多个候选服务建模为MDP中可进行的多个动作，在执行某个动作后，便转移到新的状态，从而进行下一轮的选择，直到最终完成整个服务组合。使用MDP模型对服务组合过程进行建模后，便可以将探索最优的服务组合问题转化为MDP模型的求解问题，从而进一步使用强化学习方法。强化学习方法是求解MDP模型的一种有效方法，尤其是在服务组合问题的大规模动态环境下，强化学习通过与环境的迭代交互进行学习，天然的具有自适应性，能够很好的应对网络环境下的服务组合问题。在传统强化学习算法Q-learning中，Q值通过值表记录，缺乏泛化能力，学习的结果也不够准确，受噪声影响较大。

技术实现要素：

发明目的：针对现有技术中存在的问题，本发明公开了一种结合高斯过程与强化学习的服务组合方法，使用高斯过程对Q值的学习进行建模，从而使其具有更好的精确性和泛化性。

技术方案：本发明采用的技术方案如下：

一种结合高斯过程与强化学习的服务组合方法，包括如下步骤：

(1)将服务组合问题建模为一个四元组马尔可夫决策过程；

(2)应用基于Q-learning的强化学习方法求解四元组马尔可夫决策过程，得到最优策略；

(3)将最优策略映射为web服务组合的工作流。

具体地，步骤(1)中将服务组合问题建模为如下四元组马尔可夫决策过程：

M＝<S,A,P,R>

其中S是环境中有限状态的集合；A是可调用的动作的集合，A(s)表示在状态s下可进行的动作的集合；P是描述MDP状态转移的函数，P(s′|s,a)表示在状态s下调用动作a后转移到状态s′的概率；R是回报值函数，R(s,a)表示在状态s下调用动作a所得的回报值。

具体地，步骤(2)应用基于Q-learning的强化学习方法求解四元组马尔可夫决策过程，得到最优策略，包括如下步骤：

(21)将状态动作对z＝<s,a>作为输入，对应的Q值Q(z)作为输出，建立Q值高斯预测模型；

(22)初始化Q-learning中学习率σ，折扣率γ，贪心策略概率ε，当前状态s＝0，当前时间步长t＝0；

(23)用概率为ε的贪心策略选择一个服务a作为当前服务a_t并执行，

(24)记录在当前状态s_t下执行当前服务a_t的回报值r_t和执行服务a后的状态s_t+1；根据下式计算在状态动作对z_t＝<s_t,a_t>下的Q值：

其中Q(z_t)为在状态动作对z_t＝<s_t,a_t>下的Q值，σ为学习率，r为回报值，γ为折扣率，s_t+1为执行服务a_t后从当前状态s_t转移到的后继状态，a_t+1为在状态s_t+1下选择的服务，Q(s_t+1,a_t+1)表示在状态动作对<s_t+1,a_t+1>下的Q值；

(25)按照高斯预测模型更新Q值：

其中I为单位矩阵，ω_n为不确定性参数，Z为历史状态动作对的集合，为与Z对应的历史Q值的集合，K(Z,Z)为历史状态动作对之间的协方差矩阵，其第i行j列元素为k(z_i,z_j)，k(·)为核函数；K(Z,z_t+1)为历史状态动作对与新输入的状态动作对z_t+1之间的协方差矩阵；

根据状态动作对z_t+1＝<s_t+1,a_t+1>以及对应的Q值Q(z_t+1)更新高斯预测模型；

(26)更新当前状态：s_t＝s_t+1，当s_t为终止状态且满足收敛条件时，强化学习结束，得到最优策略；否则转步骤(23)。

具体地，高斯预测模型中的核函数k(·)为高斯核函数：

其中σ_k为高斯核函数的宽度。

具体地，步骤(26)中所述的收敛条件为：Q值的变化小于Q值门限Q_th，即：|Q(z_t)-Q(z_t+1)|<Q_th。

有益效果：与现有技术相比，本发明公开的服务组合方法具有以下优点：在本发明中，进行强化学习Q值计算时，改进了原来通过值表对Q值进行记录和查找的传统做法，将每次选择调用的服务和观测到的QoS属性视为一个未知函数的输入输出，在Q值的迭代过程中，通过高斯过程估计Q值，而非通过值表进行查找，同时也对高斯过程的参数进行学习和更新，继而使得对Q值的预测更为精确，使得最终得到更优的服务组合结果。同时，采用了高斯过程的强化学习服务组合方法，能够从已有数据中训练出一个高斯过程模型，从而能对新的数据进行预测和估计，具有良好的泛化能力，更能适应动态、多变的web服务组合环境。

附图说明

图1是基本的服务组合模型；

图2是以MDP建模的服务组合示意图；

图3是基本的高斯过程示意图；

图4是结合高斯过程和强化学习的服务组合方法流程图。

具体实施方式

下面结合附图和具体实施方式，进一步阐明本发明。

服务组合的基本模型如图1所示，一个复杂软件系统可以视作由多个组件或子系统组成的工作流程，在服务组合领域中，组件即web服务。因此在进行服务组合时，用户的需求可以用一个抽象任务工作流图建模，其中各个组件即抽象服务。对于每个抽象服务，可能存在多个候选服务，这些服务具有类似的功能，但是有不同的QoS(服务质量)，所以可以基于QoS属性从候选服务中选择合适的具体服务，最终组合出可用的服务组合系统。

本发明公开的结合高斯过程与强化学习的服务组合方法，包括如下步骤：

步骤1、将服务组合问题建模为一个四元组马尔可夫决策过程：

M＝<S,A,P,R>

其中S是环境中有限状态的集合；A是可调用的动作的集合，A(s)表示在状态s下可进行的动作的集合；P是描述MDP状态转移的函数，P(s′|s,a)表示在状态s下调用动作a后转移到状态s′的概率；R是回报值函数，R(s,a)表示在状态s下调用动作a所得的回报值。

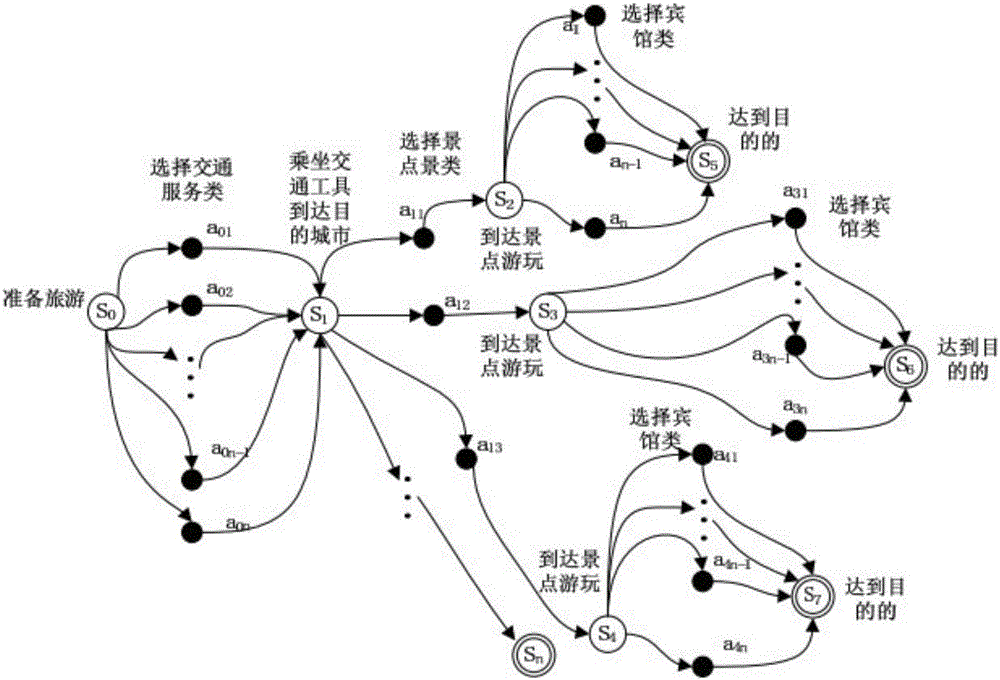
图2给出了由MDP建模的服务组合的一个示例，该示例描述了一个旅游出行时的服务组合过程。MDP模型中，可以调用的候选服务建模为不同的动作。调用不同的动作，可能到达不同的状态，同时新的状态决定了接下来可以调用的服务的集合。对于调用的不同的服务，通过观测到的QoS属性来评估服务的质量，即MDP模型中的回报函数。这样，一个服务组合问题便转化为了一个MDP模型，从而可以通过强化学习方法进行求解优化。

步骤2、应用基于Q-learning的强化学习方法求解四元组马尔可夫决策过程，得到最优策略；

MDP模型的求解即找到每个状态下的最佳服务选择策略，使得最终组合的结果更优。在MDP模型中，选择一个动作的优劣不仅仅取决于该动作所产生的立即回报值，同时也和该动作导致的后续状态和回报有关，在强化学习算法Q-learning中，用Q值函数Q(s,a)评估在状态s下选择动作a的估计价值，其迭代公式如下：

其中σ为学习率，用来控制每次更新Q值时改变的程度大小；γ为折扣率，用来控制未来状态的影响程度；强化学习理论认为立即回报值的影响应大于未来的可能回报值，因此γ的值为0到1之间。r即为R(s,a)，为在状态s下执行动作a的回报值。Q(s′，a′)代表在执行动作a后，转移到状态s′后选择a′的Q值，用来表示未来的奖励值。

传统强化学习过程中，对计算的Q值进行记录，在之后更新Q时，Q(s′，a′)通过之前计算、记录的Q值表中查找得到，在某些应用场景中已经足够。但是在高度动态的服务组合场景中，这种方法缺乏泛化能力，不能应对真实场景中的数据变化。并且随着服务组合规模的扩大，值表存储和查询所需的空间和时间也会消耗很大的计算能力，对于实时性的要求也无法很好的满足。因此本发明提出通过高斯过程对Q值的估计进行建模，从而提高泛化能力，更好的应对动态环境，在实际应用中得到更好的效果。

如图4所示，具体包括如下步骤：

(21)将状态动作对z＝<s,a>作为输入，对应的Q值Q(z)作为输出，建立Q值高斯预测模型；

高斯过程的示意如图3，根据已知的输入输出数据，训练出一个高斯过程模型，当新的输入到来时，通过模型预测出其对应的输出。高斯过程模型由均值函数和协方差函数唯一确定，容易进行调整和优化，迭代收敛也相对较快。

具体的，选取一组n个训练样本{(z_i＝(s_i,a_i),Q(z_i))|i＝1..n}，其中z_i＝(s_i,a_i)为状态动作对，为输入；Q(z_i)为状态动作对对应的Q值，为输出。z^*和Q^*为需要预测的数据。高斯过程认为输入与输出满足一个联合概率分布，用K(X,X^*)表示n×n^*的所有训练点X与测试点X^*的协方差矩阵(n为训练点个数，n^*为测试点个数)，K(X,X^*)矩阵的第i行j列元素为k(X_i,X^*)，X_i为集合X的第i个元素。

K(X,X),K(X^*,X),K(X^*,X^*)与此类似，则输出训练点与输出测试点的联合分布为：

计算可得Q(z^*)的均值的期望为α_*^TK(Z,Z^*)。其中其中ω_n代表不确定性参数，本实施例中取值为1；I为单位矩阵；Z为历史状态动作对的集合，f为与Z对应的历史Q值的集合，K(Z,Z)为历史状态动作对之间的协方差矩阵，其第i行j列元素为k(z_i,z_j)，k(·)为核函数；K(Z,z_t+1)为历史状态动作对与新输入的状态动作对z_t+1之间的协方差矩阵；

(22)初始化Q-learning中学习率σ，折扣率γ，贪心策略概率ε，当前状态s＝0，当前时间步长t＝0；

(23)用概率为ε的贪心策略选择一个服务a作为当前服务a_t并执行，具体为：在(0,1)区间随机产生一个随机数υ，如果υ>ε，随机选择一个新的服务a；如果υ≤ε，选择使当前Q值最大的服务作为新的服务a；这样可以避免陷入局部最优；

(24)记录在当前状态s_t下执行当前服务a_t的回报值r_t和执行服务a后的状态s_t+1；根据下式计算在状态动作对z_t＝<s_t,a_t>下的Q值：

其中Q(z_t)为在状态动作对z_t＝<s_t,a_t>下的Q值，σ为学习率，r为回报值，γ为折扣率，s_t+1为执行服务a_t后从当前状态s_t转移到的后继状态，a_t+1为在状态s_t+1下选择的服务，Q(s_t+1,a_t+1)表示在状态动作对<s_t+1,a_t+1>下的Q值；

(25)按照高斯预测模型更新Q值：

其中I为单位矩阵，ω_n为不确定性参数，Z为历史状态动作对的集合，为与Z对应的历史Q值的集合，K(Z,Z)为历史状态动作对之间的协方差矩阵，其第i行j列元素为k(z_i,z_j)，k(·)为核函数；K(Z,z_t+1)为历史状态动作对与新输入的状态动作对z_t+1之间的协方差矩阵。核函数有多种可以使用，本实施例中核函数K选用高斯核函数：

其中σ_k为高斯核函数的宽度。

由于新加入的数据点，高斯模型已经产生了变化，所以需要根据状态动作对z_t+1＝<s_t+1,a_t+1>以及对应的Q值Q(z_t+1)更新高斯预测模型，用于下一次Q值的迭代更新；

(26)更新当前状态：s_t＝s_t+1，当s_t为终止状态且满足收敛条件时，强化学习结束，得到最优策略；否则转步骤(23)。

本实施例中的收敛条件是Q值变化稳定，即Q值的变化小于Q值门限Q_th，即：|Q(z_t)-Q(z_t+1)|<Q_th，此时得到最优策略，根据此最优策略获取最终的服务组合结果。