一种基于主成分序列的空频编码盲识别方法与流程

本发明涉及一种空频编码盲识别方法，具体涉及一种对多输入多输出正交频分复用(multipleinputmultipleoutput-orthogonalfrequencydivisionmultiplexing，mimo-ofdm)系统使用的空频编码进行盲识别的方法，可适用于多径衰落环境较低信噪比下，软件定义无线电、认知无线电及通信对抗、通信物理层安全，属于无线通信信号处理技术领域。

背景技术：

多输入多输出正交频分复用(mimo-ofdm)系统是新一代无线通信的关键技术，它能够在有效获得空间分集的同时对抗多径衰落，被广泛应用于第四代蜂窝移动通信(4thgeneration-longtermevolution,4g-lte)中。由于实际4g-lte技术协议中定义的ofdm符号数为奇数，所以必须使用空频编码对数据进行传输。对空频编码进行有效盲识别，可以为软件定义无线电设备、认知无线电设备提供可靠的通信参数，也可以根据空频编码构造相应的干扰样式对窃听设备进行干扰保障通信安全。因此对空频编码盲识别的方法进行研究具有重要的理论意义和应用价值。

空频编码盲识别是指在发送端有效信息未知的情况下，仅通过接收信号的特征识别发送端的空频编码的编码方式。空频编码的盲识别是一个新兴的课题，目前空频编码方式盲识别可通过扩展空时分组码识别算法来进行。然而这些算法不能有效适应多径环境，在频率选择性信道下识别效果较差。

文献[v.choqueuse,m.marazinetal.,blindrecognitionoflinearspacetimeblockcodes:alikelihoodbasedapproach.ieeetrans.signalprocessing,58(3),2010,1290-1299]中引入模式选择方法用于识别平坦信道环境下的空时编码，将其扩展到频域进行空频编码的识别。该方法为基于信息论准则的设计思想，对频域接收信号的协方差矩阵进行特征值分解，将得到的特征值和待估识别参数带入到模式选择的似然函数中，计算使似然函数最大的参数值，进而可确定发射端使用的空频编码模式。但是该方法存在的不足是：一方面，不能识别速率相同的码型；另一方面，此方法的识别性能在多径环境下随信噪比增高出现下降；因此该方法无法满足空频编码盲识别的工程要求。

文献[eldemerdashya,dobreoa,mareym,etal.anefficientalgorithmforspace-timeblockcodeclassification.globalcommunicationsconference(globecom),2013:3329-3334]中利用四阶统计量识别平坦信道环境下的空时编码，将其扩展为频域中空频编码的识别，其设计思想基于不同编码的四阶延迟积在给定延迟下出现不同的峰值，通过判断两个峰值之间的距离来区分不同的空频编码。但是该方法也存在不足：一方面，不能识别速率相同的码型；另一方面此方法受制于多径环境以及采样样本数。由此可见，该方法也无法满足空频编码盲识别的工程需求。

中国专利cn104038317a(公开日：2014-09-10)(下文成为专利[1])公开了一种基于特征提取和分集技术的空频码模式盲识别方法，该方法的思路是：首先，对频域接收信号的自相关矩阵进行特征值分解，然后利用分集技术迭代特征值，增大信号特征值和噪声特征值之间的差距，最后通过比值判决法得到发送空频码的估计符号数向量，与候选集中码型的理论符号数向量求欧几里得距离差，得出最终的识别码型。该方法存在的不足是：一方面，仅对比了特征值大小，在噪声功率较大时，特征值比值差异不明显，因而无法在较低信噪比的情况下精确地描述噪声特征值的数学特征；另一方面，该法在估计距离判决和时，使用了欧几里得距离，在低信噪比时，低估的概率远大于高估的概率；因而在低信噪比的条件下性能较差，无法满足空频编码盲识别的工程要求。

技术实现要素：

针对现有技术的不足，本发明旨在提供一种基于主成分序列的空频编码盲识别方法，通过对接收信号的自相关矩阵进行特征提取，并利用精确的tracy-widom分布提高空频编码在小样本、低信噪比下的盲识别性能，以满足空频编码盲识别的工程要求。

为了实现上述目的，本发明采用如下技术方案：

一种基于主成分序列的空频编码盲识别方法，包括如下步骤：

s1对接收天线数据进行预处理，构造相邻子载波符号矩阵；

s2计算相邻子载波符号矩阵的自相关矩阵，并进行特征值分解，得到特征值向量，以及对应的特征值集合；

s3通过基于噪声功率迭代的串行假设检验判断主成分个数；

s4构造估计相邻载波主成分序列向量；

s5比较估计相邻载波主成分序列向量与空频编码集合主成分序列的距离判决和，选择距离判决和最小的编码作为识别的结果。

需要说明的是，步骤s1具体为：

1.1)接收端通过nr根接收天线接收到已经经过载波解调长度为σ的信号序列，得到nr×σ的接收信号矩阵xr；

1.2)去除接收信号矩阵xr中的循环前缀，对其进行ofdm解调后，得到nr×(m×l)维解调信号矩阵x，其中，x(m,l)为解调后第m个ofdm符号中第l个子载波上的接收信号向量，1≤m≤m，1≤l≤l，m为接收到的ofdm符号数，l为每个ofdm符号中的子载波个数；

1.3)取解调信号矩阵x第v个子载波及其相邻的子载波上的侦听信号，将两个子载波上的信号向量化，构成2nr×m维相邻子载波符号矩阵yv：

其中，1≤v≤l。

需要说明的是，步骤s2具体为：

2.1)将步骤s1得到的相邻子载波符号矩阵yv的实部和虚部并联，得相邻载波并联矩阵

其中，表示取实部运算，表示取虚部运算；

2.2)计算相邻载波并联矩阵的自相关矩阵：其中，e[·]表示求期望运算，[·]^t表示求转置运算；

2.3)对相邻载波并联矩阵的自相关矩阵rv做特征值分解，将得到的特征值按降序排列，构成特征值向量：

其中，为第v个子载波及其相邻载波自相关矩阵rv的第k个特征值，nr为接收天线的数量；

则特征值集合为

需要说明的是，步骤s3具体如下：

3.1)对于第v个子载波及其相邻子载波，根据步骤s2得到的特征值集合和终止条件利用迭代算法计算噪声功率的估计值集合

3.2)取第v个子载波及其相邻子载波的第k个噪声功率估计值对特征值进行归一化处理得到相对应的随机变量：

将此随机变量作为检验统计量；

3.3)求解判决门限值γk：

其中，表示第一类tracy-widom分布的逆累积分布函数，pfa表示预先设定的虚警概率；

3.4)确定主成分个数：

从k＝1开始搜索，当第一次检测出时，输出主成分个数

需要说明的是，步骤s4具体为：计算相邻子载波符号矩阵y1,…,yn-8的主成分个数n＝l，l为每个ofdm符号中的子载波个数，构造估计相邻载波主成分序列向量

需要说明的是，步骤s5具体为：

5.1)利用步骤s4得到的估计相邻载波主成分序列向量计算空频码组成码型集合ω中所有码型的主成分序列与估计相邻载波主成分序列向量的距离判决和：

其中|·|表示取绝对值，ε(·)表示阶跃函数，有：而表示向上取整，表示空频码集合ω中的第t种码型的第v个子载波及其相邻子载波的主成分序列值，t为空频码集合ω中的码型个数；n＝l，l为每个ofdm符号中的子载波个数；

5.2)空频码组成码型集合ω中所有码型的主成分序列与估计相邻载波主成分序列向量的距离判决和构成距离判决和向量π＝[d1,d2...dt]，取向量π中最小的dt所对应的码型作为判决结果。

进一步需要说明的是，在步骤1.2)中，所述ofdm解调采用的是n点的fft变换，其中n＝l。

进一步需要说明的是，步骤2.3)中，对自相关矩阵rv进行特征分解采用的是正交对角分解法，具体为：

2.3.1)在自相关矩阵rv两边分别乘以正交矩阵p及其转置矩阵p^t，得到特征值对角矩阵prvp^t；

2.3.2)从特征值对角矩阵prvp^t中提取协方差矩阵rv的特征值。

进一步需要说明的是，步骤3.1)中，计算噪声功率的估计值集合具体如下：

3.1.1)根据特征值将噪声功率的估计值初始化为噪声方差的最大似然估计值

3.1.2)根据噪声方差的最大似然估计值和特征值计算中间变量ηj：

其中，j＝1,2,...,k，将中间变量ηj带入迭代公式求出新的噪声方差估计值具体迭代公式由下列公式确定：

3.1.3)设置一个与的最大差值γ，令其值为10^-5，将与进行比较：

若比较差值的结果大于γ，则令重复3.1.2)；

若比较差值结果小于或等于γ，则终止迭代过程，就是噪声功率的估计值

本发明的有益效果在于：

第一、由于本发明采用了基于精确tracy-widom分布的主成分序列法，提高了识别的收敛速度，对噪声特征值的数学特征描述更加精确，从而能够在小样本数据条件下取得良好的识别效果，提高了估计的实时性，满足了空频码盲识别的工程需要。

第二、由于本发明中噪声功率采用迭代方法，使得检验统计量的构造在在较少的天线数时也较为精确，可在满足一定识别性能的条件下降低接收机体积和成本。

第三、由于本发明中检验统计量设计使用了全部的子载波，使得ofdm符号中每一个子载波的信息都得到了有效利用，从而在较低信噪比情况下也可以得到较好的识别性能。

第四、由于本发明中计算判决距离和的方法引入过高估计次数这一因素，从而降低了在低信噪比情况下的过低估计的可能性，从而在较低信噪比情况下也可以得到较好的识别性能。

附图说明

图1是本发明使用的系统框图；

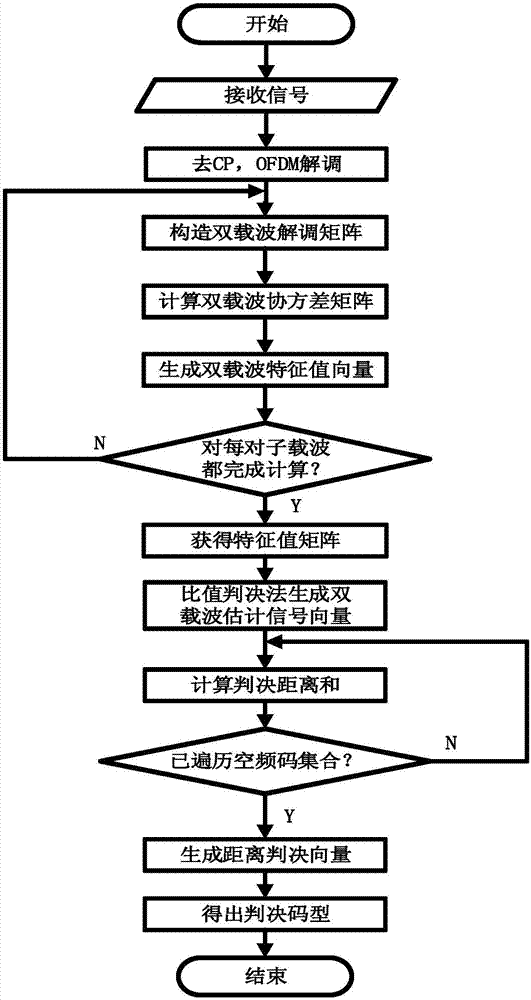
图2是本发明的实现流程图；

图3是不同信噪比和接收ofdm符号数条件下本发明及专利cn104038317a的技术的平均识别正确率对比示意图；

图4是不同信噪比和接收天线数条件下本发明及专利[1]对于上文提到的空频码组成码型集合ω的全部码型的平均识别正确率对比示意图。

具体实施方式

以下将结合附图对本发明作进一步的描述，需要说明的是，本实施例以本技术方案为前提，给出了详细的实施方式和具体的操作过程，但本发明的保护范围并不限于本实施例。

实现本发明目的的技术思路是：首先，对频域接收信号的自相关矩阵进行特征值分解，然后利用基于噪声功率迭代的串行假设检验判断接收信号码元主成分个数，与空时编码集合ω中码型的理论码元主成分求距离判决和，得出最终的识别码型。该识别方法使用的系统模型包括一台发射机、一台盲接收机，其中，发射机的天线数目为nt，接收机的天线数目为nr，nr＞nt，发送信号采用ofdm调制方式并使用空频编码。空频编码集合在表1中列出：

表1

其中，sa(singleantenna)表示单天线，sm(spatialmultiplexing)表示空间多路复用，ostbc(orthogonalspacetimeblockcode)表示正交空时分组编码。每一个ofdm符号的子载波数为n。

参照图1，本发明使用的系统包括：nt根发射天线，nr根接收天线，调制方式为4-qam(quadratureamplitudemodulation)。在发射端，调制后串行发送序列经空频编码后转换为并行发送序列，再将并行序列进行ofdm调制后发送出去。在接收端，通过nr根接收天线得到接收信号矩阵为xr，其中，nr＞nt。图1就是一种多输入多输出的正交频分复用系统。

本发明就是根据接收信号矩阵xr，盲识别出发送端使用的空频编码模式。

参照图2，本发明的具体实现步骤如下：

步骤1、对接收天线数据进行预处理，构造相邻子载波符号矩阵：

(a1)接收端通过nr根接收天线接收到已经经过载波解调长度为σ的信号序列，得到nr×σ的接收信号矩阵xr；

(a2)去除接收信号矩阵中的循环前缀，对其进行ofdm解调后，得到nr×(m×l)维解调信号矩阵x，其中，x(m,l)为解调后第m个ofdm符号中第l个子载波上的接收信号向量，1≤m≤m，1≤l≤l，m为接收到的ofdm符号数，l为每个ofdm符号中的子载波个数；

(a3)取相解调矩阵x第v个子载波及其相邻的子载波上的侦听信号，将两个子载波上的信号向量化，构成2nr×m维相邻载波解调矩阵yv：

其中，1≤v≤l；

步骤2、计算相邻子载波符号矩阵的自相关矩阵，并进行特征值分解：

(b1)将相邻子载波符号矩阵yv的实部和虚部并联，得相邻载波并联矩阵

其中，表示取实部运算，表示取虚部运算；

(b2)计算相邻载波并联矩阵的自相关矩阵：其中，e[·]表示求期望运算，[·]^t表示求转置运算；

(b3)对相邻载波并联矩阵的自相关矩阵rv利用正交对角分解法做特征值分解，将得到的特征值按降序排列，构成特征值向量其中，ρ^(v)为相邻载波自相关矩阵rv的特征值，

步骤3、通过基于噪声功率迭代的串行假设检验判断主成分个数：

(c1)对于第v个子载波及其相邻子载波，进行噪声功率估计：

①根据特征值将噪声方差估计值初始化为噪声方差的最大似然估计值

②根据噪声方差的最大似然估计值和特征值计算中间变量ηj：

其中，j＝1,2,...,k，将中间变量ηj带入迭代公式求出新的噪声方差估计值具体迭代公式由下列公式确定：

③设置一个与的最大差值γ，令其值为10^-5，将与进行比较：

若比较差值的结果大于γ，则令重复②；

若比较结果满足终止迭代条件，则终止迭代过程，就是噪声方差估计值

(c2)构造检验统计量

(c3)求解判决门限值γk：

其中，表示第一类tracy-widom分布的逆累积分布函数，pfa表示预先设定的虚警概率，

(c4)确定主成分个数：

从k＝1开始搜索，当第一次检测出时，输出主成分个数

步骤4、构造估计主成分序列：

重复s1的(a3)、s2、s3计算y1,…,yn-8的主成分个数构造相邻载波主成分序列向量

步骤5、比较估计主成分序列与空频编码集合主成分序列的距离判决和，选择距离判决和最小的编码作为识别的结果：

(d1)利用步骤4中的双载波估计向量计算距离判决和：

其中|·|表示取绝对值，ε(·)表示阶跃函数，有：而表示向上取整；t为空频码集合ω中的码型个数，表示空频码集合ω中的第t种码型的第v个子载波及其相邻子载波的的主成分序列值；

(d2)重复步骤(d1)，计算码型集合ω中每种空频码对应的距离判决和，构成距离判决和向量π＝[d1,d2...dt]，取向量π中最小的dt所对应的码型作为判决结果。

所述步骤s5中的空频编码集合为空时分组码在ofdm系统中应用时，利用频域传输的别称，两者具有相同的编码矩阵，其中编码矩阵可参考文献[alamoutism.asimpletransmitdiversitytechniqueforwirelesscommunications.selectedareasincommunications,ieeejournalon,1998,16(8):1451-1458.]和文献[tarokhv,jafarkhanih,calderbankar.space-timeblockcodesfromorthogonaldesigns.informationtheory,ieeetransactionson,1999,45(5):1456-1467.]。表2为空频编码集合ω中各空频编码的主成分序列。

表2

本发明的效果可通过以下仿真进一步详细说明。

仿真1：在不同的信噪比及接收ofdm符号数的条件下，用本发明及专利[1]对空频码集合ω进行识别。

设仿真信噪比的范围为-12-8db，间隔为2db，接收天线为8，接收ofdm符号数集合为{50，100，200，400}，ofdm子载波为64个，调制方式为4-qam，多径数为4，虚警概率设为10^-4。空频码集合ω中每个码型在每个信噪比点上进行1000次蒙特卡洛实验，记录下每个信噪比下不同码型的的正确识别次数，通过除以总的实验次数得到每个信噪比条件下的识别正确率，全部码型的平均识别率仿真结果如图3。从图3可以看出：随着信噪比的上升，本发明及专利[1]的正确识别率均得到了提高；而在同一信噪比条件下，接收的ofdm符号越多，本发明的正确识别率越高，这是由于随着接收ofdm符号数的上升，检验统计量的数学特性就更加精确，正确识别率就随之上升。另外，对比本发明与专利[1]，可以发现，在相同的信噪比及ofdm符号数条件下，本发明的性能优于专利[1]的性能。例如当接收ofdm符号数为50个，相同条件下本发明较之前的方法性能大约提升4db，而当接收ofdm符号数为400个，相同条件下，性能提升6db。这是由于专利[1]的方法仅对比了特征值大小，尤其是在噪声功率较大时，特征值比值差异不明显，本发明利用噪声特征值服从第一类tracy-widom分布的特性，使其在较低信噪比也能够较为精确的描述噪声特征值的数学特征。因此本发明较专利[1]的方法有性能上的提升。

仿真2：在不同的信噪比及接收天线的条件下，用本发明及专利[1]对空频码集合ω进行识别。

设仿真信噪比为-8-10db，间隔为2db，接收天线数的集合为{4,6,8}(因为空频码集合ω中的所有码型的最大发射天线数目ntmax＝3，而本发明要求接收天线数nr＞nt，所以接收天线的数最小为4)，接收ofdm符号数为100，ofdm子载波为64个，调制方式为4-qam，多径数为4，给定的虚警概率为10^-4。空频码集合ω中每个码型在不同的接收天线数条件下进行1000次蒙特卡洛实验，记录下不同的接收天线数下不同码型的正确识别次数，通过除以总的实验次数得到每个接收天线数下的识别正确率，全部码型的平均识别率仿真结果如图4，从图4可以看出，在相同条件下，随着接收信噪比的增加，本发明的正确识别率有所上升；另外，在相同条件下，随着接收天线数的增加，本发明的正确识别率也得到了增加。对比图中对于专利[1]的仿真结果可以发现，在相同条件下，本发明的性能要优于专利[1]中方法的性能。例如在接收天线数为8，在相同的条件下，本发明的性能较专利[1]中方法提升了5db；而在信噪比为0db时，本发明在接收天线数为8时，正确识别率已接近1，而专利[1]的方法正确识别率仅0.35左右。这是由于本发明利用噪声特征值服从第一类tracy-widom分布的特点，在较低信噪比情况下，更为精确地描述了噪声特征值的数学特征，从而能更准确的区分信号特征值和噪声特征值；而专利[1]仅对比了特征值的大小，在低信噪比条件下，对噪声特征值的数学特征描述不够精确，从而导致性能的下降；另外，专利[1]在计算距离判决和时，简单的采用了欧几里得距离，忽略了采用基于随机矩阵论的串行假设检验在低信噪比下低估的概率远大于高估的概率这一事实，从而造成了低信噪比条件下性能的不足。而本发明对于距离判决和的计算，引入了过高估计次数这一因素，从而能更加合理的给出结果，提升了性能。

对于本领域的技术人员来说，可以根据以上的技术方案和构思，作出各种相应的改变和变形，而所有的这些改变和变形都应该包括在本发明权利要求的保护范围之内。