一种基于SM2算法的无证书安全签名方法与流程

本发明属于公钥密码领域，特别涉及基于国密sm2算法的无证书认证系统的安全签名方法。

背景技术：

公钥密码技术在计算机技术和网络技术高度发展的今天，已得到了广泛应用。数字签名技术和公钥加密技术已深入到人们的日常生活。为了保证数字签名的唯一性和签名私钥的安全性，通常由私钥所有者将签名私钥保存在密码设备内，签名运算也在密码设备内执行。所采用的密码设备在服务器端通常为密码机，在客户端为带cpu的usbkey和ic卡等。在云计算环境和手机移动终端等环境下，使用这些密码设备来保存密钥和执行密码运算就很不方便，因而出现了将密钥保存在手机文件中并在手机上执行密码运算的应用需求。这种软环境给密钥的存储安全和使用安全带来很大隐患。为了提高密钥存储和密码运算的安全性，可以采用密钥共享的方式，由多个用户联合对同一消息签名，最后形成的签名可使用共享的公钥进行验证。对于国密sm2签名算法，由于其算法的特殊性，实现密钥共享和联合签名比较困难。此外，对于一种无双性对运算的无证书公钥密码体制(参见申请号为201410772127.5的专利)，由多方联合完成基于sm2算法的签名则更加困难，目前尚未发现解决这种应用需求的方法。

技术实现要素：

本发明针对无双性对运算的无证书公钥密码体制，提出一种用户密钥共享方法，在无证书密钥生成中心的协助下，n(n≥2)个用户分别生成不同的私钥，并生成一个共享公钥。在需要对消息作数字签名时，由多方联合完成对消息的sm2签名，签名依赖方可用共享公钥按sm2验证签名算法进行验证。这种密钥共享和签名方法满足以下要求：

(1)n个用户对各自的私钥具有完全自主权，其他用户或任何第三方(包括无证书密钥生成中心)对该私钥都不可知。

(2)多方合作完成的数字签名符合国密sm2签名标准要求，签名依赖方可使用共享公钥进行验证。

(3)少于n个用户合作不能构造完整合法的sm2签名。

本发明所涉及到的椭圆曲线参数按国密sm2算法标准设置。有限域上的椭圆曲线记为e(fq)，其基点为g，而g的阶为素数n。

本发明中，无证书密钥生成中心称为kgc，n个用户分别记为u1,u2,…,un，他们共享一个标识id，h(x)为sm3杂凑函数。

一、密钥生成

本发明所述生成无证书共享密钥的方法涉及kgc和用户u1,u2,…,un，具体技术方案描述如下。

g01所述kgc设置系统私钥sm和系统公钥ppub，完成系统建立。

g02所述用户u1随机选取k1∈[1,n-1]，计算p1＝k1g，发送p1到用户u2。

g03对于i＝2,3,…,n-1，所述用户ui在收到pi-1后随机选取di,ki∈[1,n-1]，计算pi＝(di)^-1pi-1+kig，发送pi到ui+1。

g04所述用户un在收到pn-1后随机选取dn,kn∈[1,n-1]，计算pn＝(dn)^-1pn-1+kng，发送pn到kgc。

g05所述kgc随机选取k0∈[1,n-1]，计算p＝pn+k0g，s0＝k0+h(id||p)sm(modn)，kgc将p作为用户实体的部分公钥发布，发送s0到用户un。

g06所述用户un计算sn＝dn(kn+s0+1)(modn)，qn＝(dn)^-1g，发送sn和qn到用户un-1。并将dn作为用户un的私钥保存，将qn作为用户un的公钥参数保存。

g07对于i＝n-1,n-2,…,2，所述用户ui计算si＝di(ki+si+1)(modn)，qi＝(di)^-1qi+1，发送si和qi到ui-1。并将di作为用户ui的私钥保存，将qi作为用户ui的公钥参数保存。

g08所述用户u1计算d1＝(k1+s2)^-1(modn)，q1＝(d1)^-1q2，将d1作为用户u1的私钥保存，将q1作为用户u1的公钥参数保存。

按此过程生成的用户密钥信息汇总如下：

(1)用户ui的私钥为di(i＝1,2,…,n)。

(2)用户ui的公钥参数为qi＝(di…dn)^-1g(i＝1,2,…,n)。

(3)n个用户的共享公钥为q＝((d1d2…dn)^-1–1)g。

(4)n个用户的共同私钥为d＝(d1d2…dn)^-1–1(modn)。

(5)n个用户的共同部分公钥为p。

在密钥生成的所有环节中，共同私钥d并不实际出现，任何人都可以通过公式q＝p+h(id||p)ppub计算得到共享公钥。

二、签名与验签

本发明所述安全签名方法是指用户实体需要对消息作数字签名时，由n个用户联合按序完成对消息的签名，且签名结果为普通的sm2签名，签名接收方可以使用共享公钥进行验证。

所述安全签名方法涉及到的n个用户为u1,u2,…,un。用户ui具有私钥di和公钥参数qi，他们的共享公钥为q＝((d1d2…dn)^-1–1)g，且有q1＝(d1d2…dn)^-1g，q2＝(d2…dn)^-1g，…，qn＝(dn^-1)g。

设待签名的消息为m，e＝h(z||m)是对消息m的摘要值。由n个用户按次序联合完成对摘要值e的sm2签名。所述多方联合签名的方案如下。

s01所述用户u1计算摘要值e，再随机选取k1∈[1,n-1]，计算r1＝k1q1，发送e和r1到用户u2。

s02对于i＝2,3,…，n-1，所述用户ui在收到ri-1后随机选取ki∈[1,n-1]，计算ri＝ri-1+kiqi，发送e和ri到用户ui+1。

s03所述用户un在收到rn-1后随机选取kn∈[1,n-1]，计算rn＝rn-1+knqn。

s04设rn＝(x1,y1)，所述用户un计算r＝(e+x1)(modn)，sn＝kn+rdn(modn)，生成部分签名(r,sn)，发送部分签名(r,sn)到用户un-1。

s05对于i＝n-1,n-2,…,1，所述用户ui在收到用户ui+1的部分签名(r,si+1)后，首先验证该部分签名。验证过程为：计算qi+1＝diqi，ri+si+1qi+1–rg＝(x1’,y1’)，检验r＝(e+x1’)(modn)是否成立。若验证通过，再计算si＝ki+si+1di(modn)，生成部分签名(r,si)，当i>1时，用户ui发送部分签名(r,si)到用户ui-1。

s06所述用户u1计算s＝s1–r(modn)，生成最终签名(r,s)。

按此步骤生成的签名(r,s)可以使用共享公钥q按sm2签名的验证算法进行验证。

签名接收者在接收到消息m和签名(r,s)后，首先根据用户id及部分公钥p计算共享公钥q，再按sm2签名验证算法，令u＝r+s(modn)，计算摘要值e＝h(z||m)，sg+uq＝(x1’,y1’)，最后验证r＝(e+x1’)(modn)是否成立。

通过下面三个步骤，可以证明本发明所述的多方联合签名方法生成的签名能够通过sm2签名验证算法的验证。首先证明对于i＝n-1,n-2,…,1，步骤s05中对部分签名(r,si+1)的验证是正确的，然后证明最终签名能够使用共享公钥q进行验证。

v01验证部分签名(r,sn)。

由于sn＝kn+rdn(modn)，qn＝(dn)^-1g，所以(x1’,y1’)＝rn-1+snqn–rg＝rn-1+knqn+rg–rg＝rn-1+knqn＝rn＝(x1,y1)，因此有x1’＝x1，所以r＝(e+x1’)(modn)成立。

v02对于i＝n-1,n-2,…,2，假定已经验证了部分签名(r,si+1)，即已经有ri+si+1qi+1–rg＝rn成立，来验证部分签名(r,si)，即验证ri-1+siqi–rg＝rn成立。

由于qi＝(di)^-1qi+1，ri-1＝ri–kiqi，si＝ki+si+1di(modn)，

所以ri-1+siqi–rg＝(ri–kiqi)+(kiqi+si+1di(di)^-1qi+1)–rg＝ri+si+1qi+1–rg＝rn。

于是部分签名(r,si)得到验证。

v03验证最终签名(r,s)。

按sm2签名验证算法，只需要验证sg+uq＝rn成立，其中q为用户实体的实际公钥。

在验证过程v02中，已经验证了r1+s2q2–rg＝rn成立。由于s＝s1–r(modn)，所以u＝r+s＝s1(modn)，又因为s1＝k1+s2d1(modn)，r1＝k1q1，q1＝(d1)^-1q2，q＝q1–g，所以

sg+uq＝(s1–r)g+s1(q1–g)

＝s1q1–rg＝(k1+s2d1)q1–rg

＝k1q1+s2d1(d1)^-1q2–rg

＝r1+s2q2–rg＝rn

至此，所述最终签名(r,s)得到完全验证，因此(r,s)就是一个标准的sm2签名。

本发明所述安全签名方法，共享公钥的n个用户都不能获取其他用户私钥的信息，少于n个用户联合不能构造对消息的合法数字签名，必须由n个用户联合才能完成签名。本发明所述签名过程简单，签名过程中，每个用户只需要各做一次多倍点运算，运算效率高，签名结果符合国密sm2签名算法标准。

从前面的签名过程和验证签名的过程可见，本发明所述安全签名方法，不仅适应于基于sm2的无证书公钥密码体制，而且可以适用于任何使用sm2算法的系统，只要n个用户分别持有的私钥d1,d2,…,dn与共享公钥q之间满足q＝((d1d2…dn)^-1–1)g，这n个用户就可以按上述签名过程联合完成对一个消息的sm2签名。

本发明所述由n个用户联合完成签名的方法，签名过程是按次序完成的，但这个次序是可以调整的。如果需要调整签名次序，只需要按新的签名次序重新生成公钥序列q1,q2,…,qn即可。例如，将签名次序调整为ui1,ui2,…,uin后，n个用户重新依次计算qin＝(din)^-1g,qi(n-1)＝(di(n-1))^-1qin,…,q1＝(d1)-1q2，则可按新的次序来完成联合签名。

附图说明

图1为本发明所述无证书共享密钥生成流程。

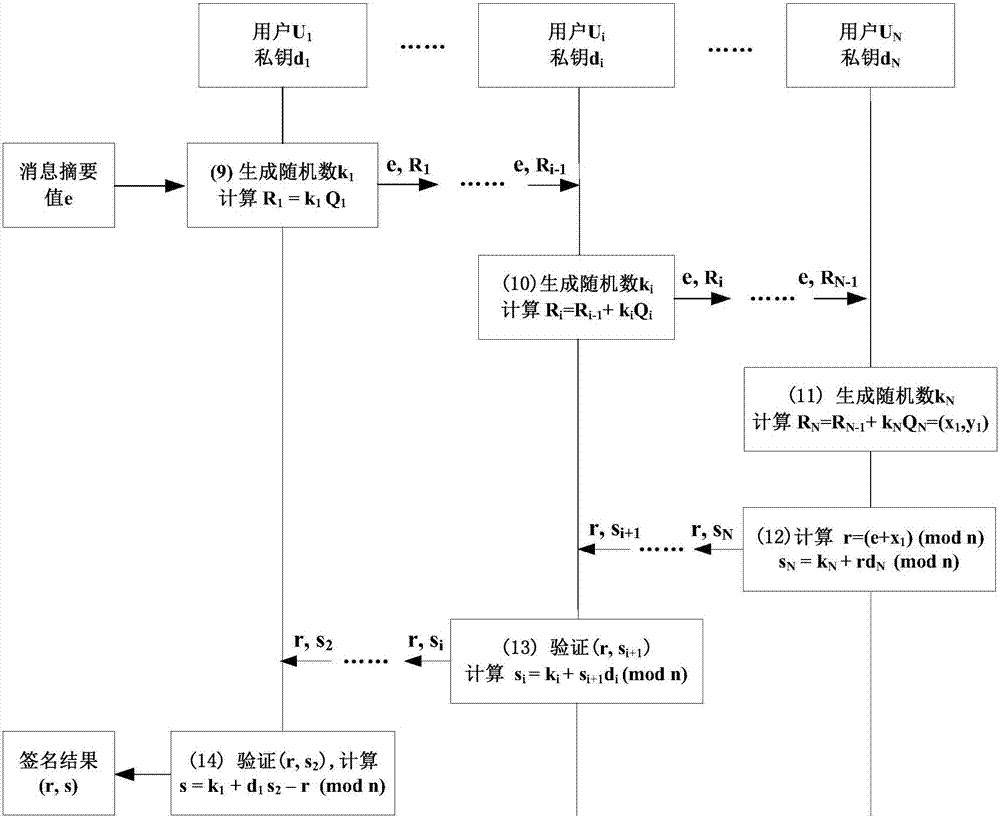
图2为本发明所述多方联合安全签名流程。

具体实施方式

本发明针对基于sm2算法无证书公钥密码体制提出了一种安全的签名方案，下面根据附图详细说明本发明的实施方式。

图1所示为基于无证书公钥密码体制的密钥生成实施流程。本发明所涉及到的有限域上的椭圆曲线参数按国密sm2算法标准设置，所使用的有限域上椭圆曲线记为e(fq)，其基点为g，而g的阶为素数n，h(x)为sm3杂凑函数。

无证书密钥生成中心称为kgc，共享密钥的n个用户分别记为u1,u2,…,un，他们共享一个用户标识id。

步骤(1)所述kgc设置系统私钥sm和系统公钥ppub，完成系统建立。

步骤(2)所述用户u1随机选取k1∈[1,n-1]，计算p1＝k1g，发送p1到用户u2。

步骤(3)对于i＝2,3,…,n-1，所述用户ui在收到pi-1后随机选取di,ki∈[1,n-1]，计算pi＝(di)^-1pi-1+kig，发送pi到用户ui+1。

步骤(4)所述用户un在收到pn-1后随机选取dn,kn∈[1,n-1]，计算pn＝(dn)^-1pn-1+kng，发送pn到kgc。

步骤(5)所述kgc根据所述用户id和pn为用户生成部分私钥s0，发送s0到用户un。

步骤(6)所述用户un计算sn＝dn(kn+s0+1)(modn)，qn＝(dn)^-1g，发送sn和qn到用户un-1。并将dn作为用户un的私钥保存，将qn作为用户un的公钥参数保存。

步骤(7)对于i＝n-1,n-2,…,2，所述用户ui计算si＝di(ki+si+1)(modn)，qi＝(di)^-1qi+1，发送si和qi到ui-1。并将di作为用户ui的私钥保存，将qi作为用户ui的公钥参数保存。

步骤(8)所述用户u1计算d1＝(k1+s2)^-1(modn)，q1＝(d1)^-1q2，将d1作为用户u1的私钥保存，将q1作为用户u1的公钥参数保存。

本实施例生成的共享公钥为q＝((d1d2…dn)^-1–1)g，公众用户可以按无证书公钥密码体制的算法根据用户标识id和部分公钥计算用户的共享公钥，符合无证书公钥密码体制的特征。

图2所示为用户u1,u2,…,un联合对一个消息进行签名的实施流程。

有关椭圆曲线和密钥的记号如前，各参数的选择符合国密sm2算法标准的要求。假定待签名的消息为m，e＝h(z||m)，其中z为用户标识和公钥信息。多方联合签名按以下步骤实施。

步骤(9)所述用户u1计算摘要值e，再随机选取k1∈[1,n-1]，计算r1＝k1q1，发送e和r1到用户u2。

步骤(10)对于i＝2,3,…，n-1，所述用户ui在收到ri-1后随机选取ki∈[1,n-1]，计算ri＝ri-1+kiqi，发送e和ri到用户ui+1。

步骤(11)所述用户un在收到rn-1后随机选取kn∈[1,n-1]，计算rn＝rn-1+knqn。

步骤(12)设rn＝(x1,y1)，所述用户un计算r＝(e+x1)(modn)，sn＝kn+rdn(modn)，生成部分签名(r,sn)，发送部分签名(r,sn)到用户un-1。

步骤(13)对于i＝n-1,n-2,…,2，所述用户ui在收到用户ui+1的部分签名(r,si+1)后，首先验证该部分签名。若验证通过，再计算si＝ki+si+1di(modn)，生成部分签名(r,si)，发送部分签名(r,si)到用户ui-1。

步骤(14)所述用户u1在收到用户u2的部分签名(r,s2)后，首先验证该部分签名。若验证通过，计算s＝k1+s2d1–r(modn)，输出签名(r,s)。

上述实施例仅从原理上描述了本发明的内容，任何对本发明实质内容所作的数学上的变形和修饰都包含在本发明专利的保护范围。