基于中介中心性的网络传播节点影响力发现方法与流程

本发明涉及的是一种网络传播节点影响力发现方法。

背景技术：

随着互联网技术的飞速发展，社交网络的概念已不再仅仅局限于现实生活中，更体现在互联网社交平台中，互联网社交平台也逐渐成为了当今信息传播的主要渠道。随着社会以及社交网络逐渐呈现出网络化趋势，引发的“社交网络革命”(Social Network Revolution)，与“移动革命”(Mobile Revolution)、“互联网革命”(Internet Revolution)并称为新时期影响人类的三大革命。社交网络传播节点影响力发现是社交网络分析里一个关键的研究课题。社交网络传播节点影响力发现的目的，是利用现有的社交网络关系，挖掘出社交网络中影响力最大的Top-K节点集合。在当今社交网络中，节点影响力的发现已经逐步被应用于现实生活和在线社交平台中，其在舆情监控，市场营销，疾病防治，信息传播等领域都有了广泛的应用。

中介中心性算法在衡量一个节点在整个社交网络中的关键性和影响力有着较为精准的效果，但是其度量的精准度仍有提高的空间，并且时间复杂度较大也是其缺点之一。在度量结果的精准度上，缺点一：经过同一节点不同长度的最短路径以及在最短路径中节点位置不同都做同一处理；缺点二：偏重节点在全局网络中的影响力，忽略了节点在局部网络中的影响力。

传统的中介中心性对经过同一节点不同长度的最短路径以及节点在最短路径中位置不同都作为同一处理，但是信息在网路的传播中会发生信息量的衰减，所以经过同一节点不同长度的最短路径以及节点在最短路径中位置不同都不应当做同一处理。

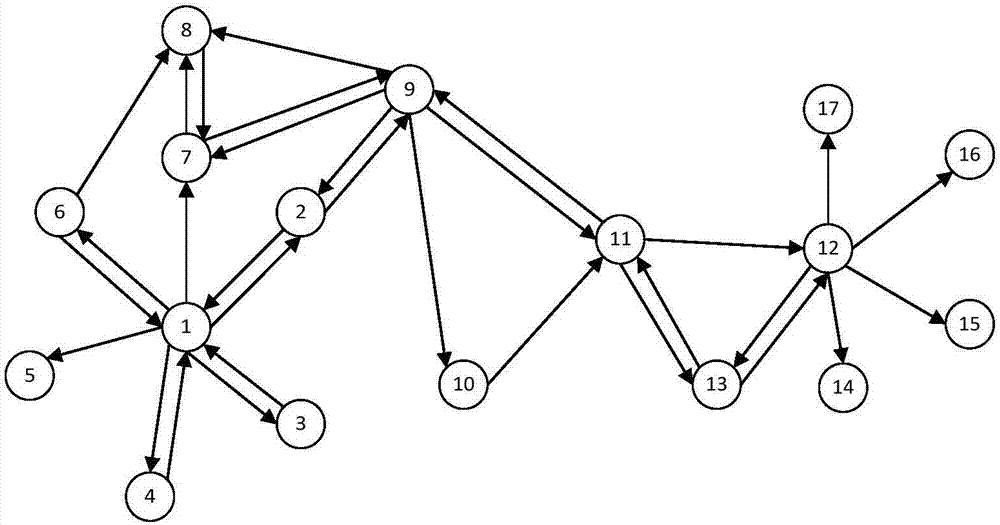
例如图1中，经过节点V11的从节点V9到节点V15的最短路径为P1(9-11-12-15)，经过节点V11的从节点V2到节点V15的最短路径为P2(2-9-11-12-15)，对于路径P1和P2，P1的路径长度为4，P2的路径长度为5，信息从开始节点到达路径结束节点距离越长，信息衰减越大，因此路径两条路径在对V11节点影响力有着不同的效果。又例如图1中，经过节点V11两条最短路径P3(2-9-11-12)和P4(10-11-12-15)，其中节点V11在路径P3中所处的位置为路径中的第三个节点，在P3中的位置是第二个节点，有信息传播衰减理论可知，相同信息到达在同一节点所经过的路径越长信息的衰减越大。

传统中介中心性算法在衡量一个节点在全局网络中的影响力和重要性即使有着不足，但是目前该方法对于衡量节点在全局网络中的影响力仍是比较好的算法之一。由于传统中介中心性是从全局角度出发衡量了一个节点的影响力，其必然会忽略节点在局部的影响力。著名的三度影响力原则指出，节点三度之内的邻居节点受该节点的影响较大，所以节点的局部影响力是传统中介中心性所没有体现的。

技术实现要素：

本发明的目的在于提供一种能够解决传统中介中心性算法在度量节点影响力上的不足的基于中介中心性的网络传播节点影响力发现方法。

本发明的目的是这样实现的：

首先遍历任意两点间的最短路径，获得路径集合δij；

针对任意两点间的路径P属于δij，对路径P中的每一个节点u计算DBC(u)ij,以及Loc(u)ij，其中DBC(u)ij＝((1-βPath[i][j])/1-β)*((Path[i][j]-Pos[u][i][j])/Path[i][j])，其中Path[i][j]代表路径P的长度，Pos[u][i][j]代表节点u在路径中的位置，β为衰减因子，Loc(u)＝Loc(u)∪节点i；

遍历所有路径结束后在遍历图中每一个节点u，计算DLBC[u]＝αDBC[u]+(1-α)(|Loc(u)|/n，α为调节因子，并将所有节点的DLBC值从大到小排列；

输出整个DLBC排序后的数组。

本发明还可以包括：

1、DBC(u)通过以下公式计算：

其中：

式中δ_ij为从节点i到节点j的最短路径，|δ_ij|为从节点i到节点j的最短路径的长度，δ_ij(u)为经过u的从i到j的最短路径，P_u(i,j)为节点u在δ_ij(u)上的位置，S(t)为信息传播衰减公式，W_u(i,j)为节点在δ_ij(u)中的重要性，DBC(u)为加入最短路径差异化因子后的中介中心性度量出的影响力大小。

2、Loc(u)通过如下公式计算：

其中δ_ui为从节点u到节点的最短路径，|δ_ij|为从节点i到节点j的最短路径的长度。

3、取调节因子α为0.7。

为了解决传统中介中心性算法在度量节点影响力上的不足，本发明提出了基于局部因子的差异化中介中心性算法(Different Betweeness Centrality Algorithm Based on Local Factors，DLBC)，从对不同长度的路径和节点的不同位置出发提出了差异化思想，并结合节点局部影响力作为对节点全局影响力的补充和纠偏。

(1)最短路径差异化处理的基本思想是根据最短路径的长短和节点所在最短路径的位置，结合信息衰减理论，对每条不同的最短路径都做差异化的处理。本发明提出的算法认为，信息每传播一次，由于噪音等原因，信息会有所衰减。当路径长度过长时，信息的衰减程度已经不能够表述原信息的含义，本发明规定长度超过阈值L的路径对节点影响力度量的影响可以忽略不计，因此长度超过L的最短路径无需计算在内，这样减少了最短路径的计算量，在一定程度上降低了时间的复杂度。根据以上介中心性算法优缺点的分析，做了如下改进：

①对于最短路径δ_ij(从i到j的最短路径)，|δ_ij|为最短路径的长度，对该条路径，通过信息传播衰减公式得知，信息从i传播到节点j时，信息已经衰减为S(|δ_ij|)，最短路径长短不同，衰减程度也不同，当路径长度超过L时，放弃该条路径。

②对于节点V_u，其位于δ_ij(u)(从节点i到节点j并经过节点u的最短路径)的第w跳的位置，w越小，则节点位置重要性越大，反之，位置重要性越小，本发明通过最短路径长度减去节点的所在位置后的结果与最短路径长度的比值，作为衡量该节点位置重要性的标准，若该比值越大，位置越重要。

根据以上两点的分析和改进，本发明提出的公式见式(1)。

其中：

式中δ_ij为从节点i到节点j的最短路径，|δ_ij|为从节点i到节点j的最短路径的长度，δ_ij(u)为经过u的从i到j的最短路径，P_u(i,j)为节点u在δ_ij(u)上的位置。S(t)为信息传播衰减公式，W_u(i,j)为节点在δ_ij(u)中的重要性，DBC(u)为加入最短路径差异化因子后的中介中心性度量出的影响力大小。

例如图1中，δ_V2V15(V₁₁)为经过节点V₁₁的从节点V₂到节点V₁₅的最短路径，其中一条最短路径为P₁(2-9-11-12-15)，以路径P₁为例，则|δ_V2V15(V₁₁)|为5，P₁₁(1,15)为3，W_V11(V₂,V₁₅)为3/5。

(2)为了补充中介中心性在节点局部影响力上的缺失，本发明提出了节点局部影响力因子，将传统的中介中心性算法与节点三度理论相结合，提出了基于中介中心性的局部影响力因子度量指标局部中心性LBC，LBC的基本思想为到某节点的，最短路径长度小于等于3的所有节点总数与网络节点总数的比值，由此可知，LBC越大则代表了该节点在局部能够影响到的节点的数量越大，局部影响力越大。其计算公式见式(4)。

其中δ_ui为从节点u到节点的最短路径，|δ_ij|为从节点i到节点j的最短路径的长度。

以图1中的节点V₉为例，最短路径长度小于等于3的集合为{1,2,3,4,5,7,8,10,11,12,13}，因此LBC(v₉)为11/17。

综合以上公式(1)和(4)，得出基于差异化和局部因子的中介中心性改进算法(DLBC)，DLBC即通过考量不同最短路径和节点所在最短路径的不同位置提高了传统中介中心性在节点全局影响力度量上的准确性，又通过提出的局部影响力度量算法弥补了传统中介中心性在节点局部影响力度量上的缺失。DLBC计算公式见式(5)。

DLBC(u)＝α·DBC(u)+(1-α)·LBC(u) (5)

式中DBC(u)见式(1)，LBC(u)见式(4),α为调节因子，经实验证明大小为0.7时，结果最为准确。

本发明的有益效果为：

本发明的方法充分发挥了传统中介中心性能够度量节点全局影响力的优势，并且通过对加入衰减因子以及节点重要程度因子，使算法在节点全局影响里度量上的精度得以提高。其次，本发明通过将距离节点最短路径长度小于等于3的节点数量与总体节点数量的比值，作为节点在局部影响力的度量，以此作为对节点全局影响力的补充，形成了节点综合影响力。最后在Wiki、Google+和Wiki样本数据集上，将DLBC与CC、LC、BC和DC四个算法进行了对比实验，证明了本发明提出的基于局部因子的差异化中介中心性算法的有效性。

附图说明

图1为社交网络图；

图2为Google+数据集上度中心性算法和F(t)的相关性；

图3为Google+数据集上中介中心性算法和F(t)的相关性；

图4为Google+数据集上各局部中心性算法和F(t)的相关性；

图5为Google+数据集上各紧密中心性算法和F(t)的相关性；

图6为Google+数据集上各基于局部因子的差异化中介中心性算法和F(t)的相关性；

图7为时间t＝4时Google+数据集上不同算法Top-K与传播范围的关系；

图8为Wiki数据集上度中心性算法和F(t)的相关性；

图9为Wiki数据集上中介中心性算法和F(t)的相关性；

图10为Wiki数据集上各局部中心性算法和F(t)的相关性；

图11为Wiki数据集上各紧密中心性算法和F(t)的相关性；

图12为Wiki数据集上各基于局部因子的差异化中介中心性算法和F(t)的相关性；

图13为时间t＝3时Wiki数据集上不同算法Top-K与传播范围的关系；

图14为本发明的实施流程图。

具体实施方式

下面结合附图举例对本发明作进一步描述。

(一)本发明的实施流程

结合图14，首先遍历任意两点间的最短路径，获得路径集合δij，针对任意两点间的路径P属于δij，对路径P中的每一个节点u计算DBC(u)ij,以及Loc(u)ij，其中DBC(u)ij＝((1-βPath[i][j])/1-β)*((Path[i][j]-Pos[u][i][j])/Path[i][j])，其中Path[i][j]代表路径P的长度，Pos[u][i][j]代表节点u在路径中的位置，β为衰减因子，Loc(u)＝Loc(u)∪节点i，遍历所有路径结束后在遍历图中每一个节点u，计算DLBC[u]＝αDBC[u]+(1-α)(|Loc(u)|/n，并将所有节点的DLBC值从大到小排列，输出整个DLBC排序后的数组。

(二)评价方法

主要是通过影响力发现算法度量出的影响力与节点真实影响力之间的相关关系来衡量算法的有效性，其中节点的真实影响力是通过SIR传播模型模拟节点影响力的传播得到的。如果算法度量出的影响力与节点真实影响力有明显正相关关系，则说明该影响力度量算法有效，正相关关系越明显，算法效果越好。

通过取不同的Top-K节点集合，模拟节点的传播，与其他算法比较相同Top-K下，不同算法度量出的Top-K节点集合的传播范围，传播范围越大的算法，节点影响力度量越精准。同时，本发明还采用了对比不同算法度量出的Top-10节点集合随着时间的推移节点影响力的传播范围，以此来对比不同算法的精准度，同一时间传播范围越大的算法，影响力度量越精准。

(三)结果及分析

采用二个不同数据集，分别为Google+和Wikipedia完整数据集，本发明提出的算法中衰减参数β为0.8，允许最长最短路径L为45，信息在长度大于45的路径上传播时，大于45的节点收到的信息已经可以忽略不计。分别将本发明提出的DLBC算法与接近中心性(CC)、局部中心性(LC)、中介中心性(BC)和度中心性(DC)做了对比分析。

图2-图6表示了DC，BC，LC，CC和DLBC五个算法与F(t)的关系，从图中散点图的走势可以很容易的得出DLBC和CC的结果较为相似，随着中心性度量的增大，节点相关性也逐渐增大，与节点真实的传播影响力较为接近。DC和BC算法都是从节点的全局影响力或者局部影响力某一个角度出发，所以点分布比较散乱，中心性度量的大的节点与中心性度量小的节点相关性关系相对不明显。LC算法考虑了节点的邻居以及邻居的邻居数量作为节点影响力的度量，因此相对DC和BC度量标准较为单一的算法效果较好，但是不如综合影响力算法DLBC和算法时间复杂度较高CC算法，LC算法的中心性和F(t)正相关性趋势同样不明显。由Google+数据集上正相关性实验可以得出：DLBC算法的相关性较好，度量精准度较高。

图7表示了DC，BC，LC，CC和DLBC五个算法在选择不同Top-K值时，传播时间t＝4时节点影响力的传播范围。从图7中很明显的看出本发明提出的DLBC算法在k取不同值时传播范围较其他算法大。与CC相比，由于CC算法考虑了节点到网络中其他节点的最短距离的总和，在一定程度上缺失了节点局部影响力，因此在Top-K节点较少的传播初期与DLBC的差距较为明显，但随着Top-K节点数量的增加，差距逐渐减少，从图7上可以看出，在t＝4时，k<＝40时，与DLBC的差距较为明显，在K>＝40时差距逐渐减少。DC算法在t＝4，k<＝54时，较BC算法好，在节点影响力传播初期，传播范围主要在网络的局部，DC算法有比较好的优势。LC算法效果在5个算法中效果居中，随着Top-K节点的增加，逐渐接近DC，比DLBC和CC较差。通过图7，能够很明显的得出：在去不同Top-K值时，DLBC算法均相对其他算法有效。

通过图8-图12可以看出在比较复杂的网络中，DC和BC算法与F(t)的关系已经变的十分模糊，两个算法的散点图中点分布比较分散无明显相关关系，度量效果较差。LC算法在局部中心性与F(t)相对DC和BC算法有较明显的正相关关系，但是与CC和DLBC相比正相关关系较弱。CC算法在紧密中心性小于800时与F(t)的正向关系较为明显，但是在紧密中心性大于800时点分布相对分散没有明显关系。DLBC在五个算法中与F(t)正相关关系最为明显。通过以上分析，在该数据集上DLBC算法最为有效。

图13反映了在Wiki数据集上传播时间t＝3时，不同算法的Top-K与影响力传播范围的关系。从图中可以看出DLBC比其他算法在0-200的Top-K节点上的传播范围均是最广泛的。CC算法次之，与LC算法较为接近。DC算法由于传播时间较短，其传播范围优于BC，传统的BC算法在五个算法中表现最差，主要原因是传播时间t较小，处于节点影响力传播初期，而BC从全局角度度量节点影响力，在节点影响力传播后期较DC更有优势。

(四)结论：

目前社交网络节点影响力发现的研究方向是提高算法结果的精准度。虽然目前对社交网络传播节点影响力发现的研究有很多，但是既能够在保证算法结果精准度的同时，还能够有较好执行效率的研究成果相对较少。针对传统的中介中心性提出了基于差异化和局部因子的两点改进，大大提高了传统中介中心性算法的结果精准度。通过在Wiki、Google+和Wiki样本数据集上进行相关性等试验，与其他常用节点影响力发现算法进行对比，验证了本发明提出的基于差异化和局部因子的中介中心性节点影响力发现算法的有效性。本发明主要内容如下：

本发明基于传统中介中心性算法，提出了基于局部因子的差异化中介中心性算法(DLBC)。该算法充分发挥了传统中介中心性能够度量节点全局影响力的优势，并且通过对加入衰减因子以及节点重要程度因子，使算法在节点全局影响里度量上的精度得以提高。其次，本发明通过将距离节点最短路径长度小于等于3的节点数量与总体节点数量的比值，作为节点在局部影响力的度量，以此作为对节点全局影响力的补充，形成了节点综合影响力。最后在Wiki、Google+和Wiki样本数据集上，将DLBC与CC、LC、BC和DC四个算法进行了对比实验，证明了本发明提出的基于局部因子的差异化中介中心性算法的有效性。

尽管本发明通过不同的对比实验证明了本发明提出的算法是有效的，但是不等概率随机游走数据抽样算法和基于局部因子的差异化中介中心性算法均还存在着不足有待进一步的研究和改进。具体问题如下：

基于局部因子的差异化中介中心性算法虽然在节点的全局和局部影响力都做了考量，提高了影响力度量的准确性，同时也通过在样本上进行实验降低了执行效率，但是其算法本身的时间复杂度过高的问题仍然没有解决。在之后的研究和工作中，可以借鉴Brande基于单源最短路径理论提出的快速计算节点中介中心性的算法，从算法本身出发降低时间复杂度。