一种DCO‑OFDM系统中最优直流偏置的确定方法与流程
本发明涉及可见光通信技术领域,尤其涉及一种可见光dco-ofdm通信系统中最优直流偏置的确定方法。
背景技术:
可见光通信是一种通过光辐射传输负载信息的新兴技术,以其诸多的优点,成为近年来无线通信领域研究的热点之一,是未来无线接入方案中针对射频技术最有潜力的互补技术。ofdm是可见光通信高速传输的基本调制方法,其中dco-ofdm方案出现时间早,研究较为成熟,所以在目前大部分的可见光实物系统的实现都是采用的该方案。dco-ofdm需要加入直流偏置来降低裁剪噪声,但过大的直流偏置会因直流而浪费了过多的能量,降低了能量效率,因此需要寻找最优的直流偏置系数。
目前关于dco-ofdm系统直流偏置确定方法的讨论主要在awgn信道下进行讨论,因为:第一,awgn信道简单,计算推导容易;第二awgn信道也很重要,因为光信道的低通特性,我们可以选取平坦区,此时就是近似于awgn信道了,或者也可以通过均衡和预均衡的方式将信道补平;第三,得到awgn信道下的结果时,可以再由此基础推导频率选择性信道下的结果。
在dco-ofdm早期的研究中,都是加入足够大的直流偏置以消除裁剪噪声。vishwanath等人从信息论的角度论证了完全不削波dco-ofdm系统的频谱效率会随着子载波数的增加而减小。armstrong等人尝试加入较小的直流偏置并裁剪负值得到单极性信号。dimitrov考虑了光功率限制下给定误比特率的信噪比最小化问题。chenl在光功率限制和电功率限制下使用了黄金分割法求解,但不能保证是最优的。zhangmingxuan说明了该优化问题是一个非凸问题。lingxintong证明了单边裁剪时该问题是拟凸问题,并给出了该问题的闭式解。
但是上述方案在研究dco-ofdm系统的最优直流偏置时,大多研究的是单边裁剪。但考虑到led的非线性特性,单边裁剪时会对led的动态范围要求比较大,因此双边裁剪的研究也很有必要。双边裁剪就是不但将负值部分裁剪掉,并且将过大的正值部分也裁剪掉,对称双边裁剪就是两端的裁剪是相对称的。
技术实现要素:
发明目的:本发明针对现有技术存在的问题,提供一种dco-ofdm系统中最优直流偏置的确定方法。
技术方案:本发明所述的一种dco-ofdm系统中最优直流偏置的确定方法包括:
(1)对于给定的光信噪比γo进行归一化,得到归一化光信噪比γo,n,其中,
γo,n=γo|h|2
式中,h表示信道的频率响应,对于awgn信道为一个常数;
(2)根据归一化光信噪比γo,n建立对称双边裁剪时最优相对直流偏置系数μ满足的非线性方程
(3)用牛顿迭代法求解f(μ)的根,具体步骤为:
a、设置迭代次数i=0,μ0=0,根据需求设置容忍误差ε,ε>0;
b、计算d=f(μi)/f′(μi);
c、令μi+1=μi-d;
d、若|d|≥ε,则令i=i+1,并执行步骤b;若|d|<ε,则迭代结束,此时的μi+1即为最优相对直流偏置系数μ;
(4)根据最优相对直流偏置系数μ计算得到最优直流偏置量idc,其中,
idc=μσs
式中,σs为裁剪直流偏置前信号的方差。
有益效果:本发明与现有技术相比,其显著优点是:本专利提出了一种对于dco-ofdm系统的对称双边裁剪情况时的最优直流偏置的确定方法。该方案的复杂度较低,易于实现,可以在较低复杂度情形下得到对可见光dco-ofdm通信系统双边进行对称双边裁剪时的最优直流偏置,使在给定的光信噪比下,系统的可达速率最高。
附图说明
图1是64qam调制下对称双边裁剪误码率与μ的关系图。
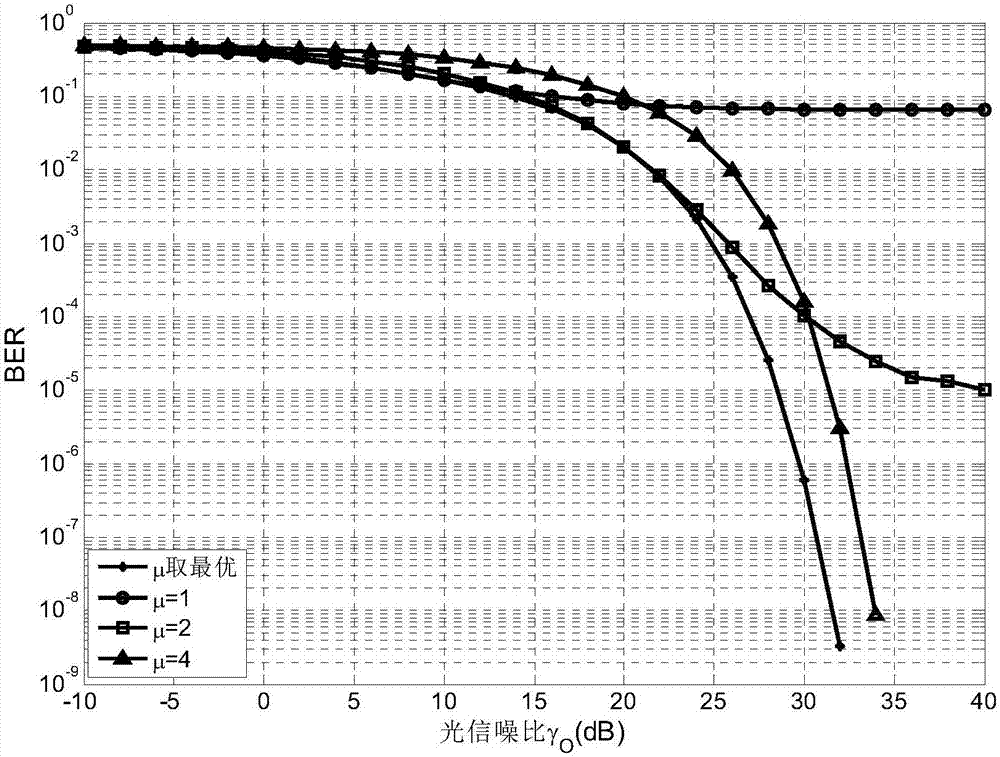
图2是16qam调制下对称双边裁剪误码率与γo的关系图。
具体实施方式
本发明应用于可见光dco-ofdm系统中,并对信号进行对称双边裁剪时的情况。本发明给出的方法是在awgn信道条件下,当系统不是awgn信道时,可以通过选取平坦区或者用补平的方法得到awgn信道。
一、技术问题
假设裁剪前的信号为s(n),裁剪后的信号为sc(n),而裁剪后再加上直流偏置的信号为sdc(n),直流偏置为idc,则
sdc(n)=sc(n)+idc(2)
在光通信中由于进行强度调制,同时也要考虑照明因素,所以光强也是很重要的变量,同时由于需要考虑直流偏置带来的能量浪费,因此定义光信噪比γo为
式中,
由于加入的直流偏置为一个与n无关的常量,而
fft(idc)=idcnδ(k)(4)
式中,n表示fft的点数,δ(·)表示冲激函数。根据式(4)可知,加入直流偏置在频域只影响0号子载波上的信号,而在dco-ofdm中,0号子载波作为虚拟子载波使用,是不传输信号的,关注点可以放在sc(n)上。
根据中心极限定理,当fft点数选取足够多以及一帧中ofdm符号足够多时,s(n)服从均值为0,方差为
因此可根据bussgang定理:高斯输入的非线性系统的输出可以表示成两个不相关的可分离部分之和,一部分是与输入信号成正比的有用信号,另一部分是与信号不相关的非线性干扰,即
sc(n)=αs(n)+d(n)(5)
式中,d(n)为非线性干扰,
式(5)的频域为
因为加上直流偏置只影响0号子载波,不考虑加上直流偏置,接收信号为
h(k)为信道频率响应,z(k)为噪声。
定义相对直流偏置系数μ为
引入sndr,这就是考虑了裁剪噪声后的系统实际信噪比,在迫零均衡时,有
式中,p(k)为分配到每个子载波上的功率,
当平均分配时,有
式中,nc为ofdm子载波数,ndata为使用数据子载波数。
系统可达速率为
式中,ω为使用子载波的集合,γ为香农信道容量与目标物码率下可达速率之间的信噪比间隔。那么,最优直流偏置的问题就转化为在相应的γo下,使r最大时的μ的取值,即
因为awgn信道时平坦的,|h(k)|2是一个常数,因此采取平均功率分配是最优的。
式(10)可以改写为
式中,因为每个子载波上的功率以及频响相同,在这里就将下标k给去掉了。由于每个子载波上的sndr相同,因此由式(12)以及(13),该问题可以表述为:
sndrn为式(14)中sndr去掉系数
为了叙述方面,将后面的章节中出现的函数在这里先进行定义,为
我们具体推导计算sndrn,过程如下:
利用对称双边裁剪时s(n)与sc(n)的对称性得到其为0均值,得
e(d(n))=e(sc(n))=e(s(n))=0(20)
由上式知,在给定μ的情况下,对称双边裁剪时裁剪噪声功率与信号噪声功率成正比。
e(sdc(n))=idc=μσs(22)
在给定γo的情况下,定义归一化光信噪比γo,n=γo|h|2,可得
下面再推导最优直流偏置满足的非线性方程,过程如下:
上式中为了简洁起见,用q、
g(μ)对μ求导,得到
由上式可知g(μ)是关于μ的单减函数,由于g(0)=0,因此在μ∈(0,+∞)内,g(μ)<0,又因为在μ∈(0,+∞)时,q(μ)<1/2,可知1-2q(μ)>0,因此式(24)可表示为
上式中λ>0为一个正系数。求解最优直流偏置的问题转化为求f(μ)的根。因为
f(μ)是关于μ的减函数,因此此时f(μ)有且只有唯一的一个根,而且由式(28)可知,
二、技术方法
本发明的dco-ofdm系统中最优直流偏置的确定方法,具体包括以下步骤:
(1)对于给定的光信噪比γo进行归一化,得到归一化光信噪比γo,n,其中,
γo,n=γo|h|2
式中,h表示信道的频率响应,对于awgn信道为一个常数;
(2)根据归一化光信噪比γo,n建立对称双边裁剪时最优相对直流偏置系数μ满足的非线性方程
(3)用牛顿迭代法求解f(μ)的根,具体步骤为:
a、设置迭代次数i=0,μ0=0,根据需求设置容忍误差ε,ε>0;
b、计算d=f(μi)/f′(μi);
c、令μi+1=μi-d;
d、若|d|≥ε,则令i=i+1,并执行步骤b;若|d|<ε,则迭代结束,此时的μi+1即为最优相对直流偏置系数μ;
(4)根据最优相对直流偏置系数μ计算得到最优直流偏置量idc,其中,
idc=μσs
式中,σs为裁剪直流偏置前信号的方差。
以上所揭露的仅为本发明一种较佳实施例而已,不能以此来限定本发明之权利范围,因此依本发明权利要求所作的等同变化,仍属本发明所涵盖的范围。
- 还没有人留言评论。精彩留言会获得点赞!