一种SOQPSK信号的解调方法与流程

本发明属于soqpsk信号解调技术领域，具体涉及一种soqpsk信号的解调方法。

背景技术：

soqpsk信号是将正交相移键控的频偏成形脉冲由关于冲激的函数改为连续的函数。soqpsk拥有oqpsk的恒包络和cpm的连续相位特性，使得其在传输器件的使用上有更大的选择性(如使用非线性放大器件)，同时节省了带宽资源。其调制方式除了常规的预编码结合频率成形脉冲进行调制外，还有更为优秀的8-xtcqm方式。针对使用viterbi算法的解调方式，来实现最大似然序列检测，对于部分响应soqpsk信号，随着频率整形脉冲记忆长度的增加，所需要的匹配滤波器的个数和维特比译码的网格状态数呈指数级增长，因此运算过程复杂、实现器件的要求苛刻。

技术实现要素：

本发明的目的在于：针对现有的解调方式运算过程复杂、实现器件的要求苛刻的问题，提供一种soqpsk信号的解调方法，利用soqpsk信号的相位特性，通过理论推导演算得出简易的译码方式并通过仿真得到预期的实验结果，大大简化了传统解调过程中繁琐的译码方式，降低了解调成本。

为了实现上述目的，本发明采用的技术方案为：

一种soqpsk信号的解调方法，soqpsk信号通过同步载波进行正交化处理，将携带信息的i分量和q分量从高频信号中剥离出来，再利用soqpsk的相位特性进行信号相似度比对得到i分量和q分量的信息码，将得到的两组信息码输入到译码器中获得原始码。

优选地，所述的信号相似度比对包括将所述的i分量或q分量通过与基础波形乘积后积分，再与基础波形自身乘积的积分做比较，得到的差值作为差异度的量化值，通过最小的差异度量化值锁定该基础波形所对应的信息码。

优选地，正交化处理后分量i和q分别进入两组用于所述的信号相似度比对的信号相似度对比模块，每组信号相似度对比模块中包含波形源于soqpsk信号的相位特性的基础波形，两组信号相似度对比模块中涵盖soqpsk信号的所有表现形式；

分量i和q分别进入两组信号相似度对比模块后，进行所述的信号相似度比对，得到所述的最小差异度量化值所在的基础波形所对应的信息码。

优选地，每组信号相似度对比模块包括多个通道，每个通道中对应输入一种所述的基础波形，两组信号相似度对比模块包含的多种基础波形，涵盖soqpsk信号的所有表现形式。

优选地，每组信号相似度对比模块包括8个通道。

优选地，所述的每个通道中包括一乘法器、两积分器和一个减法器，所述的乘法器用于输入分量信号与基础波形的相乘，所述的其中一个积分器用于乘法器输出信号的积分，所述的另一个积分器用于基础波形平方的积分，所述的减法器用于将两个积分器的输出相减且差值作为所述的差异度的量化值。

优选地，所述的每个通道中包括两个乘法器、两个积分器和一个加法器，所述的其中一个乘法器用于输入分量信号与基础波形的乘积，所述的其中一个积分器用于将乘积后的信号进行积分，所述的另一个乘法器用于将积分后的信号取反，所述的另一个积分器用于基础波形平方的乘积，所述的加法器用于取反后的信号与基础波形平方的乘积进行相加，相加后的值作为所述的差异度的量化值。

优选地，所述的译码器采用8-xtcqm的译码方式，将所述的i分量和q分量的信息码通过8-xtcqm的译码得到原始码。

由于采用了上述技术方案，本发明的有益效果是：

本发明将接收到的soqpsk信号被同步载波进行正交化处理后，经过正交化处理的信号,通过与基础波形的乘积后积分,再与基础波形的自身乘积积分做比较，将数值作为译码的依据来获得译码结果，该方式实现了高效且简易的解调译码过程，减少了传统解调译码方式的复杂运算过程和实现器件的要求苛刻的问题。

附图说明

图1是本发明的实施例1的soqpsk解调的流程图。

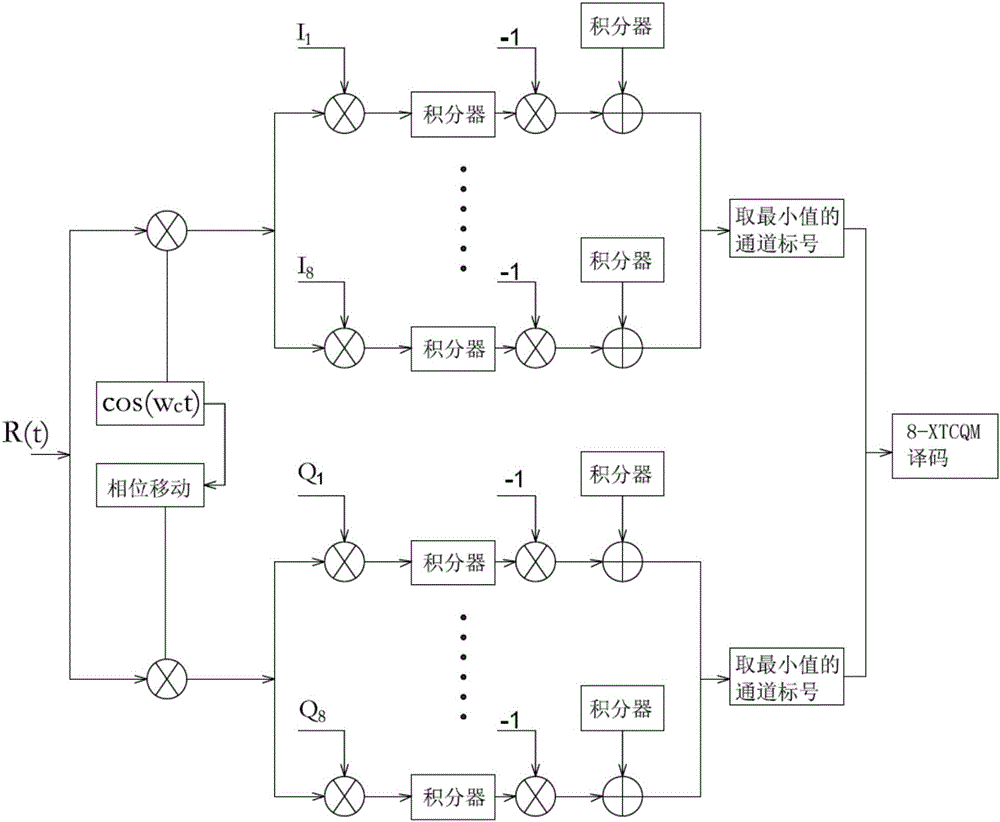
图2是本发明的实施例2的soqpsk解调的流程图。

图3是本发明的8-xtcqm的预编码流程图。

具体实施方式

实施例1：

参照图1，本发明的soqpsk信号的解调方法，解调时按照8-xtcqm的思路是指：解调方式可依据8-xtcqm基础波形调用的方式，将接收到的信号与基础波形进行相关运算来进行解调。

接收到的已调信号：r(t)＝i(t)sin(wct)+q(t)sin(wct)；

该信号忽略了其他干扰因素，如噪音，多普勒频移等，本申请重点主要集中在解调方式上，故对其他干扰因素不做过多分析。接收到的信号的表达形式来源于8-xtcqm调制方式，由于表达形式所实现的调制效果与常规方式一致，故该表达式可以视为soqpsk调制的统一表达式，该表达式在进行解调理论推导时更便于处理。

将接收到的波形进行正交化处理以便后续的信息分量i,q的剥离，正交化处理所使用的混频信号的频率为同步载波频率。

接收到的信号分别通过混频信号为cos(wct)的i通道和混频信号为sin(wct)的q通道，

将接收到的信号送入两个混频器，频器所采用的频率为载波频率，两个混频器相位相差90°，其表达式为cos(wct)和sin(wct)，通过混频表达式为cos(wct)的信号记为ri(t)；通过混频表达式为sin(wct)的信号记为rq(t)，通过这两路通道的信号表达式分别为：

i通道：ri(t)＝i(t)cos²(wct)+q(t)sin(wct)cos(wct)；

q通道：rq(t)＝i(t)sin(wct)cos(wct)+q(t)sin²(wct)。

ri(t)信号进入i分量对应的基础波形模块，该模块为8通道，每个通道中采取一种i分量对应的基础波形；rq(t)信号进入q分量对应的基础波形模块，该模块为8通道，每个通道中采取一种q分量对应的基础波形

在每个通道中信号会进过一个乘法器，一个积分器和一个减法器，减法器运算时还包括对基础波形平方积分的另外一积分器。

为避免描述混乱，现以i分量对应的基础波形模块中的一个通道来进行举例说明，其对应的基础波形为i′(t)。

乘法器的对象为ri(t)和该通道对应的基础波形i′(t)。通过乘法器的信号表达式为：

ci(t)＝i(t)i′(t)cos²(wct)+q(t)i′(t)sin(wct)cos(wct)

积分器的对象为c(t)，积分周期为两个码元周期。通过积分器的信号表达式为：

注意为了便于后续计算省去了di(t)里的系数0.5。

本文采用差值的方式来进行相似度比对，对比的标尺为基础波形自身乘积的积分，接下来通过理论推导和实际数据进行论证。

标尺的确定：m＝1,2,3,4,5,6,7,8，代表通道编号。

减法器的对象是di(t)和sim(t)，通过积分器的信号表达式为：

当i(t)和i′(t)相同时，wi′(t)＝0，即“当i(t)和i′(t)具有高度相似性时”是“wi′(t)＝0”的充分条件。

用matlab进行的全部可能赋值运算，通过得到的数据结果得知当且仅当i(t)＝i′(t)时其值为0，证明了“当i(t)和i′(t)具有高度相似性时”是“i(t)和i′(t)＝0”的必要条件。

由最小的wi可得到当前通道所对应的基础波形，该基础波形与接收到信息的i分量信息码最为接近，故该基础波形所对应的信息码即可视为接收到信息的i分量的信息码。

同样的，进行上述流程可以得到接收到信息的q分量的信息码。

至此，得到了接收到信息i分量的信息码和接收到信息i分量的信息码；将得到的两组码元并行输入本发明所搭配的8-xtcqm译码器便可获得原始码。

本文所提出的解调译码方法用较为简单的减法运算代替了复杂的viterbi和其他算法，通过运算推导和实际验证证明了方法的合理性，简化了解调过程，节省了解调成本和降低解调难度。

实施例2：

本实施例与实施例1的不同之处在于，本实施例的每个通道中有两个乘法器，两个积分器和一个加法器，以下通过具体实施方法进行说明：

在常规的soqpsk调制解调中，往往从最原始的角度去处理，如先进行预编码将原始码从二进制通过特殊转换关系变为三进制的信息码，再结合频偏脉冲成形函数得到soqpsk的相位函数，然后将相位函数放入调相信号的通用函数中以此得到soqpsk的已调信号。这种调制思路使得解调处理异常艰难。

在8-xtcqm调制方式出现后，soqpsk的独特相位特性开始在调制中得到充分利用，采用调用的方式极大地提高了调制效率，降低了调制难度，但在解调过程中仍采取了一系列复杂的算法来进行解调，如最常见的viterbi算法，要求巨大的运算量同时要提供状态转移的概率等一系列参数。

在常规解调中虽然用到了多个通道和基础波形调用的方式，但并未将soqpsk的相位特殊性作为解调的突破点。

参考图2，待处理的接收信号为r(t)，其中所存在的噪声，频偏等外部影响因素暂不考虑。

将接收到的信号送入两个混频器，混频器所采用的频率为载波频率，两个混频器相位相差90°，其表达式为cos(wct)和sin(wct)，通过混频表达式为cos(wct)的信号记为ri(t)；通过混频表达式为sin(wct)的信号记为rq(t)，通过混频器的两路信号有着各自的任务：

从ri(t)中获取i分量对应的信息码；从rq(t)中获取q分量对应的信息码。

参考图2，将ri(t)送入涵盖i分量所有可能的基础波形的8个通道，这8个通道用于完成与ri(t)中i分量进行相似度对比，获得最大相似度(即最小差异度量化值)的通道表明该通道中的基础波形与ri(t)中i分量最为相似，该基础波形所对应的信息码即可作为ri(t)中i分量的信息码。

将rq(t)送入涵盖q分量所有可能的基础波形的8个通道，这8个通道用于完成与rq(t)中q分量进行相似度对比，获得最大相似度(即最小差异度量化值)的通道表明该通道中的基础波形与rq(t)中q分量最为相似，该基础波形所对应的信息码即可作为rq(t)中q分量的信息码。

在soqpsk中i分量所对应的可能的波形有且仅有8种，如图2所示i1，i2，i3,i4,i5,i6,i7,i8,为每一种基础波形建立一个相似度对比通道，每个通道中有两个乘法器，两个积分器和一个加法器。

在soqpsk中q分量所对应的可能的波形有且仅有8种，如图2所示q1,q2，q3,q4,q5,q6,q7q8为每一种基础波形建立一个相似度对比通道，每个通道中有两个乘法器，两个积分器和一个加法器。

参照图2，所示ri(t)分别通过8路通道中的乘法器后得到：

cim(t)＝i(t)im(t)cos²(wct)+q(t)im(t)sin(wct)cos(wct)，其中m＝1，2,3,4,5,6,7,8。

通过二倍角公式可得：

参考图2，所示rq(t)分别通过8路通道中的乘法器后得到：

cqn(t)＝i(t)qn(t)sin(wct)cos(wct)+q(t)qn(t)sin²(wct)，其中n＝1，2,3,4,5,6,7,8。

通过二倍角公式可得：

载波频率是码元频率的整数倍，且远远大于码元频率，携带有载波分量的乘积项在两个码元周期内便可将其消除，之所以使用两个码元周期是由于在设置基础波形时统计的是两个码元周期的函数。利用混频器对信号变频，再结合积分器对信号定限积分以达到低通滤波的效果。

cim(t)通过积分器后得到其中m＝1，2,3,4,5,6,7,8,(注：省略了系数0.5)。cqn(t)通过积分器后得到其中n＝1，2,3,4,5,6,7,8,(注：省略了系数0.5)。

基础波形的数据可存储在存储器中，在解调时调用即可，其表达式为其中m＝1，2,3,4,5,6,7,8；其中n＝1，2,3,4,5,6,7,8。

8路dim(t)和8路dqn(t)分别经过用于取反的乘法器后与对应通道的sim(t)，sqn(t)进行加法操作，得到8个和8个通过两组比较器得出wtm(t)中最大值所对应的m和wqn(t)中最大值所对应的n。

将得到的m，n送入8-xtcqm译码器，即可获得原始码，其具体流程如下：

mi0＝[(m-1)/4]，mi1＝[((m-1)-mi0)/2]，mi2＝(m-1)-mi0-mi1；

mq0＝[(n-1)/4]，mq1＝[((n-1)-mq0)/2]，mq2＝(n-1)-mq0-mq1；其中[]表示取整，[x]表示不超过x的最大整数。

kin-1＝mi2，kqn-1＝mq2，kin＝(1-2kin-1)kin-1，kqn＝(1-2kqn-1)kqn-1，kin表示当前时刻原始码的i值，kin-1表示下上个时刻原始码的i值；kqn表示当前时刻原始码的q值，kqn-1表示上一个时刻原始码的q值。

kin，kqn进行串并变换即可得到原始码。

该译码方式同时拥有检错功能，可以通过mi1＝mq1，mi0＝mq0是否成立来进行检错，其原理在8-xtcqm的预编码过程中有详细解释，参考图3。

该译码方式同时拥有校对功能，kin-1表示下上个时刻原始码的i值，通过比对上一个原始码中的i值来进行检错；同理kqn-1表示下上个时刻原始码的q值，通过比对上一个原始码中的q值来进行检错。

通过上文对本发明的详细描述，该解调方式在相似度比较处理和译码处理方面尽可能地利用了soqpsk信号的相位特性，使得解调过程难度大幅下降，在提出的解调方式中还包含了检错的功能，是常规解调方式所不具备的。

用matlab进行的全部可能赋值运算，通过得到的数据结果，如表1所示数据，第x行第y列的数值表示的运算结果，在这64个数值中，当x＝y时，得到最小值0。即是当且仅当i(t)＝i′(t)时，其值为0，证明了“当i(t)和i′(t)具有高度相似性时”是“wi′(t)＝0”的必要条件；表2所示数据，第x行第y列的数值表示为的运算结果，其验证思路同上，故不加赘述。

表1.的运算结果

表2.的运算结果