基于大尺度衰落信道信息的能效优化快速天线选择算法的制作方法

本发明设计的一种基于大尺度衰落信道信息的能效优化快速天线选择算法，属于移动通信技术领域。

背景技术

传统的分布式天线系统可以克服大尺度数量和阴影衰落造成的信道路径损失，能够在小区内形成良好的系统覆盖，解决小区能通信死角，提高通信服务质量。分布式mimo系统是分布式天线系统和mimo技术结合的产物。能转化干扰信号作为有用信号，从而提升频谱效率。由于其各方面优越的性能，使其越来越多地受到学术界和产业界的共同关注。并且随着移动通信技术的快速发展，无线接入速率越来越高，而可用的频谱资源却日益紧张，通信系统的能量损耗也急剧增加，这就促使降低系统能耗、提高系统能效为目的的绿色通信技术的快速发展，绿色通信成为通信领域的新的研究热点。因此，在分布式mimo系统架构上，可研究出一个有效的天线选择算法，能提高系统能效并且运算复杂度低。

人们对mimo系统中的天线选择算法已经有了较为成熟的研究，出现了穷举法、最大范数天线选择算法、递减算法、递增算法等经典的算法，以及在此基础上的各种改进算法。如何在有效降低运算复杂度的同时，提高分布式mimo系统的能量效率，就成为了本领域技术人员亟需解决的问题，对于分布式mimo系统而言，由于其天线数目多以及其信道衰落的特点，本发明在大尺度衰落信息算法的基础上结合能效逐增算法提高系统能量效率。

技术实现要素：

针对上述问题，本发明提供一种基于大尺度衰落信道信息的能效优化快速天线选择算法。利用基于大尺度衰落信道信息的分簇选择算法筛选出系统能量效率最大的ns个rau簇，再结合能效逐增算法优化每个rau簇的能量效率。最后，用ns个局部最优解来逼近全局最优解，达到系统能效优化且运算复杂度较低的目的。

本发明的目的在于提高分布式mimo系统的能量效率，降低运算复杂度。主要包括两个部分：基于大尺度衰落信道信息的分簇选择算法和能效逐增算法。通过分簇选择算法和能效逐增算法的结合使用，一方面降低了天线选择运算复杂度，另一方面提高了系统的能量效率。

本发明为解决上述技术问题采用以下技术方案：

一种基于大尺度衰落信道信息的能效优化快速天线选择算法，包括以下步骤：

步骤1，基于大尺度衰落信道信息的分簇选择算法从n个rau簇中筛选出ns个使系统能量效率最大的rau簇；

步骤2，基于能效最优算法优化ns个rau簇的能量效率，用ns个局部最优解来逼近全局最优解，得到使分布式mimo系统能效最优的信道矩阵以及系统最大的能量效率。

优选地，步骤1包括：

步骤1.1，初始化参数，所述参数包括信道矩阵h，迭代器i＝0，分布式mimo系统的rau个数n，系统最大能量效率ηtemp＝0，n个rau簇的位置以及系统能量效率最大的rau簇个数ns＝n；

步骤1.2，更新信道矩阵，得到新的信道矩阵h*；

步骤1.3，根据分布式mimo系统的下行能效表达式计算出最初的系统能量效率η，且令ηtemp＝η；

步骤1.4，更新参数：迭代器更新i＝i+1，判断此时迭代器数和rau个数n的大小，如果i>n，算法退出，否则继续下一步；

步骤1.5，迭代删除h^*的最后l列，即每次删除βn最小的rau，再比较删除前后的系统能量效率，最后选择出使系统能量效率最大的ns个簇；

步骤1.6，返回最后得到的ns，信道矩阵h*以及系统最大能量效率ηtemp。

优选地，步骤1.1中的所述参数还包括：用户接收天线m，每个rau上发射天线数l，路径损耗指数α，阴影衰落标准差sn，小区半径和移动台位置。

优选地，步骤1.2具体为：已知信道矩阵h，根据信道矩阵元素与大尺度衰落信道信息之间的关系，

其中dn表示第n个rau单元与终端间的距离，βn表示第n个rau簇与终端间的大尺衰落信道信息，是第n个rau簇的第l根天线与用户终端的第m根天线间的瞬时信道信息，

将大尺度衰落信息βn按照降序排列，得到新的信道矩阵h*，矩阵可表示为，

其中，βn<βn-1<…<β1。

优选地，步骤1.5具体为：

1.5.1，删除信道矩阵h*的最后i×l列，得到新的信道矩阵h^*；

1.5.2，令ns＝n-i，此时发射天线数为ns·l，根据分布式mimo系统功耗表达式得到总功耗pall，再根据下行能效表达式计算出新的系统能效η；

1.5.3，比较此时的η和ηtemp，

若η>ηtemp，则令ηtemp＝η，进入步骤1.6；

否则ηtemp不变，转回步骤1.4。

优选地，步骤1.5.2中的分布式mimo系统功耗表达式为

下行能效表达式为

其中，peq表示rau端上每根发射天线的发射功率，pe为n个rau簇的射频链路功耗，为定值，h是m×nl维的信道矩阵，δ²是噪声功率。

优选地，步骤2中基于能效最优的逐增算法优化系统能效，具体为：

步骤2.1，初始化参数：rau簇数目迭代器n＝1,2,…,ns，每个rau上发射天线数迭代器l＝1,2,…,l，第n的rau簇的系统能效可使rau簇系统能效最优的发射天线数lnum＝0；

步骤2.2，重构新的信道矩阵：基于步骤1.6得到的信道矩阵h*，将其重新构造得到新的

信道矩阵hs，且令n＝1；

步骤2.3，判断n与ns的大小，若n>ns，则算法退出；否则令l＝1，转下一步；

步骤2.4，优化每个rau簇内的能量效率；

步骤2.5，根据已优化的rau簇，得到可使该簇的能量效率达到最优的信道矩阵；

步骤2.6，判断n与ns的大小，如果n＝ns，根据步骤2.5得到的信道矩阵计算出系统能效，算法退出；否则令n＝n+1，重复步骤2.3至2.6；

步骤2.7，返回最终的最优信道矩阵，并计算出系统的最优能效。

优选地，步骤2.2中重新构造新的信道矩阵的方法具体为：

经过步骤1中分簇选择后的信道矩阵h*是m×nsl维，将矩阵h*中每个簇的列元素按元素和的大小成降序排列，得到新的矩阵hs，表示为：

其中，是m×l维矩阵，它表示第n个簇的信道矩阵，且根据元素和的大小成降序排列。

优选地，步骤2.4具体为：

2.4.1，判断l与l的关系，若l>l则转到步骤2.5，否则进入2.4.2；

2.4.2，取的前l列构成矩阵htemp并计算

如果令

否则和lnum不变，l＝l+1，重复步骤2.4。

优选地，步骤2.5具体为：根据步骤2.4得到的和lnum求得使第n的簇的能效达到最优的信道矩阵之后转到步骤2.6。

本发明技术方案的优点主要体现在：在有效降低运算复杂度的同时，提高分布式mimo系统的能量效率，与能效最优的穷举法相比，本算法能效趋近于它，但本算法的复杂度远远低于穷举法。

此外，本发明也为同领域内的其他相关问题提供了参考，可以以此为依据进行拓展延伸，运用于移动通信技术领域内其他的技术方案中，具有很强的适用性和广阔的应用前景。

总体而言，本发明所兼顾了实用性和创新性，具有很高的使用及推广价值。

附图说明

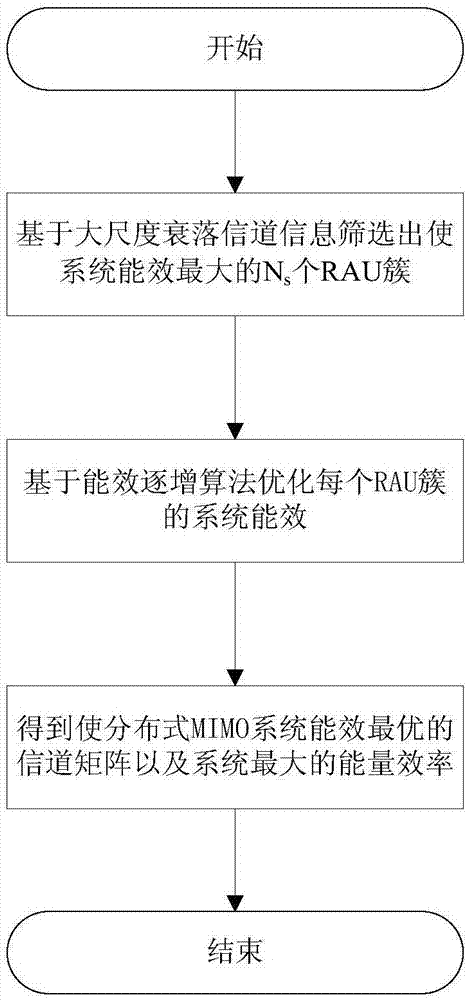
图1是本发明的系统流程图；

图2是本发明的分簇选择算法流程图；

图3是本发明的能效逐增算法流程图。

具体实施方式

本发明的目的、优点和特点，将通过下面优选实施例的非限制性说明进行图示和解释。这些实施例仅是应用本发明技术方案的典型范例，凡采取等同替换或者等效变换而形成的技术方案，均落在本发明要求保护的范围之内。

下面结合附图对本发明的技术方案做进一步的详细说明：

本发明基于一种基于大尺度衰落信道信息的能效优化快速天线选择算法。利用基于大尺度衰落信道信息的分簇选择算法筛选出系统能量效率最大的ns个rau簇，再结合能效逐增算法优化每个rau簇的能量效率。最后，用ns个局部最优解来逼近全局最优解，达到系统能效优化且运算复杂度较低的目的。

分布式mimo系统功耗表达式为

分布式mimo系统的下行能效表达式为：

其中，peq表示rau端上每根发射天线的发射功率，pe为n个rau簇的射频链路功耗，为定值，h是m×nl维的信道矩阵，δ²是噪声功率。

对于信道矩阵h，其与距离矢量d(d＝[d1,d2,…,dn]^t)有关。di是移动台到第i个rau的距离。由于rau内子单元间距较近，所以可近似认为用户终端上的任意子天线到同一个rau内每根子天线间的路径损耗特性参数相同。且其包含n个独立的m×l维子信道矩阵，即：

h(d)＝[h1(d1),h2(d2),…,hn(dn)](3)

其中，子信道矩阵hn(dn)是m×l维矩阵，表示为：

其中是第n个rau上第l根天线与终端上第m根天线间的信道衰落，包含小尺度快衰落、阴影衰落和路径损耗，可表示为：

其中，是第n个rau簇的第l根天线与用户终端的第m根天线间的瞬时信道信息，～n(0,1)为小尺度快衰落。βn表示第n个rau簇与终端间的大尺衰落信道信息，由阴影衰落和路径损耗构成，与rau上的天线数目l无关，并可在多个相关时隙内保持不变，可表示为：

这里，α是路径损耗指数；dn表示第n个rau单元与终端间的距离；sn表示阴影衰落。

将式(5)带入式(4)可将信道矩阵与大尺度衰落信道信息联系到一起。

本发明是建立在具有窄带平坦衰落特性，线性时不变的离散信道上，(m,n,l)分布式mimo系统的下行传输模型可以描述为：

其中，r(t,d)为m×1维的信号接收向量；p是一个nl×nl维的正定对角矩阵，表示将给定的发射功率分配到nl个发送天线上，tr(p)为总的发射功率，用pt表示；s(t)和z(t)分别表示nl×1维的发送信号向量和m×1维的零均值方差为1的加性高斯白噪声向量。h(d)是m×nl维的信道矩阵。

如图1所示，本发明主要是基于分簇选择算法和能效逐增算法提高分布式mimo系统的能量效率。图2主要是基于分簇选择算法的流程图。图3主要是基于能效逐增算法的流程图。

下面分别给出分簇选择算法和能效逐增算法的信道资源分配具体实施步骤。

1.分簇选择算法：

本发明基于大尺度衰落信道信息变换信道矩阵，再根据系统能效公式筛选出能使系统能效最大的ns个天线簇完成优化分布式mimo系统能效的初级筛选。

具体步骤如下：

步骤1，初始化参数，其中，参数包括：信道矩阵h，分布式mimo系统的rau个数n，用户接收天线m，每个rau上发射天线数l，路径损耗指数α，阴影衰落标准差sn，小区半径，n个rau簇的位置，移动台位置，迭代器i＝0，系统最大能量效率ηtemp＝0，系统能量效率最大的rau簇个数ns＝n；

步骤2，已知信道矩阵h，根据信道矩阵元素与大尺度衰落信道信息之间的关系：

将大尺度衰落信息βn按照降序排列，得到新的信道矩阵h*，矩阵可表示为：

其中，βn<βn-1<…<β1。若迭代删除h^*的最后l列，即每次删除βn最小的rau，再比较前后的系统能效，最后选择出使系统能效最大的ns个簇；

步骤3，根据分布式mimo系统的下行能效表达式计算出最初的系统能量效率η，且令ηtemp＝η；

步骤4，更新参数：迭代器更新i＝i+1，判断此时迭代器数和rau个数n的大小，如果i>n,算法退出，否则继续下一步；

步骤5，迭代删除h^*的最后l列，即每次删除βn最小的rau，再比较前后的系统能效，最后选择出使系统能效最大的ns个簇；

步骤6，返回最后得到的ns，信道矩阵h*，以及系统最大能量效率ηtemp。

2.基于能效逐增的优化算法：

在本发明中，由于在rau簇内，每增加一根天线，将信道容量的增量记为δc，且δc是不定值，即：

其中，是m×1维的信道矩阵，且由公式(15)可知，δc只与有关，若呈单调性变化，则δc也将随之呈同向的单调变化。在功率分配为平均分配的条件下，每增加一根天线的功耗增量表示为δp是定值，且δp＝peq。

假设从0根天线开始，分别用ctemp和ptemp来表示当前系统的信道容量以及功率损耗，在增加一根天线后系统信道容量增量可表示为δc，功率损耗增量可表示为δp，则能效表达式为：

综上分析可知，若信道容量的增量δc呈单调递减变化而功率损耗增量δp不变，则能效增量δηee的变化会逐步变缓，直至出现最大值点。那么，最多经过l次选择，即可得到单个簇的最优能效。由于递增算法存在局部最优而整体未必最优的缺点，为了让能效逐增算法在搜索时避免出现这样的状况，必须确保信道容量的增量δc呈单调递减排列，即要求为单调递减排列。这就需要在分簇选择后得到的信道矩阵h*的基础上重新构建新的信道矩阵hs。

可知，经过前期分簇选择后的信道矩阵h*是m×nsl维，现将矩阵h*中每个簇的列元素按元素和的大小成降序排列，得到新的矩阵hs，表示为：

其中，是m×l维矩阵，它表示第n个簇的信道矩阵，且根据元素和的大小成降序排列，最多经过l次选择，即可得到该簇下系统的最优能效。若每个被选簇的能效都得到优化，此时，可用局部最优来毕竟全局最优，则分布式mimo系统能效也会得到进一步改进。

具体步骤如下：

步骤1，初始化参数：rau簇数目迭代器n＝1,2,…,ns，每个rau上发射天线数迭代器l＝1,2,…,l，第n的rau簇的系统能效可使rau簇系统能效最优的发射天线数lnum＝0；

步骤2，重构新的信道矩阵：基于分簇选择算法得到的信道矩阵h*，将矩阵h*中每个簇的列元素按元素和的大小成降序排列，得到新的矩阵hs，且令n＝1；

步骤3，判断n与ns的大小。若n>ns，则算法退出；否则令l＝1，转下一步；

步骤4，优化每个rau簇内的能量效率。

步骤5，根据已优化的rau簇，得到可使该簇的能量效率达到最优的信道矩阵；

步骤6，判断n与ns的大小，如果n＝ns，根据步骤5得到的信道矩阵计算出系统能效，算法退出；否则令n＝n+1，重复步骤3至步骤6；

步骤7，返回最终的最优信道矩阵，以及计算出系统的最优能效。

本发明技术方案的优点主要体现在：在有效降低运算复杂度的同时，提高分布式mimo系统的能量效率，与能效最优的穷举法相比，本算法能效趋近于它，但本算法的复杂度远远低于穷举法。

此外，本发明也为同领域内的其他相关问题提供了参考，可以以此为依据进行拓展延伸，运用于移动通信技术领域内其他的技术方案中，具有很强的适用性和广阔的应用前景。

本发明尚有多种实施方式，凡采用等同变换或者等效变换而形成的所有技术方案，均落在本发明的保护范围之内。

对于本领域技术人员而言，显然本发明不限于上述示范性实施例的细节，而且在不背离本发明的精神和基本特征的情况下，能够以其他的具体形式实现本发明。因此，无论从哪一点来看，均应将实施例看作是示范性的，而且是非限制性的，本发明的范围由所附权利要求而不是上述说明限定，因此旨在将落在权利要求的等同要件的含义和范围内的所有变化囊括在本发明内，不应将权利要求中的任何附图标记视为限制所涉及的权利要求。

此外，应当理解，虽然本说明书按照实施方式加以描述，但并非每个实施方式仅包含一个独立的技术方案，说明书的这种叙述方式仅仅是为清楚起见，本领域技术人员应当将说明书作为一个整体，各实施例中的技术方案也可以经适当组合，形成本领域技术人员可以理解的其他实施方式。