基于CoMP的异构网络信道及功率资源联合分配方法与流程

本申请尤其涉及一种基于comp的异构网络信道及功率资源联合分配方法。

背景技术：

近十年来，无线通信系统的数据流量呈现爆发式增长。预计2010至2020年，全球移动数据流量将增长超过100倍。因此，下一代5g移动通信网络要求理论峰值传输速率能够达到10gb以上，比当前4g的网络传输速率(20～100mbps)高出数百倍。而传统的单层无线网络接入技术已接近理论极限，无法满足需求。因此，在同一地区实现多层网络叠加覆盖的异构网络成为5g网络的重要选择，并且网络部署将会呈现出密集化的发展趋势。

通过在传统宏小区中增加小小区(smallcell)基站、中继或分布式天线等低功率节点，异构网络缩短了基站与终端间的信号传输距离、增强了接收信号强度，进而提升了系统容量。在热点地区实现多层覆盖有效分担了网络负荷，给用户带来更好的互联网体验。但同时，为了高效利用频谱资源，宏小区和小小区通常共享同一频谱资源。因此，层间干扰是异构网络技术发展面临的瓶颈问题。

协作多点(comp)技术是lte-a演进的release11及之后版本中的一项关键技术，旨在抑制或消除小区间的干扰、提升小区边缘用户服务质量。支持comp技术的基站通过回程链路交换用户及信道状态等信息，联合调度系统资源，使得来自其他基站的同信道信号不会对用户造成严重干扰，甚至可以成为有用信号。已在传统宏小区网络中得到了充分的研究和应用，证明了其在解决小区干扰问题方面的有效性。因此，将comp引入异构网络来抑制层间干扰、提升系统性能成为异构网络领域新的研究热点。

【申请内容】

本申请实施例提供了一种基于comp的异构网络信道及功率资源联合分配方法，以实现提升系统吞吐量的同时保护用户间的公平性。

本申请基于comp的异构网络信道及功率资源联合分配方法，包括：

构建异构网络，所述异构网络中各层基站均支持comp联合传输模式；

以实现最差用户的吞吐量达到最大化为目标，建立所述异构网络的信道及功率资源分配的数学模型，所述数学模型表示为：

其中，所述数学模型的约束条件包括：确保每个基站分配给各个信道的传输功率总和不会超出该基站的最大传输功率限制，公式表示为：subjectto以及，保证每条信道最多分配给一个用户，公式表示为：

基于信道和功率资源联合分配算法，计算信道分配向量和各基站的功率分配向量

进一步地，所述异构网络由一个处于网络中央的宏基站及所述宏基站覆盖范围内的b个小基站组成，其中所述小基站类型为micro、pico和femto基站中之一或组合。

进一步地，所述信道和功率资源联合分配算法包括：

步骤301，设定迭代次数序号：t＝1，最大迭代次数tmax；设定初始功率：设定乘子μ、υ、β，步长α、λ，误差阈值ε；

步骤302，进行t次迭代，基于分配向量算法求最佳信道分配向量ρ(t)；基于多基站功率联合分配算法求最佳功率分配向量p(t)；分别更新乘子λ(t)、μ(t)、α(t)和β(t)；

步骤303，返回步骤302，直到||μ(t+1)-μ(t)||2＜ε且||β(t+1)-β(t)||2＜ε，或t＝tmax；

步骤304，输出信道分配向量ρ和功率分配向量p。

进一步地，所述分配向量算法包括：

步骤401，信道集合φ＝{1,2,...,c}；

设定初始信道分配参数用户累计速率

计算用户在各信道上可获得的传输速率

步骤402，迭代计算：找到传输速率最小的用户u^*，即找到能使用户u*得到最大传输速率的信道c^*，即令信道分配变量更新信道集合φ＝φ-{c^*}，用户速率

步骤403，返回步骤402，直到

步骤404，输出信道分配向量ρ。

进一步地，所述多基站功率联合分配算法包括：

步骤501，设定迭代次数序号：k＝1；设定初始功率分配向量p(0)为由信道和功率资源联合分配算法所获得的p(t-1)；

步骤502，第k次迭代：对所有基站b，0≤b≤b；基于求g^c和计算1/μb：对任意c，求并按降序排序；令j从c到1递减

如果则停止；

基于式其中，[·]⁺＝max(0,·)，求

步骤503，求最差用户速率k＝k+1；返回步骤502，直到rmin收敛；

步骤504，输出功率分配向量p。

以上技术方案中，以最大化最差用户吞吐量为目标建立数学模型，进而设计了基于拉格朗日对偶分解的迭代算法。在每一次迭代内，将原问题分解为4个子问题，从而降低算法的计算复杂度，并分别设计了信道分配算法以及基于迭代和基于二分法的功率分配算法。在用户吞吐量及公平性等方面要优于其它现有方法，并且迭代算法能在较少的迭代次数内实现收敛。

【附图说明】

为了更清楚地说明本申请实施例的技术方案，下面将对实施例中所需要使用的附图作简单地介绍，显而易见地，下面描述中的附图仅仅是本申请的一些实施例，对于本领域普通技术人员来讲，在不付出创造性劳动的前提下，还可以根据这些附图获得其它的附图。

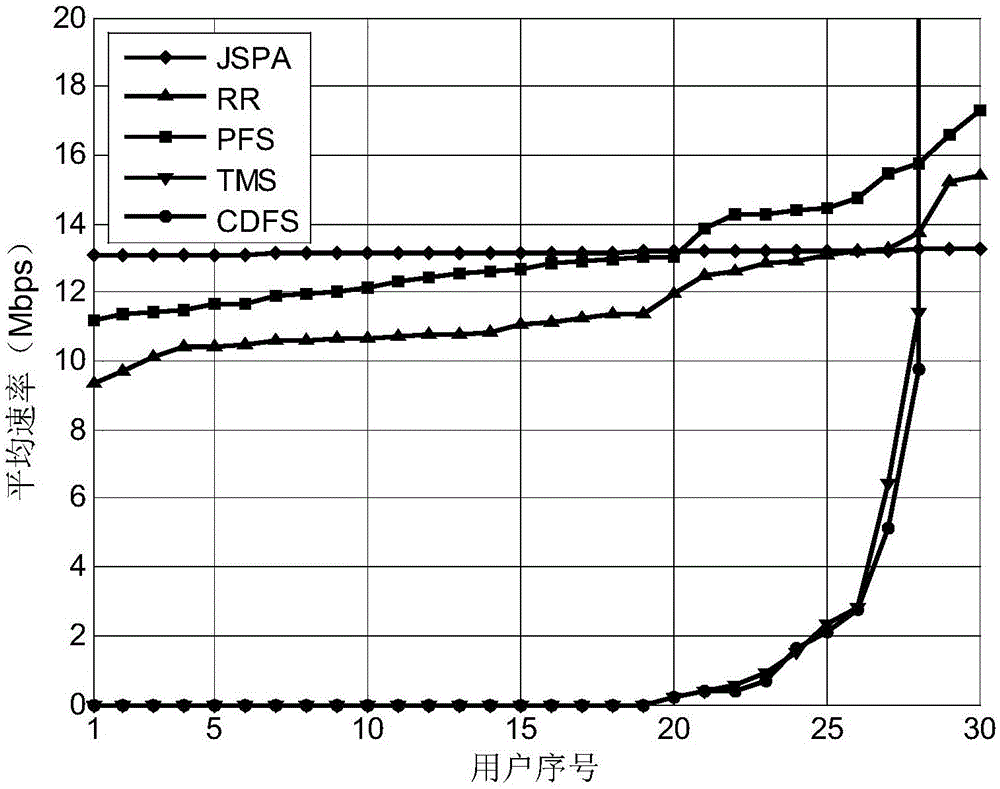
图1为本申请用户的平均速率比较；

图2为本申请用户平均速率归一化概率密度估计；

图3为本申请用户最差速率长时比较分析，u＝30；

图4为本申请不同用户密度场景下的最差用户速率；

图5为本申请不同基站密度下的用户最差速率，u＝30；

图6为本申请公平性指数比较；

图7为本申请用户信道最大调度时间间隔对比；

图8为本申请多基站功率联合分配算法的收敛性；

图9为本申请功率资源联合分配算法的收敛性；

图10为本申请信道分配和简便算法公平性指数比较；

图11为本申请于迭代的功率分配算法以及基于二分法的功率分配算法乘子收敛情况比较。

【具体实施方式】

为了更好的理解本申请的技术方案，下面结合附图对本申请实施例进行详细描述。

应当明确，所描述的实施例仅仅是本申请一部分实施例，而不是全部的实施例。基于本申请中的实施例，本领域普通技术人员在没有作出创造性劳动前提下所获得的所有其它实施例，都属于本申请保护的范围。

在本申请实施例中使用的术语是仅仅出于描述特定实施例的目的，而非旨在限制本申请。在本申请实施例和所附权利要求书中所使用的单数形式的“一种”、“所述”和“该”也旨在包括多数形式，除非上下文清楚地表示其他含义。

异构网络由一个处于网络中央的宏基站(macro基站)及其覆盖范围内的b个小基站组成。小基站可以为micro、pico和femto基站等多种类型。也就是说，本申请提出的资源分配方案适用于多层异构网络。令宏基站序号为0，各小基站序号为1≤b≤b。在联合传输模式下，宏基站及各小基站协作向u个用户提供数据传输服务。为基站b(b∈{0,1,...,b})的最大传输功率。

设系统共有c个信道，为宏基站和小基站所共享。定义信道分配变量

表示信道c(c∈{1,...,c})分配给了用户u(u∈{1,...,u})，反之为避免小区内同信道干扰，每条信道同时最多分配给一个用户。设为基站b在信道c上分配的传输功率，如果且表示基站b将在信道c上向用户u传输数据。通过本申请的资源联合分配方案可以动态地确定用户u的服务基站而不是像现有一些方案预先指定各个用户的服务基站，并在整个资源分配过程中保持不变。这种动态分配方案可以更加灵活地分配资源，提高系统频谱效率。

令表示在信道c上，从基站b到用户u的无线链路信道增益。假设各基站能够及时获得用户准确的信道状态信息(csi)。

在comp联合传输模式下，用户u从各协作基站接收信号，在信道c上获得的信噪比(snr)可表示为

其中，n0为加性高斯白噪声功率。在信道c上，用户u可获得的最大传输速率为：

其中，δf为信道带宽。因此，在一次资源调度中，用户u可以获得的最大吞吐量可表示为：

本申请通过确定最佳的信道分配向量和各基站的功率分配向量使最差用户的吞吐量达到最大化，从而在提升系统吞吐量的同时保护用户间的公平性。

本申请基于comp的异构网络信道及功率资源联合分配方法一较佳实施例，包括：

构建异构网络，所述异构网络中各层基站均支持comp联合传输模式；

以实现最差用户的吞吐量达到最大化为目标，建立了如下数学模型：

其中，约束条件(4a)确保每个基站分配给各个信道的传输功率总和不会超出该基站的最大传输功率限制，约束条件(4c)保证每条信道最多分配给一个用户。

本申请，首先在目标函数中引入一个新的变量来简化目标函数，同时将信道分配变量的0-1约束松弛为区间[0,1]，将(4)等价改写为

改写后的问题(7)虽然已简化为单一的最大化问题，但同时存在着整数变量(信道分配变量)和非整数变量(功率分配变量)，仍然是计算复杂度非常高的非线性混合整数规划问题。

为找到一种快速收敛的算法，本申请首先采用拉格朗日对偶分解法来松弛约束条件，降低问题复杂度。对式(7)，列出其拉格朗日式子：

其中，μ＝{μ0,...,μb}、υ＝{υ1,...,υc}和β＝{β1,...,βu}是分别对应于约束条件(7a)、(7c)和(7e)的拉格朗日乘子。至此，拉格朗日对偶函数可表述为

通过对偶分解，可以在给定的μ、υ和β下最大化求得原问题的最佳资源分配解。通过拉格朗日对偶法，问题(9)相比问题(7)减少了约束条件，但问题(9)的求解需要同时确定资源分配向量及拉格朗日乘子，仍然具有较高的计算复杂度。

为此，本申请进一步将原资源联合分配问题分解为4个子问题：信道分配、功率分配、的选择及乘子更新。采用迭代法分别求解子问题，直到算法收敛。

详细步骤见算法1：信道和功率资源联合分配算法。

算法1：信道和功率资源联合分配算法

步骤101，初始化：

设定迭代次数序号：t＝1，最大迭代次数tmax。

设定初始功率：

设定乘子μ、υ、β，步长α、λ，误差阈值ε。

步骤102，第t次迭代：

基于信道分配算法(算法2)求最佳信道分配向量ρ(t)。

算法3：多基站功率联合分配算法

基于多基站功率联合分配算法(算法3)求最佳功率分配向量p(t)。

分别更新乘子λ(t)、μ(t)、α(t)和β(t)。

步骤103，返回步骤102，直到||μ(t+1)-μ(t)||2＜ε且||β(t+1)-β(t)||2＜ε，或t＝tmax。

步骤104，输出信道分配向量ρ和功率分配向量p。

令表示功率分配向量已知情况下的信道分配向量的局部最优解。根据最优解的kkt条件，可以得到以下关系式：

为信道分配向量，只有0、1两种取值。当时，有

即当时，有

即综合这两种情况可以得到表达式

其中，

由于信道分配变量的约束条件(4c)在式(8)中被松弛，因此式(13)获得的信道分配方案不能保证每条信道最多只分配给一个用户。因此，一些基于拉格朗日算法的文献采用h最大值作为信道分配方法[]，但这样并不能保证获得局部最优解。为此，本申请基于maxmin思想，设计了信道分配算法(见算法2)。

如算法1的步骤102所示，在第t次迭代中，算法2：信道分配算法，将基于上一次迭代获得的最佳功率分配向量p(t-1)，计算出当前信道分配的局部最优解。核心思想是：将最好的信道(用户在此信道上可以获得的数据传输速率最大)分配给累计速率最小的用户，直到所有信道分配完毕。

算法2：信道分配算法

步骤201，初始化：

信道集合φ＝{1,2,...,c}。

设定初始信道分配参数用户累计速率

计算用户在各信道上可获得的传输速率

步骤202，迭代：

找到传输速率最小的用户u^*，即

找到能使用户u^*得到最大传输速率的信道c^*，即

令信道分配变量

更新信道集合φ＝φ-{c^*}，用户速率

步骤203，返回步骤202，直到

步骤204，输出信道分配向量ρ。

令为信道分配向量ρ已知情况下的功率分配向量局部最优解，根据最优解的kkt条件，可以得到以下关系式：

基于算法2，本申请已知任一信道c已分配给了用户uc，因此可将(15)简化为

当时，有

即

结合的情况，并令和可以将功率分配变量表达为：

其中，[·]⁺＝max(0,·)。

虽然式(19)与注水法的解有相似的形式，但中包含的是其他协作基站的功率分配变量，需要和一同确定。所以，式(19)不能直接求出所有基站的功率分配解。为此，本节提出了基于迭代的多基站功率联合分配算法(算法3)。该算法基于算法1中前次迭代获得的最佳功率分配向量p(t-1)和拉格朗日乘子β(t-1)，求当前的功率分配向量p(t)的局部最优解。基本思路是：在第k次迭代中，固定其他基站的功率分配值，依次计算每个基站b的水位线1/μb，并根据式(19)求出该基站的当前功率分配向量基于当前功率分配向量p(k)，更新最差用户速率并进入下一次迭代，直到算法收敛。

算法3：多基站功率联合分配算法

步骤301，初始化：

设定迭代次数序号：k＝1。

设定初始功率分配向量p(0)为由算法1所获得的p(t-1)。

步骤302，第k次迭代：

对所有基站b，0≤b≤b

基于求g^c和

计算1/μb：

对任意c，求并按降序排序。

令j从c到1递减

如果则停止。

基于式(19)，求

步骤302，求最差用户速率

返回步骤302，直到rmin收敛。

步骤304，输出功率分配向量p。

算法1：信道和功率资源联合分配算法由基站的资源管理器运算。若为lte系统，基站资源管理器每个tti(1ms时长)开始时执行该算法。基站调入用户在上个tti上报的信道条件并设定算法需要的一些参数μ、υ、β，α、λ、ε的初始值，运行算法1，得到信道分配向量ρ、p，此为最终输出结果。无线资源(基站的信道资源和功率资源)分配就是确定这两个参数，基站知道这两个参数就知道在这个tti中哪个信道分给哪个用户，也就是传哪个用户的数据，采用多大的功率来传输。

算法1：信道和功率资源联合分配算法可以实现公平的资源分配(通过maxmin最大化最差用户速率目标)，各用户得到的传输速率很近。这个在图1中可以明显看出来，用户速率最接近。无线资源分配算法一个角度是运营商希望总体吞吐量大，另一个角度是用户希望公平。但信道和功率资源是有限的，两个角度有冲突。但我们的算法目标是最大化最差，能够兼顾公平和系统吞吐量。图1说明了用户公平性，图2用户中心速率最高，且很集中，说明用户整体速率都偏高，系统总体吞吐量比较好

算法1中调用算法2求信道分配向量ρ(t)，调用算法3求最佳功率分配向量p(t)，在算法1中不断更新这两个向量，直到最后收敛于最终的ρ、p，就是输出值。在基站中资源分配要非常快速(ms级)。本申请最终调用的是推导的结果，还有推导采用的大问题分解方法，使得算法很简单，这样对于计算能力有限的基站来说是好的，不需要大的内存和功率，图8到图11说明了本申请算法几次迭代就能收敛，也就是算法1只要调用算法2和3几次就能输出最终值了。如果用matlab这些工具来解maxmin的优化问题，一天也跑不出来一个结果的。

拓展实施例，算法4是替换算法3的另一种功率分配算法。在无线网络资源分配中，二分法也常被用来计算功率分配问题。采用二分法求解功率分配子问题，示于算法4。通过分析算法流程，可看出算法3和算法4的主要区别在于乘子μ的更新方式不同。算法3先将μ可能的取值按降序排列，然后选择合适的水位线，也就是合适的μ值，再根据式(19)计算出功率分配解。而算法4先通过二分法获得μ值，再根据式(19)更新功率分配解，最后根据约束条件更新μ的上下限，用于下一次迭代中μ值的计算。对于μ的上下限，不同的初始值设定在很大程度上会影响到算法4的收敛速度，而算法3的最大迭代次数上限即为子信道数目c，因此，基于二分法的算法4具有更大的不确定性。

算法4：基于二分法的功率分配算法

步骤401，初始化：

设定迭代次数序号l＝1，设定误差阈值ε。

设定初始功率分配向量p(0)为由算法4-1所获得的p(t-1)。

步骤402，第l次迭代：

设定乘子μ的上限μ^max和下限μ^min。

对所有基站b，0≤b≤b

当时执行以下操作：

基于公式(19)，求

若则更新否则更新

步骤403，求最差用户速率

返回步骤402，直到rmin收敛。

步骤404，输出功率分配向量p。

在求解信道分配子问题和功率分配子问题之后，本申请可以对(9)所示的拉格朗日对偶函数进行简化，使目标函数和约束条件中只留下与相关的部分，并将其重新表示为：

令为问题(20)的最优解。要求目标函数的最大值，可以分两种情况进行讨论。当时，考虑到是非负数，要使的值最大，应等于0；当时，应取其范围内的最大值，即结合这两种情况，并令可以得到的最优选择方案：

根据式(13)和(19)，要完成信道分配和功率分配，需要知道拉格朗日乘子μ、υ和β的值。

采用了次梯度法来对乘子的值进行更新。首先，将问题(9)的对偶问题表示为

mind(μ,υ,β)(23)

subjecttoμ≥0,υ≥0,β≥0

进而可以得到d(μ,υ,β)的次梯度表达式：

由于每条信道最终都会分配给某个用户，并且在一次资源调度内最多只能分配给一个用户，即对任意信道c(c∈{1,...,c})始终成立。因此，恒成立，只需要对μ和β做乘子更新。更新方法如下：

μb(t+1)＝[μb(t)-λ(t)δμb(t)]⁺(25a)

βu(t+1)＝[βu(t)-α(t)δβu(t)]⁺(25b)

其中，λ(t)和α(t)分别是乘子μ和β的更新步长。

本申请在基于lte的异构网络下行链路对提出的方案和算法的性能进行验证。子信道数目c＝50，子信道带宽δf＝180khz，宏基站的最大传输功率大尺度衰落的计算遵循l＝122.85+34.88log10(d)，其中d表示基站到用户的距离，单位是km。小尺度衰落模型为归一化的瑞利衰落，噪声功率密度为-174dbm/hz。此外，服从对数正态分布的阴影衰落的均方差为10db，穿透损耗为20db。在宏小区的覆盖范围内均匀分布6个用户和12个流量热点区域，每个热点区均匀分布2个用户。

为验证本申请提出的信道和功率资源联合分配方案(此处简写为jspa)，本申请将其与另外四种典型的异构网络资源分配方案进行了仿真对比。这四种参考方案分别为：①经典的轮询方案(rr)，每条信道按序号依次分配给每个用户，各基站的传输功率在所有信道上平均分配；②以最大化系统吞吐量为目标的信道和功率联合资源分配方案；③基于累计分布函数的调度方案(cdfs)，根据用户速率的累积分布函数进行信道分配，基站传输功率在所有信道上平均分配；④比例公平调度方案(pfs)，兼顾了系统吞吐量以及用户之间公平性的资源分配方案。

本申请将在macro-femto异构网络场景下对这几种方案进行了比较分析。femto基站最大传输功率

图1为测得的各用户在50个tti内获得的平均传输速率。将用户按照各自的平均速率升序排列。从结果可以看出，本申请提出的jspa算法所获得的各用户平均速率非常相近，rr和pfs获得的最高和最低平均速率之间呈现出一定的差距，大致相差6mbps左右。而tms和cdfs两种方案下，虽然用户最高平均速率值远大于20mbps，有部分用户却未能获得资源(平均速率接近0mbps)，用户之间的速率差距非常明显。

图2中给出了不同方案下用户平均速率的归一化概率密度估计图，从另一个角度对结果进行了分析。首先，从图中可以看到，tms和cdfs两种方案的平均速率分布范围最广(图中只表示出了0-20mbps的很小一部分)，其次是rr和pfs。jspa方案得到的平均速率分布范围最小，表示用户获得的平均速率大小最为接近。另一方面，从图中也可以观察概率密度最大的点所对应的平均速率大小，也就是大多数用户可以获得的平均速率，简称为集中速率。可以看到，tms和cdfs中绝大部分用户的平均速率都是0mbps。rr和pfs的集中速率分别为11mbps和12mbps左右，相对较高，但仍低于jspa方案的13mbps。图1和图2说明jspa方案得到的用户平均速率分布范围是最为集中，也就是各用户之间的平均速率差别最小，而且方案jspa得到集中速率值最大。说明本申请提出的jspa方案可以实现用户吞吐量和公平性之间的平衡。

接下来观察用户最差速率在长时调度过程中的变化情况，设定用户数为30，结果如图3表示。可以看到，在整个资源分配的过程中，tms和cdfs的最差平均速率始终是0mbps，rr和pfs的最差平均速率出现上下浮动，但总的来说rr的最差平均速率要高于pfs。而jspa方案得到的最差平均速率则呈现出随tti递增的趋势，而且始终高于另外四种方案。由此可以得出以下结论：在长时调度过程中，相比于其他四种参考方案，本申请提出的jspa方案可以得到最大的最差平均速率，实现了方案设定的目标。

为了充分验证jspa方案的性能，本小节设定了不同用户密度、不同基站密度的多种仿真场景以模拟现实中的各种情况。对比了各种场景下各方案获得的最差用户平均速率，结果示于图4和图5。图中每个点均为各用户在50个tti内获得的速率平均值。从图中可以看出，tms和cdfs的最差平均速率在任何场景下都是0mbps。jspa、rr和pfs的最差平均速率都随着用户数目的增多呈现出下降的趋势，因为随着用户的增加，各用户获得的信道数减少。但是无论是在用户数目少于信道数目还是在相反场景下，jspa得到的最差平均速率始终大于其他四种方案。从图5可以看出，jspa、rr和pfs三种方案的最差平均速率都随着小基站数目的增多而逐渐变大，并且jspa的最差速率始终高于其他方案。总而言之，相比于其他四种方案，jspa方案在各种场景下均能使最差用户平均速率实现最大化。

为直观衡量方案的公平性，本申请计算了长时调度中用户速率的公平性指数：

其中，ru表示当前tti内用户u的平均速率，公平性指数j的值越大，表示用户平均速率之间的公平性越高。图6所示为用户平均速率的公平性指数随tti变化的情况。在三种考虑了公平性的资源分配方案中，jspa相比rr和pfs一直能够获得更高的公平性指数。而且jspa的公平性指数是随tti递增的，在大约4个tti后就收敛到了最大值1。换句话说，jspa能在较短的调度时间内实现用户速率的公平性。

此外，还观测了最差用户的最大调度间隔(mit)。调度间隔即为用户前后两次分配到资源的间隔时长。在50个tti内计算每个用户的最大调度间隔，进而取出最差用户的调度间隔值，即为mit。图7对比了三种场景下不同方案的mit值。由于rr方案的分配原则是将信道按序依次分配给每个用户，所以它的调度间隔最小。本申请提出的jspa方案可以获得与rr方案非常接近的调度间隔值，优于其它三种方案。因为调度间隔可以反映用户获得服务的时间延迟，以上结果证明了所提出的jspa方案可以使用户获得较稳定的网络连接服务，适用于对延迟和延迟抖动要求较高的应用，如视频流传输。

在仿真过程中，还验证了本申请提出的算法的性能。图8图9是多基站功率联合分配算法(算法3)和基于拉格朗日对偶分解的迭代信道及功率资源联合分配算法(算法1)的最差用户速率随迭代次数的变化情况。分别在四种异构网络场景下进行观测。仿真结果表明了，算法3和算法1都能在较少的迭代次数内实现收敛。

图10将本申请所提出的信道分配算法2与基于拉格朗日推导后的简便算法进行对比，可以看到，提出的信道分配算法能在较短的资源分配时间内达到更高的公平性指数，更好地实现用户之间的公平性。

图11针对所提出的基于迭代的功率分配算法(算法3)以及基于二分法的功率分配算法(算法4)，对比了两种算法下乘子μ的收敛情况。可以看到，算法3在大约8次迭代后就实现了收敛，而算法4的情况比较复杂。一方面，无论μ的初始上限μ^max的取值是多少，即使是在最好的情况下，算法4也需要至少12次迭代之后才会收敛。另一方面，如果μ^max的值不同，算法4达到收敛需要的迭代次数也会呈现出很大的不同，其收敛性有着很大的不确定性。

以上所述仅为本申请的较佳实施例而已，并不用以限制本申请，凡在本申请的精神和原则之内，所做的任何修改、等同替换、改进等，均应包含在本申请保护的范围之内。