基于OB-MMSE检测算法的光广义空间调制方法与流程

本发明是将光广义空间调制技术与ob-mmse信号检测算法相结合，构建了一种基于ob-mmse检测算法的光广义空间调制方案，属于无线光通信技术领域。

背景技术：

传统光空间调制(osm)因为每时隙只激活一个激光器发送信息，导致其频谱效率较低，同时要求其激光器数目必须是2的整数次幂。为了弥补这些缺陷，研究者提出了广义空间调制(gsm)。gsm是在sm的基础上，通过每次激活多根(大于等于2)天线来发送信息，激活的多个天线上可传输相同或不同的信息。因此，gsm技术有效地克服了发射天线数必须是2的整数次幂的限制，同时它还结合了sm和空间复用的优势，进一步提高了系统的频谱效率。因此，近年来在无线通信领域掀起了研究热潮。

基于gsm技术的这些优势，研究者将gsm技术引入到光通信中，结合脉冲幅度调制(pam)，提出了一种适用于室内可见光通信(vlc)的光广义空间调制(ogsm)。与传统的osm相比，ogsm有效的降低了osm系统的误比特率，尤其是在强相关信道中。然而对于室外大气信道而言，由于大气湍流、大气衰减等因素的影响，使得大气信道具有更强的时变性和随机性。因此，研究基于大气信道的ogsm技术显得非常迫切。另外，由于ogsm信号同时包含了激活激光器的位置组合和数字调制符号，接收端需要估计出发送激光器的组合和所发送的调制符号，因此接收端信号的检测是一个关键。而在一般的ogsm中，通常采用ml检测算法，它虽然获得了最优的误码性能，但高的复杂度限制了其在实际中的应用。针对这一问题，有研究者采用符号搜索树的方法，研究了ogsm调制的译码算法。该方法虽然获得了最优的ogsm符号子集，但由于采用树形搜索方法，其复杂性也相对较高，因而只适合于一些简单的应用场景。因此，寻找并获得低复杂度的信号检测算法是ogsm技术走上实用化的关键。

由此可见，如何获得误码性能优良、译码复杂度低、实用性强的译码算法是光广义空间调制技术走上实用化的关键。

技术实现要素：

本发明的目的是提供一种基于ob-mmse检测算法的光广义空间调制方法。

本发明是基于ob-mmse检测算法的光广义空间调制方法，其步骤为：

步骤1：发射端利用激光器映射向量和l-ppm调制符号的特点构建了发射信号矩阵：xl,s＝xsxl；式中，xl＝[…,0,…,1,0,1,…]^t是一个nt×1维的激光器映射向量，且非零元的位置表示激活激光器的索引号；(1≤r≤l表示发送脉冲的位置)是一个1×l维的脉冲映射向量；其中，nt、l分别表示激光器数目和l-ppm调制的阶数；

步骤2：在接收端引入ob-mmse信号检测方法，并依据ogsm调制信号的特点对其权值进行了修正，提出了一种适合于光广义空间调制的ob-mmse信号检测算法，推导了对数正态湍流信道中阈值的选取方法；其分步骤如下：

步骤2.1：计算信道矩阵h每一列hj的伪逆与接收向量y的乘积：

其中，j＝1,2,…,nt；则是一个nt×l维的矩阵；

步骤2.2：计算m组所有可能的激光器组合的权重wk,并按其权值大小进行可靠性排序；

其中，k＝1,2,…,m；将所得的m组权值w＝[w1,w2,…,wm]^t由大到小依次进行排序，得到[k1,k2,…,km]＝argsort(w)；其中，k1,k2,…,km是对应于权重大小的激活激光器的组合；

步骤2.3：按照排好后的权值顺序依次采用mmse算法进行信号检测；即

步骤2.4：引入一个阈值vth，并利用该阈值对(4)式所得结果进行可靠性判断，即：

如果(4)式成立，则

如果输出不满足(4)式，则进行下一组激光器组合的判断；

当计算次数j＞m时依然不满足该条件，则采用ml检测来估计激活激光器的序号和脉冲位置，即：

其中，为所有可用的激光器组合和l-ppm脉冲位置集合；步骤2.5：阈值的选取；假设xs,l＝xlxs和分别为实际发送的符号和估计出的符号；当时，是一个自由度为nrl的中心卡方随机变量；而当时，是一个非中心卡方随机变量；其阈值可选取为：vth＝anrln0；其中，a为一常数，n＝nrl为自由度。

本发明的益处在于：所构建的光广义空间调制方案有效地提高了系统的频谱效率。与ml算法相比，提出的ob-mmse算法在牺牲较小误码性能的情况下，有效降低了ml算法的复杂度。与经典的mmse算法相比，虽然所提算法的复杂度略有增大，但其有效地降低了误码率，而且还适用于接收机数目少于发射机数目的系统。

附图说明

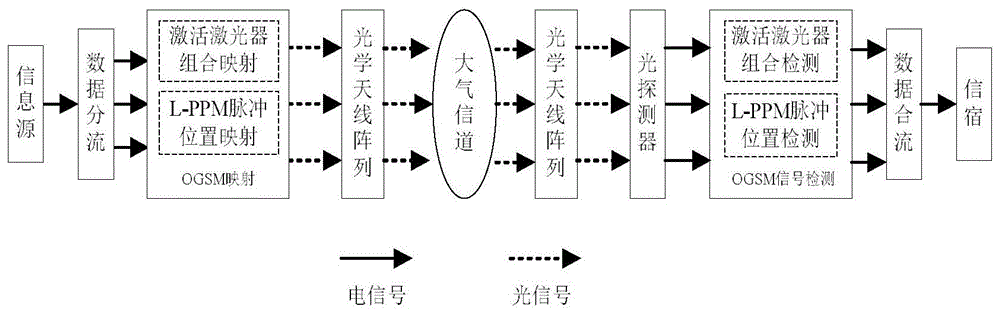
图1为gosm系统框图，图2为ob-mmse算法的流程图，图3为n和a取不同值时的p(ρ≤vth)，图4为a取不同取值时ob-mmse算法的误码性能，图5为ml、mmse和ob-mmse三种算法的误码性能，图6为不同系统中三种算法的误码性能，图7为mmse算法和ob-mmse算法的相对复杂度，图8为a取不同值时ob-mmse算法的相对复杂度。

具体实施方式

本发明是基于ob-mmse检测算法的光广义空间调制方法，其步骤为：

步骤1：发射端利用激光器映射向量和l-ppm调制符号的特点构建了发射信号矩阵：xl,s＝xsxl；式中，xl＝[…,0,…,1,0,1,…]^t是一个nt×1维的激光器映射向量，且非零元的位置表示激活激光器的索引号；(1≤r≤l表示发送脉冲的位置)是一个1×l维的脉冲映射向量；其中，nt、l分别表示激光器数目和l-ppm调制的阶数；

步骤2：在接收端引入ob-mmse信号检测方法，并依据ogsm调制信号的特点对其权值进行了修正，提出了一种适合于光广义空间调制的ob-mmse信号检测算法，推导了对数正态湍流信道中阈值的选取方法；其分步骤如下：

步骤2.1：计算信道矩阵h每一列hj的伪逆与接收向量y的乘积：

其中，j＝1,2,…,nt。则是一个nt×l维的矩阵；

步骤2.2：计算m组所有可能的激光器组合的权重wk,并按其权值大小进行可靠性排序；

其中，k＝1,2,…,m；将所得的m组权值w＝[w1,w2,…,wm]^t由大到小依次进行排序，得到[k1,k2,…,km]＝argsort(w)；其中，k1,k2,…,km是对应于权重大小的激活激光器的组合；

步骤2.3：按照排好后的权值顺序依次采用mmse算法进行信号检测。即

步骤2.4：引入一个阈值vth，并利用该阈值对(4)式所得结果进行可靠性判断，即：

如果(5)式成立，则

如果输出不满足(5)式，则进行下一组激光器组合的判断；

当计算次数j＞m时依然不满足该条件，则采用ml检测来估计激活激光器的序号和脉冲位置，即：

其中，为所有可用的激光器组合和l-ppm脉冲位置集合；步骤2.5：阈值的选取；假设xs,l＝xlxs和分别为实际发送的符号和估计出的符号；当时，是一个自由度为nrl的中心卡方随机变量；而当时，是一个非中心卡方随机变量；其阈值可选取为：vth＝anrln0；其中，a为一常数，n＝nrl为自由度。

下面结合附图，进一步展开本发明。

本发明为一种基于ob-mmse信号检测的光广义空间调制方案，其目的是根据ogsm信号的特点，引入ob-mmse准则，提出一种适合于ogsm的ob-mmse信号检测算法，从而降低检测算法的复杂度。

如图1所示是一个有nt个激光器(ld)、nr个探测器(pd)、每时隙激活激光器数目为nt的ogsm系统。从nt个激光器中激活nt个的组合数有种，但由于所使用的激光器组合数必须为2的整数次幂，所以只需从种组合中选取其中的种即可。

其中，表示向下取整运算。设本发明采用l-ppm脉冲调制，且每时隙激活的nt个激光器均发送相同的脉冲信息。首先，发送端将原始数据比特进行串/并变换，并将其分别映射为激活激光器的索引号和l-ppm调制符号，由激活的多个激光器并经光学天线发送出去。该信号经过湍流信道传输后到达接收端，接收端需要从受到信道衰减和噪声干扰的接收信号中恢复出原始的发送信息。本发明中接收端引入ob-mmse信号检测方法，并依据ogsm调制信号的特点对其权值进行了修正，提出了一种适合于ogsm的ob-mmse信号检测算法，推导了对数正态湍流信道中阈值的选取方法。检测后的信号再经逆映射后恢复为原始信息比特。

在发射端，首先进行ogsm信号的映射，具体包括如下步骤：

步骤1：系统首先将输入的二进制信息比特流b经串/并变换划分成长为m1和m2(m＝m1+m2)两部分。其中，比特表示映射为激活激光器的序号，激光器序号的映射关系可以用一个nt×1维的向量xl来表示，即：

xl＝[…,0,…,1,0,1,…]^t(1)

其中，非零元的位置表示激活激光器的索引号，[·]^t表示转置运算。m2＝log2l比特表示映射为激活激光器上发送的l-ppm调制符号。脉冲位置调制符号的映射关系可以表示为一个1×l维的向量xs，即：

其中，1≤r≤l表示发送脉冲的位置，am表示脉冲幅度；

步骤2：经比特映射后的调制符号将会由激活的nt个激光器经光学天线后发送出去，则发射信号可表示为：

xl,s＝xsxl(3)

步骤3：当信号经大气信道传播后，接收端探测器收到的信号可表示为：

y＝ηhxsxl+n＝ηhxl,s+n(4)

式中，η为光电转换效率，n是服从均值为0、方差为n0的加性高斯白噪声，h为nr×nt维的信道衰减矩阵。在弱湍流条件下，h中的元素hij均服从对数正态分布。由于ogsm中激活激光器索引号和l-ppm符号都携带了部分比特信息，因此，发射信号xl,s的维度扩展为nt×l维，噪声n和接收信号y的维度为nr×l。

在接收端，需要从受到信道衰落和噪声干扰的接收信号中估计出原始发送信息。本发明引入ob-mmse准则，并结合ogsm信号的特点对其进行修正，构建适合于ogsm的ob-mmse信号检测算法。同时，推导出了对数正态信道下ob-mmse算法的阈值。其具体过程如下步骤：

步骤1：计算信道矩阵h每一列hj的伪逆与接收向量y的乘积：

其中，j＝1,2,…,nt。由于y是一个nr×l维的矩阵，因此，是一个nt×l维的矩阵；

步骤2：为了提高算法的可靠性，计算m组所有可能的激光器组合的权重wk,并按其权值大小进行可靠性排序。由于本发明采用l-ppm调制，扩展了发射信号和接收信号的维度，导致z为一个nt×l维的矩阵。因此，计算每组激光器组合的权值时不能只进行简单的求和运算。为此，引入f-范数来计算每组激光器组合的权值，即：

其中，k＝1,2,…,m；

步骤3：将所得的m组权值w＝[w1,w2,…,wm]^t由大到小依次进行排序：

[k1,k2,…,km]＝argsort(w)(7)

其中，k1,k2,…,km是对应于权重大小的激活激光器的组合；

步骤4：按照排好后的权值顺序依次采用mmse算法进行信号检测。即：

此时，单位矩阵en的维度为nt×nt；

步骤5：为了减小步骤4计算m组激光器组合的复杂度，引入一个阈值vth，并利用该阈值对步骤4所得结果进行可靠性判断，即：

步骤6：如果(9)式成立，则如果输出不满足(9)式，则进行下一组激光器组合的判断。当计算次数j＞m时依然不满足该条件，则采用ml检测来估计激活激光器的序号和脉冲位置，即：

其中，表示所有可用的激光器组合和l-ppm脉冲位置集合；

步骤7：对步骤5、6输出结果进行逆映射，即可恢复出原始的发射信息比特；

步骤8：阈值的选取。假设xs,l＝xlxs和分别为实际发送的符号和估计出的符号。当时，是一个自由度为nrl的中心卡方随机变量；而当时，是一个非中心卡方随机变量。因此，其阈值可选取为：

vth＝anrln0(11)

其中，a为一常数，n＝nrl为自由度。

为了更好地描述所提出算法的性能，分别仿真分析了其误码性能和计算复杂度，结果如图3～图8所示。仿真条件为：系统总功率不变，接收端已知完整的信道状态信息，闪烁因子光电转换效率η＝0.8，激活激光器数nt＝2，采用4-ppm调制方式。

图4所示为本发明在a取不同值时ogsm系统的误码性能。由图可见：随着a值的减小，该算法的误码率也逐渐减小。当a值趋于0时，该算法近似退化为ml算法。因此，阈值的选取非常关键，可根据实际需求在综合考虑误码率和复杂度的基础之上，给出合理的折中。

图5所示为本发明所提算法、ml和mmse三种不同算法的误码性能。可以发现，ml算法的误码性能最好，ob-mmse算法的性能次之，mmse算法的性能最差。

图6所示为三种检测算法在10×8、10×12两种不同系统中的误码性能。可以发现，当接收机数目大于发射机数目时，虽然mmse算法的误码性能有了明显提升，但与ob-mmse算法相比，其性能还有一定的差距。因此，本发明所提算法不仅可以获得较好的误码性能，并且还克服了mmse算法仅适用于接收机数目大于发射机数目的系统。

对检测算法而言，其复杂度是衡量该算法投入实际应用的关键性因素。因此，以一次乘法和加法运算为一个计算单位，计算了本发明所提算法的计算复杂度。本发明中所提算法的复杂度为：

式中，γ0表示计算(12)式的平均次数。ml算法、zf和mmse算法的复杂度分别为：

cml＝ml(2ntnrl+2nrl-1)(13)

为进一步说明新算法的优势，用相对复杂度r来表示其它算法相对于ml算法复杂度的降低程度，即：

复杂度对比如图7所示。可以发现：随着接收机数目的增多，两种算法的相对复杂度均增大。但ob-mmse检测算法的相对复杂度小于mmse算法的相对复杂度，这说明ob-mmse算法的复杂度明显高于mmse算法的复杂度。与mmse算法相比，本文所提的ob-mmse算法的复杂度虽然有所增大，但却换来了误码性能的改善。因此，ob-mmse算法在牺牲较少计算复杂度的条件下，极大地改善了系统的误码性能。

图8给出了a取不同值时ob-mmse算法的相对复杂度。由图可见：随着a值的变小，其相对复杂度也逐渐变小，即ob-mmse算法的复杂度逐渐增加。当a＝0时，虽然ob-mmse算法近似退化为了ml算法，但在进行信号检测之前，已经对所有激光器组合进行了可靠性排序，因此公式(10)中采用ml检测时，其所有可能的发射信号组合实际只有m种，而直接利用ml算法时，其所有的发射信号组合有m·l种。因此，当a＝0时，其译码复杂度仍比常规的ml检测低得多。

通过以上实施方式的描述，所属领域的技术人员可以清楚地了解到本发明可以用软件和硬件相结合的方式来实现。基于以上理解，本发明的技术方案对现有技术的贡献部分可以通过软件和特定硬件来执行本发明实施例所述的方法。