基于压缩感知与熵的多天线宽带频谱检测方法与流程

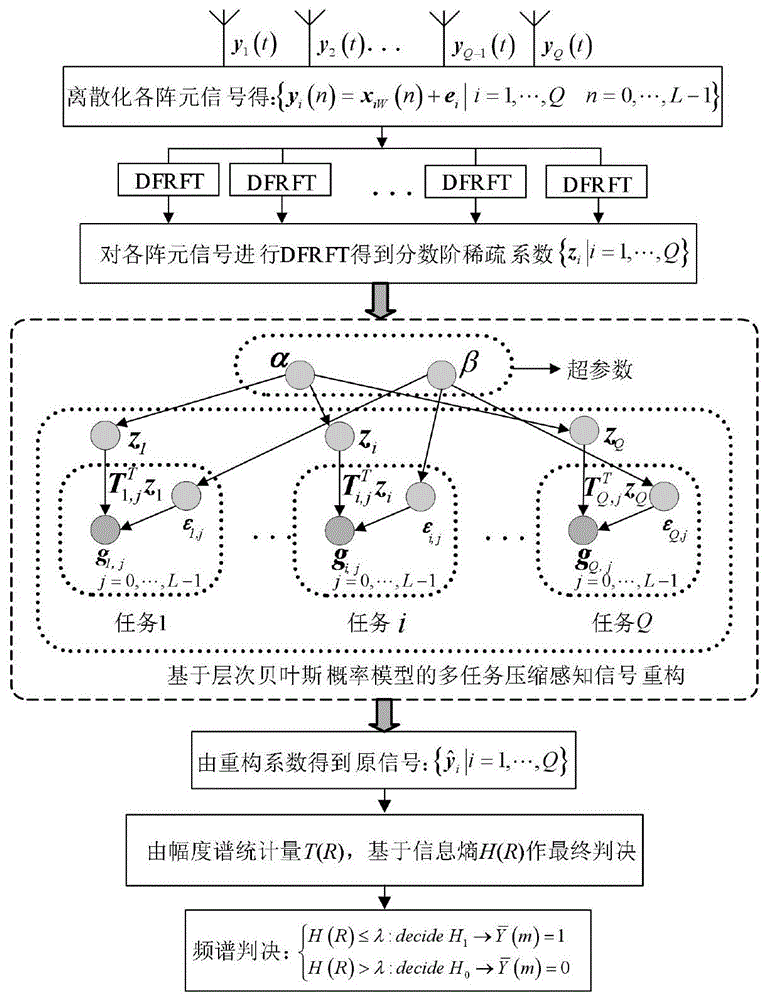
本发明属于认知无线电领域，具体涉及一种基于压缩感知与熵的多天线宽带频谱检测方法。

背景技术：

为适应未来电子战发展的新形态、新思想，形成实时、准确、有效对抗未来战场上智能化电子战设备的能力，以及在未来的复杂电磁环境中掌握制电磁权，则进一步探索和研究智能化认知电子战技术显得尤为重要。认知无线电(cognitiveradio，cr)是一种智能无线电技术，其节点通过实时频谱感知，可检测出用于通信的不含干扰频段，以实现信息安全和可靠传输。众多频谱检测算法中，能量检测(energydetection，ed)算法因其实现简单、成本低，故应用较为广泛，但ed算法是利用信号统计量进行频谱判决，与信号功率相关，则其易受噪声不确定性影响。基于此，y.ye等人提出一种改进型的能量检测(improvedenergydetection，ied)算法，可以有效提高系统噪声鲁棒性，但其主要针对拉普拉斯型噪声，则其泛化能力较弱。

近年来，为提高频谱利用率，用于宽带频谱检测的压缩感知理论已成为研究的热点方向之一。基于压缩感知理论，j.zhao等人提出一种宽带频谱检测算法(compressivesensingspectrumdetection,cssd)，其将信号映射为变换域稀疏信号，并基于优化理论实现信号重构，故具有快速高效的宽带频谱检测性能。此外，abdel-sayed等人提出一种快速匹配追踪(fastmatchpursuit，fmp)信号重构算法，利用快速准确的压缩感知贪心重构算法，可有效降低计算复杂度，但由于其对测量不确定性敏感，故信号重构精度较低。为此，y.arjoune等人提出一种基于贝叶斯压缩感知的频谱感知(bayesiancompressivesensing，bcs)算法，通过考虑给稀疏信号和测量噪声设置层次先验，减小了由测量不确定性带来的重构误差，可实现更加精确的重构。然而，在信道环境非理想场景下，bcs算法存在单节点感知失效的问题。针对此问题，y.xu等人提出一种基于贝叶斯压缩感知的多节点协作频谱感知算法(bayesiancompressivesensingbasedcooperativespectrumsensing，bcs-css)，其提高了频谱检测精度，但其数据融合过程较复杂，且将感知信息发送至数据融合中心，带来了额外的通信代价。为提高单节点频谱检测精度，刘畅等人提出一种多天线频谱感知(multi-antennaspectrumsensing，mass)算法，该算法可有效利用空域信息，提高单节点检测性能，但其未考虑信号频域的稀疏性，且未充分挖掘阵元信号之间的相关信息，从而导致算法计算效率较低。

技术实现要素：

针对上述问题，本发明提出一种基于压缩感知与熵的多天线宽带频谱检测(compressedsensingandmulti-antennabasedwidebandspectrumdetection,csma-wsd)方法。该方法一方面可以提高单节点检测能力，解决测量不确定性，提高信号重构精度，另一方面解决了噪声不确定的问题，增强了系统的噪声鲁棒性。

为实现上述目的，本申请技术方案为：一种基于压缩感知与熵的多天线宽带频谱检测方法。首先，利用离散分数阶傅里叶变换(dfrft)算法对信号进行稀疏表示；然后，通过共享各阵元接收信号之间稀疏系数的先验信息，基于层次贝叶斯概率模型的多任务压缩感知技术，对稀疏系数进行重构，以得到原信号；最后，对其频域统计量，基于信息熵进行频谱判决。该方案的具体步骤为：

s1：建立接收信号模型；

s2：基于压缩感知的多天线宽带频谱感知算法重构得到原稀疏信号；

s3：基于信息熵进行频谱判决。

进一步地，建立接收信号模型具体是：假设空间中有w个分量组成的宽带chirp类干扰信号xw，入射至一个具有q阵元的均匀线性阵列，则第i个阵元接收信号以间隔δt进行采样，表示为：

yi(n)＝xwi(n)+ei(n),(i＝1,2,…,q)(1)

其中，yi(n)为阵元接收信号采样值，xwi(n)为干扰信号采样，ei(n)为噪声信号采样。

进一步地，对采样公式进行l点离散分数阶傅里叶变换，则各阵元接收信号的dfrft表示为：

yi(γ,m)＝zwi(γ,m)+ε,(i＝1,2,…,q)(2)

其中，γ∈[-π,π]为旋转角度，m为分数阶采样点数，zwi(γ,m)为干扰信号的dfrft，ε为噪声信号ei(n)的dfrft。

进一步地，基于压缩感知的多天线宽带频谱感知算法重构得到原稀疏信号，具体步骤是：

l次快拍下的接收信号表示为：

采样信号的dfrft表示为：

其中l为采样点数，表示相应信号是l维的，为实数值；

每一个阵元接收信号的重构过程均对应一个重构任务，多个阵元实现多任务重构；根据压缩感知理论，则第i个阵元接收信号的数学模型表示为：

gi＝φiyi＝φif(zi+εi)＝tizi+εi(5)

其中，φi为高斯观测矩阵；f为dfrft变换基；zi第i个阵元的dfrft稀疏向量；εi为第i个阵元均值为0，方差为β^-1的测量噪声向量；ti为第i个阵元全息观测矩阵。

进一步地，由观测数据向量gi，得到关于参数zi和β的似然函数，表示为：

其中，gi为第i个阵元的观测向量；mi为观测向量gi的纬度。

进一步地，为每个任务的稀疏向量zi都引入一个超参数向量α，鉴于q个任务相关，每个任务通过与所有任务共享超参数α，以得到各自的先验；考虑零均值的高斯先验，则zi的先验表示为：

其中，zij表示压缩感知任务i的第j个dfrft系数，αj对应zij的精度(方差的倒数)，α＝(α1,…,αl)^t。

进一步地，利用bayes法则，计算zi的后验概率，即：

均值和方差分别为：

μi＝βσiti^tgi(9)

σi＝(βti^tti+a)^-1(10)

由于矩阵a或者α中的参数是未知的；将重构zi转换为对参数α的估计问题；并通过确定非零元素的位置获得zi。

α和β的值通过最大化边缘似然函数得到，边缘似然函数通过对稀疏向量积分的形式得到，即：

通过计算求得对数边缘似然函数，即：

目标是关于超参数α和β的最大化，令对数边缘似然函数的导数为零，进一步得到超参数估计方程：

其中，μij为第i个后验均值μi的第j个分量，gij为第i个观测向量gi的第j个分量，τj＝1-αjσii度量对应的zi由观测数据确定的效果，σii为后验协方差σi的第i个对角元素，||·||2表示向量的l2范数。

进一步地，得到稀疏向量的估计值

更进一步地，基于信息熵进行频谱判决的具体步骤是：对重构的原信号作l点dft(对应于γ＝π/2的dfrft)，即：

其中，ε(m)分别为接收信号、干扰信号和噪声信号的频谱。

基于频域熵的信号检测建模为：

hj0vs.hj1(16)

利用直方图法来估计每个状态的概率，得到信号的信息熵与其对应的统计量，表示为：

在假设hk下，状态空间维度为j(概率空间维度)的随机变量r的信息熵为hjk(r)；根据r的取值个数(状态数)，将其分成j个单元格，每个单元格b的大小为：b＝(rmax-rmin)/j，ni则表示位于第i个单元格b内的频点数，总个数为因此，频率出现在第i个单元格的概率为pi＝ni/l；

由上述分析，基于熵的频谱判决算法，表示为：

等于0表示可用频段，否则为干扰频段，阈值λ定义为：

λ＝hj+q^-1(1-pfa)β^-1/2(19)

式中：hj为理论噪声熵，δ是euler-mascheroni常数，q^-1(·)是q函数的逆，β是h在h0下的噪声精度(方差的倒数)，由neyman-pearson准则，pfa是理论虚警概率。

进一步地，基于统计的检测概率和虚警概率分别定义为:

其中，lt为总共检测数，ld为正确检测数，lfa为虚警数。

基于以上分析，本文提出的csma-wsd算法，可具体描述为，如表1所示。

表1csma-wsd算法

本申请的有益效果：第一，采用多天线技术可提高单节点检测能力；第二，利用贝叶斯压缩感知方法，解决了测量不确定性，可提高信号重构精度；第三，采用基于熵的频域频谱判决方法，解决噪声不确定的问题，可增强系统噪声鲁棒性。针对普遍存在的宽带chirp类干扰信号的检测问题，本方法检测性能较好，一定程度上解决了对chirp类干扰分析检测困难的难题。

附图说明

图1为本发明实现的流程图。

图2为阵列接收信号的二维dfrft幅度谱图。

图3为阵列接收信号的三维dfrft幅度谱图。

图4为不同观测值下采用不同算法重构性能比较。

图5为不同观测数下重构误差比较。

图6为不同观测数下重构精度比较。

图7为不同snr下检测概率的(噪声不确定度±3db)。

具体实施方式

为了使本发明的目的、技术方案和优点更加清楚，下面结合附图和具体的实施方式对本发明进行详细描述。

本实施例提出一种基于压缩感知与熵的多天线宽带频谱检测方法，该方法的具体步骤为：

s1：建立接收信号模型

假设空间中有w个分量组成的宽带chirp类干扰信号xw入射至一个具有q阵元的均匀线性阵列，则第i个阵元接收信号以间隔δt的采样可表示为：

yi(n)＝xwi(n)+ei(n),(i＝1,2,…,q)(1)

其中，n＝0,1,…,l-1，ei(n)为噪声信号。

基于式(1)，利用ozaktas提出的分解型离散frft(dfrft)算法对其进行l点dfrft变换，则各阵元接收信号的dfrft可表示为：

yi(γ,m)＝zwi(γ,m)+ε,(i＝1,2,…,q)(2)

其中，γ∈[-π,π]为dfrft旋转角度，m为分数阶采样点数，zwi(γ,m)为多分量chirp干扰信号dfrft，ε为噪声信号dfrft。

s2：基于压缩感知的多天线宽带频谱感知算法重构得到原稀疏信号；

基于式(1)，l次快拍下的接收信号可表示为：

由式(2)采样后得到信号的dfrft可表示为：

每一个阵元接收信号的重构过程都对应一个重构任务，多个阵元可实现多任务重构。根据压缩感知理论，则第i个阵元接收信号的数学模型可表示为：

gi＝φiyi＝φif(zi+εi)＝tizi+εi(5)

其中，为q组mi×l维高斯观测阵，f为dfrft变换基，为的dfrft系数，考虑到由测量不确定引入的噪声，设是一均值为0，方差为β^-1的测量噪声向量，ti＝φif为全息观测矩阵，为q组mi×1维的观测向量。

由观测数据向量gi，得到关于参数zi和β的似然函数，可表示为：

基于此，为每个任务的稀疏向量zi都引入一个超参数向量α，鉴于q个任务相关，每个任务可通过与所有任务共享超参数α，以得到各自的先验。考虑零均值的高斯先验，因此zi的先验可表示为：

其中，zij表示压缩感知任务i的第j个dfrft系数，αj对应zij的精度(方差的倒数)，α＝(α1,…,αl)^t。

需要注意的是，超参数与zi的稀疏性直接相关，具体为:1)当αj很大时，zij的方差很小，因zij的均值为0，所以zij可当作0；2)当αj很小时，zij的方差很大，所以zij非零。

基于式(6)和式(7)，可利用bayes法则，计算zi的后验概率，即：

其中，均值和方差分别为：

μi＝βσiti^tgi(9)

σi＝(βti^tti+a)^-1(10)

其中，a＝diag(α1,α2,…,αl)。当μi和σi已知时，估计zi的方法有很多种，即可得到zi的估计，其可表示为

然而，矩阵a或者α中的参数是未知的。基于此，可将重构zi转换为对参数α的估计问题。并通过确定非零元素的位置获得zi。

α和β的值可通过最大化边缘似然函数得到，边缘似然函数通过对稀疏向量积分的形式得到，即：

式(11)表示两个高斯分布的卷积，因此通过计算求得对数边缘似然函数，即：

其中，ci＝β^-1i+tia^-1ti^t。

目标是关于超参数α和β的最大化式(12)，令对数边缘似然函数的导数为零，可进一步得到超参数估计方程，即：

其中，μij为第i个后验均值μi的第j个分量，gij为第i个观测向量gi的第j个分量，τi＝1-αjσii度量对应的zi由观测数据确定的效果，σii为后验协方差σi的第i个对角元素，||·||2表示向量的l2范数。

考虑每一个超参数均对应于一个稀疏向量，通过计算可得众多超参数α均趋于无穷大，其对于稀疏向量映射为观测向量是无效，即稀疏向量可自动得出。基于此，可得稀疏向量的估计值

s3：基于信息熵进行频谱判决

基于能量检测的频谱判决方法建模为二元假设检验，但由于统计量与信号功率相关，故其易受噪声不确定性影响，在低信噪比场景下，算法检测性能较差。针对上述问题，可采用基于熵的频域频谱判决(frequencydomainentropy，fde)算法。

考虑到实际的通信过程在频域实现，则对重构后的稀疏信号，可通过逆变换求出各阵元的原信号估计并对其作dft将其映射至频域，以进行最终的频谱判决。基于式(2)，对重构的原信号作l点dft(对应于γ＝π/2的dfrft)，即：

式中，ε(m)分别为接收信号、干扰信号和噪声信号的频谱。

考虑到信号谱的幅度值具有随机性，将其记为随机变量r，并通过估计其概率密度函数来表示被测量信号。基于此，基于频域熵的信号检测可建模为：

hj0vs.hj1(16)

其中，在假设hk下，状态空间维度为j(概率空间维度)的随机变量r的信息熵为hjk(r)。

为减少计算复杂度，利用直方图法来估计每个状态的概率。根据r的取值个数(状态数)，将其分成j个单元格，每个单元格b的大小为：b＝(rmax-rmin)/j，ni则表示位于第i个单元格b内的频点数，总个数为因此，频率出现在第i个单元格的概率为pi＝ni/l，则可得到信号的信息熵与其对应的统计量，可表示为：

由上述分析，基于熵的频谱判决算法，可表示为：

其中，等于0表示可用频段，否则为干扰频段，阈值λ定义为：

λ＝hj+q^-1(1-pfa)β^-1/2(19)

式(20)中hj为理论噪声熵，δ是euler-mascheroni常数，q^-1(·)是q函数的逆，β是h在h0下的噪声精度(方差的倒数)，由neyman-pearson准则，pfa是理论虚警概率。

基于统计的检测概率和虚警概率分别定义为:

其中，lt为总共检测数，ld为正确检测数，lfa为虚警数。

为模拟测量的不确定性，给每个观测数据向量加入均值为0，方差为δ＝1的高斯噪声。

为验证重构效果，将重构误差和精度定义为：

其中，z为原稀疏信号向量，为重构稀疏信号向量。

仿真内容：

本文通过matlab仿真进一步验证所提算法的有效性。需要说明的是，为表征阵元信号之间的相关信息，故将其量化为稀疏向量间的支撑集(幅值与位置)相似度。仿真环境为：intel(r)core(tm)i7-4790cpu@3.6ghz,16gbram,matlab2018a,dell。

仿真参数设置如下：1)阵元个数q＝3；2)多分量宽带chirp干扰信号分量个数w＝6；3)相对于基阵元，阵元2和3的相似度分别设为95％，80％；4)各阵元观测矩阵观测维数m分别设为60，50，40。

仿真1：多分量chirp信号，设置仿真参数：快拍数，l＝1024，信号脉冲宽度t＝16μs，信号采样频率fs＝64mhz，信噪比snr＝0db，各分量信号带宽[b1,b2,b3,b4,b5,b6]＝[50,55,60,65,70,75](mhz)，调频率[k1,k2,k3]＝[3.125,3.438,3.75](mhz/μs)，[k4,k5,k6]＝[4.063,4.375,4.688](mhz/μs)，由旋转角度γ＝arccot(-kl/fs²),得到：[γ1,γ2,γ3,γ4,γ5,γ6]＝[0.908,0.861,0.817,0.778,0.741,0.706](rad)。

检验信号dfrft稀疏表示效果。图2为含有多分量chirp信号的二维dfrft幅度谱图，图3为信号三维dfrft幅度谱图。

由图2与图3可知，在分数域的信号噪声值远小于chirp信号谱峰值，且仅在极少的位置，出现明显峰值，而多数位置为很小值，表现出良好的稀疏特性，则可利用压缩感知技术对信号进行后续处理。

仿真2：检验信号重构效果。图4为信号稀疏系数与其重构情况。图4(a)-(c)为三个阵元信号的dfrft，图4(d)-(f)、(g)-(i)和(j)-(l)分别为利用mp、单任务bcs和csma-wsd重构算法得到的重构结果。

由图4可知，a)相同观测数下，与贝叶斯算法相比，由于mp算法对测量不确定性敏感，则其重构效果较差；b)不同观测数下，随着观测数减少，单任务bcs算法重构效果变差，mp算法无法进行有效重构，csma-wsd算法则可获得较好重构效果，其归因于csma-wsd算法利用多天线接收信号的相关信息，故重构效果受观测数影响较小，具有较好的重构性能。

仿真3：考虑重构误差来定量分析重构效果，蒙特卡罗仿真循环次数为100。

图5为不同观测数下重构误差曲线仿真图。由图可知，信号相似度在95％，80％的多任务重构算法与单任务bcs重构算法、mp重构算法相比，由于共享阵元信号相关信息降低了对观测数据数量的严格要求，随着观测数的增加，较单任务bcs算法，多任务重构算法收敛更快，趋于稳定时需要的观测数更少。此外，图中误差棒给出了重构信号的置信度，用于描述测量的不确定性。

仿真4：考虑重构精度分析重构效果，蒙特卡罗仿真循环100次。

图6为信号重构正确率随观测数变化的仿真曲线。由图可知，多任务bcs算法对信号之间的相关信息依赖性较强，故在相同观测数下，相似度越大，信号重构精度越高。此外，多任务bcs算法在观测数为50后可趋于稳定，而单任务bcs和mp算法要达到同样的重构效果，则需要更多的观测数据，亦会带来更大的计算量。

仿真5：考虑信噪比变化对检测性能的影响，其中，噪声波动的不确定性通过改变信噪比体现。图7为噪声不确定度设为±3db，理论虚警概率pfa为0.01下，感知时间ts＝0.1ms，基于统计的检测概率关于信噪比snr的变化曲线仿真图。

由图7表明，在信噪比为snr＝-10db时，单节点的ed算法和fde算法无法进行有效检测，而协作式感知算法和多天线感知算法的检测概率均大于55％。与or-css算法相比，由于利用贝叶斯概率模型，csma-wsd算法和bcs-css算法检测效果较优，具有更好的测量不确定性和鲁棒性。此外，由于bcs-css方法需将多个节点数据发给融合中心进行融合，故其会占用额外的通信信道,亦会引入更多的噪声，而csma-wsd算法采用多天线技术，未利用远距离数据传输融合过程，并采用基于熵的频谱判决算法,故在低信噪比场景下，能够取得较好的检测性能。

仿真结果表明，在测量数据较少场景下，与匹配追踪和单任务贝叶斯算法相比，信号重构精度较高；且在低信噪比条件下，与已有算法相比，具有较好的检测性能。

由此，本发明所提算法针对普遍存在的宽带chirp类干扰信号的检测问题检测性能较好，一定程度上解决了对chirp类干扰分析检测困难的难题。因此，将本文算法应用于军用无人机等电子战设备，可有效对抗恶意线性调频雷达干扰，确保通信安全。

发明针对已有单节点频谱感知精度低、协作频谱感知数据融合过程复杂，以及对噪声不确定性敏感等问题，提出一种基于压缩感知与熵的多天线宽带频谱检测方法。该算法利用多天线技术，通过共享各阵元接收信号之间的相关信息，建立多任务学习模型，实现阵元之间的协作感知，进而提高单节点感知精度；基于贝叶斯概率模型，解决测量不确定性问题，可提高宽带信号重构精度；并利用频域信息熵进行频谱判决，能够改善算法的噪声鲁棒性。