可重构智能表面辅助的多用户MIMO上行链路传输方法与流程

本发明属于通信领域，具体涉及一种利用部分信道状态信息的可重构智能表面辅助的多用户mimo上行链路传输方法。

背景技术：

可重构智能表面(reconfigurableintelligentsurface，ris)是由电磁材料构成的可编程表面，由集成电子设备控制，是超材料的二维应用。ris配置若干个反射单元，可改变入射到其上信号的相位，而不改变入射信号的幅度。

在ris辅助的无线通信系统中，ris可以构建智能无线电环境，即可控、可重新配置的传播环境。进而，无线通信系统可以缓解由无线信道多径传播和多普勒扩展等引起的影响，从而提升系统性能。

在本发明考虑的ris辅助的多用户mimo上行链路传输过程中，各个用户端发送信号，信号经ris反射到基站。传统的无线通信传输优化问题常基于瞬时信道状态信息，但是对于ris辅助的无线通信系统，瞬时信道状态信息的获取较为困难，并且利用瞬时信道状态信息实施传输会增大ris的功率消耗。

技术实现要素：

发明目的：针对ris辅助的多用户mimo上行链路传输，本发明提供一种利用部分信道状态信息的ris辅助的多用户mimo上行链路传输方法，能够有效提高系统传输性能，降低实现复杂度，并提升传输鲁棒性。

技术方案：为实现上述发明目的，本发明所述的ris辅助的多用户mimo上行链路传输方法，包括以下步骤：

各个用户端发送信号，信号经可重构智能表面ris反射到达基站；所述ris对各用户端发送的信号进行相位的调整；各用户端信号的发送方向，即发送协方差矩阵的特征向量由各用户到ris的信道信息确定，各用户端的发送功率分配矩阵和ris相移矩阵根据系统全局能量效率最大化准则或者系统遍历频谱效率最大化准则进行联合设计；所述系统全局能量效率是系统遍历频谱效率与系统总消耗功率的比值，遍历频谱效率为各用户频谱效率的统计平均，利用ris到基站信道的瞬时信道状态信息和各用户到ris信道的统计信道状态信息；联合优化的目标为在同时满足各用户发送功率约束及ris各单元相移恒模约束下最大化系统全局能量效率或最大化系统遍历频谱效率；

其中各用户端的发送功率分配矩阵和ris相移矩阵的联合优化基于如下交替优化方法，包括：对于给定的ris相移矩阵，利用确定性等同原理和dinkelbach变换对各用户端进行系统全局能量效率最大化准则下的发送功率矩阵设计，或者利用确定性等同原理对各用户端进行遍历频谱效率最大化准则下的发送功率矩阵设计；对于给定的发送功率分配矩阵，采用块坐标下降法和minorization-maximization(mm)方法对ris相移矩阵进行设计；交替实施上述发送功率分配矩阵和ris相移矩阵的联合优化直至相邻两次全局能量效率值或者遍历频谱效率之差小于某个给定的阈值；

随着通信过程中各用户和ris之间的统计信道状态信息以及ris和基站之间的瞬时信道状态信息变化，用户端根据更新后各用户和ris之间的统计信道状态信息以及ris和基站之间的瞬时信道状态信息，动态实施ris辅助的多用户mimo上行链路传输方法。

作为优选，各用户端信号的发送方向，即发送协方差矩阵的特征向量由其到ris的信道统计协方差矩阵的发送端特征模式矩阵确定。

作为优选，所述对于给定的ris相移矩阵，利用确定性等同原理和dinkelbach变换对各用户端进行系统全局能量效率最大化准则下的发送功率矩阵设计，包括以下步骤：

(1)根据大维随机矩阵理论，计算系统遍历频谱效率的确定性等同值，进而计算全局能量效率的确定性等同值，以降低问题求解的复杂度；

(2)基于确定性等同计算结果，将问题目标函数转换为分子为关于功率分配矩阵的凹函数，分母为关于功率分配矩阵的线性函数的分式优化问题，基于dinkelbach变换，引入辅助变量将分式问题转化为一系列凸优化子问题，此辅助变量随着迭代过程不断更新；迭代过程在相邻两次迭代结果之差小于某个给定阈值时终止，此时得到的解为ris相移矩阵给定时系统全局能量效率最大化准则下各用户端发送功率矩阵的解。

作为优选，所述对于给定的发送功率分配矩阵，采用块坐标下降法和mm方法对ris相移矩阵进行设计，包括以下步骤：

(1)忽略优化问题中与相移矩阵无关的，可视为常数的项，引入两个辅助变量，将得到的非凸优化问题转化为等效的均方误差最小化问题；

(2)通过块坐标下降法迭代优化最小化问题中的三个变量，包括一个相移矩阵和两个引入的辅助变量；在每次迭代中，固定其中两个变量求解另一变量，并将新求解出的变量代入下一次迭代中，其中求解两辅助变量时利用拉格朗日函数的一阶最优性条件给出解的闭式表达，求解相移矩阵时使用mm方法；每次迭代后求解均方误差最小化问题的目标函数，迭代过程在相邻两次迭代目标函数之差小于某个给定阈值时终止，此时得到的解为发送功率矩阵给定时，能量效率最大化准则下相移矩阵的解。

作为优选，所述系统遍历频谱效率表示为：

其中，为ris到基站的信道矩阵，为第k个用户到ris的统计特征模式域信道矩阵，为第k个用户到ris的信道矩阵，u2,k和v2,k是确定性酉矩阵，φ为ris相移矩阵，k为小区中用户数，nk为第k个用户的天线数，m为基站天线数，nr为ris的反射单元数，λk为第k个用户的发送信号的发送功率矩阵，im表示一个m×m的单位矩阵，σ²表示噪声方差，log表示对数运算，det表示取矩阵的行列式运算，e{.}表示期望运算。

作为优选，所述全局能量效率最大化准则下的优化问题表示为：

|φn|＝1,n＝1,...,nr,

其中，ξk(＞1)为第k个用户处功率放大器的放大系数，pc,k为第k个用户处的静态电路功耗，pbs和nrps分别为基站和ris的静态硬件耗散功率，pmax,k为第k个用户的发送功率约束，tr{·}表示取矩阵迹的运算，θn是ris的第n个反射单元引入的相移，是虚数单位，|x|表示取向量x的模。

作为优选，所述系统遍历频谱效率最大化准则下的优化问题表示为：

|φn|＝1,n＝1,...,nr,

作为优选，所述全局能量效率确定性等同的计算方法包括：

(1)依据大维随机矩阵理论，通过用户到ris信道的统计信道状态信息以及ris到基站信道的瞬时信道状态信息，迭代计算目标函数分子的确定性等同辅助变量直至收敛；

(2)利用迭代得到的确定性等同辅助变量计算目标函数分子的确定性等同表达；

(3)将目标函数分子的确定性等同表达带入能量效率最大化的功率分配优化问题中，降低运算的复杂度。

作为优选，基于mm方法求解ris相移矩阵的内层迭代方法包括：

(1)在块坐标下降法中，将两个辅助变量看作常数求解ris相移矩阵时，目标函数是相移矩阵的非凸函数，利用mm方法迭代求解；

(2)在每次迭代中，将目标函数替换为其上界函数，给出转换后问题解的闭合表达式，利用此解更新下一次迭代的目标函数，并计算原目标函数的值，在相邻两次迭代目标函数之差小于某个给定阈值时终止，终止时的相移矩阵为两个辅助变量给定时，均方误差最小化问题的解。

有益效果：与现有技术相比，本发明具有如下优点：

1.在ris辅助的无线通信系统中，ris可以构建智能无线电环境，即可控、可重新配置的传播环境。进而，无线通信系统可以缓解由无线信道多径传播和多普勒扩展引起的影响，从而提升系统性能。

2.本发明所提方法仅利用部分信道状态信息，包括慢时变的ris到基站信道的瞬时信道状态信息，快时变的用户到ris信道的统计信道状态信息。降低了信道状态信息获取的复杂度和开销，提升了系统的传输鲁棒性。

3.本发明所提方法利用交替优化、确定性等同原理、mm方法、块坐标下降法等优化方法，联合设计用户的发送协方差矩阵和ris相移矩阵以最大化系统全局能量效率或系统遍历频谱效率。本方法具有较好的收敛性，能显著降低优化问题求解和物理层实现的复杂度。

附图说明

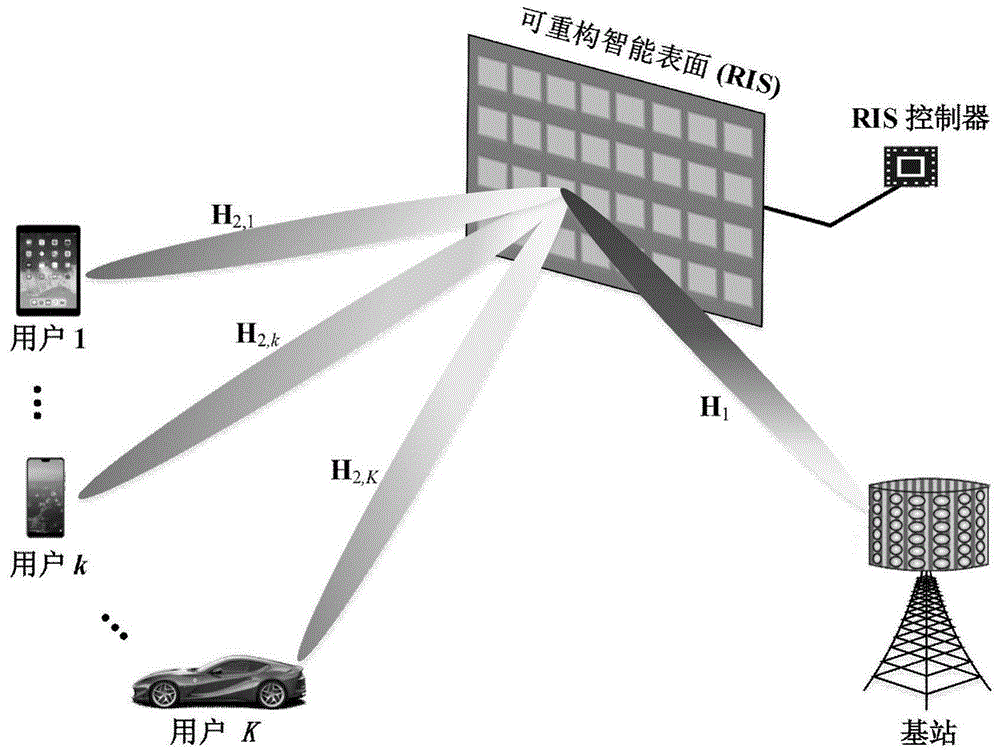
图1为本发明实施例的中ris辅助的多用户mimo上行通信示意图。

图2为本发明实施例的中基于dinkelbach变换的算法流程图。

图3为本发明实施例中基于确定性等同原理的迭代算法流程图。

图4为本发明实施例中的基于块坐标下降法和mm方法的算法流程图。

图5为本发明实施例中系统全局能量效率最大化准则下基于交替优化方法的算法流程图。

图6为本发明实施例中系统遍历频谱效率最大化准则下基于交替优化方法的算法流程图。

具体实施方式

为了使本技术领域的人员更好地理解本发明方案，下面将结合本发明实施例中的附图，对本发明实施例中的技术方案进行清楚、完整的描述，显然，所描述的实施例仅是本发明一部分实施例，而不是全部的实施例。基于本发明中的实施例，本领域普通技术人员在没有做出创造性劳动前提下所获得的所有其他实施例，都应当属于本发明保护的范围。

本发明实施例公开的可重构智能表面辅助的多用户mimo上行链路传输方法中，各个用户端发送信号，信号经ris反射到达基站。根据用户到ris和ris到基站的信道状态信息，各用户端发送信号，ris进行信号相位的调整。利用各用户到ris的信道统计协方差矩阵的发送端特征模式矩阵，确定各用户的发送协方差矩阵的特征向量，由此确定各用户信号的发送方向。系统进而实施全局能量效率最大化准则下或系统遍历频谱效率最大化准则下的各用户端功率分配矩阵和ris相移矩阵联合设计。随着通信系统中各用户移动等因素，用户和ris之间的统计信道状态信息以及ris到基站之间的瞬时信道状态信息变化，用户侧根据更新后的统计信道状态信息以及ris和基站之间的瞬时信道状态信息，重复前述步骤，进行ris辅助的多用户mimo上行链路传输方法，从而实现传输过程的动态更新，以保障传输性能。

实施功率分配矩阵和ris相移矩阵联合设计时，全局能量效率是遍历频谱效率与总消耗功率的比值；联合优化的目标为在满足各个用户端功率约束及ris各单元相移恒模约束下的情况下最大化系统全局能量效率或最大化系统遍历频谱效率；各用户端功率分配和ris相移矩阵联合优化基于交替优化方法、确定性等同原理、dinkelbach变换、块坐标下降法和mm方法等方法。

所述交替优化方法包括：对于给定的ris相移矩阵，利用确定性等同原理和dinkelbach变换对各用户端进行系统全局能量效率最大化准则下的发送功率矩阵设计，或者利用确定性等同原理对各用户端进行遍历频谱效率最大化准则下的发送功率矩阵设计；对于给定的发送功率分配矩阵，采用块坐标下降法和mm方法对ris相移矩阵进行设计；交替实施上述发送功率分配矩阵和ris相移矩阵的联合优化直至相邻两次全局能量效率值之差小于某个给定的阈值。

其中，对于给定的ris相移矩阵，利用确定性等同原理和dinkelbach变换对各用户端进行系统全局能量效率最大化准则下的发送功率矩阵设计，包括：

(1)根据大维随机矩阵理论，计算系统遍历频谱效率的确定性等同值，进而计算全局能量效率的确定性等同值，以降低问题求解的复杂度；

(2)基于确定性等同计算结果，将问题目标函数转换为分子为关于功率分配矩阵的凹函数，分母为关于功率分配矩阵的线性函数的分式优化问题，基于dinkelbach变换，引入辅助变量将分式问题转化为一系列凸优化子问题，此辅助变量随着迭代过程不断更新；迭代过程在相邻两次迭代结果之差小于某个给定阈值时终止，此时得到的解为ris相移矩阵给定时系统全局能量效率最大化准则下各用户端发送功率矩阵的解。

所述对于给定的发送功率分配矩阵，采用块坐标下降法和mm方法对ris相移矩阵进行设计，包括：

(1)忽略优化问题中与相移矩阵无关的，可视为常数的项，引入两个辅助变量，将得到的非凸优化问题转化为等效的均方误差最小化问题；

(2)通过块坐标下降法迭代优化最小化问题中的三个变量，包括一个相移矩阵和两个引入的辅助变量；在每次迭代中，固定其中两个变量求解另一变量，并将新求解出的变量代入下一次迭代中，其中求解两辅助变量时利用拉格朗日函数的一阶最优性条件给出解的闭式表达，求解相移矩阵时使用mm方法；每次迭代后求解均方误差最小化问题的目标函数，迭代过程在相邻两次迭代目标函数之差小于某个给定阈值时终止，此时得到的解为发送功率矩阵给定时，能量效率最大化准则下相移矩阵的解。

具体地，基于确定性等同的方法包括：

(a)依据大维随机矩阵理论，通过用户到ris信道的统计信道状态信息以及ris到基站信道的瞬时信道状态信息，迭代计算目标函数分子的确定性等同辅助变量直至收敛；

(b)利用迭代得到的确定性等同辅助变量计算目标函数分子的确定性等同表达；

(c)将目标函数分子的确定性等同表达带入能量效率最大化或者遍历频谱效率最大化的功率分配优化问题中，降低求期望运算的复杂度。

基于dinkelbach变换的迭代方法包括：

(a)能量效率最大化功率分配问题的目标函数是一个分式函数，其中分子是关于功率分配矩阵的凹函数，分母是关于功率分配矩阵的线性函数，即凹函数除以线性函数的分式优化问题；

(b)通过dinkelbach变换引入一个辅助变量将分式问题转化为一系列迭代求解的问题，其中每次迭代求解的子问题均为凸优化问题，辅助变量随着迭代过程不断更新；迭代过程在相邻两次迭代结果之差小于某个给定阈值时终止，此时的功率分配矩阵为相移矩阵给定时，能量效率最大化准则下的解。

基于块坐标下降法的外层迭代方法包括：

(a)经转化后的均方误差最小化问题有三个变量，包括一个相移矩阵和两个引入的辅助变量；

(b)使用块坐标下降法求解此问题，在每次迭代中，将其中两个变量看作常数，求解另一个变量；求解两辅助变量时利用拉格朗日函数的一阶最优性条件给出解的表达式，求解相移矩阵时使用mm方法；用更新后的变量值进行下一次迭代；

(c)每次迭代结束后，计算最小化问题目标函数的值，在相邻两次迭代目标函数的值之差小于某个给定阈值时终止，终止时的相移矩阵为发送功率矩阵给定时，全局能量效率最大化或者遍历频谱效率最大化准则下的解。

基于mm方法的内层迭代方法包括：

(a)在块坐标下降法中，将两个辅助变量看作常数求解相移矩阵时，目标函数是相移矩阵的非凸函数，利用mm方法迭代求解；

(b)在每次迭代中，将目标函数替换为其上界函数，给出转换后问题解的闭合表达式，利用此解更新下一次迭代的目标函数，并计算原目标函数的值，在相邻两次迭代目标函数之差小于某个给定阈值时终止，终止时的相移矩阵为两个辅助变量给定时，均方误差最小化问题的解。

下面结合具体场景对本发明实施例的具体步骤进行说明：

1)ris辅助的多用户mimo上行链路传播场景

考虑ris辅助的多用户mimo上行链路传播场景，基站配置m根天线，小区中有k个用户端，用户的集合为每个用户配置nk根天线。ris配置nr个反射单元，每个反射单元能够改变入射到其上的信号的相位，而不改变幅度。为ris相移矩阵，其中每个θn是ris的第n个反射单元引入的相移，是虚数单位。为ris到基站的信道矩阵，利用此信道的瞬时信道状态信息，为第k个用户到ris的信道矩阵，采用联合相关瑞利衰落信道模型，则h2,k可以表示为其中u2,k和v2,k是确定性酉矩阵，利用此信道的统计信道状态信息，即运算符⊙表示矩阵的hadamard乘积，e{.}表示期望运算，(.)^*表示矩阵的共轭运算。

系统的遍历频谱效率可以表示为：

其中，qk为第k个用户的发送信号的发送协方差矩阵，σ²表示噪声方差，log表示对数运算，det表示取矩阵的行列式，im表示一个m×m的单位矩阵，(.)^h表示矩阵的共轭转置运算。

系统的功耗模型为pk＝ξktr{qk}+pc,k+pbs+nrps，其中tr{·}表示取矩阵迹的运算，tr{qk}为第k个用户的发送信号功率，ξk(＞1)为第k个用户处功率放大器的放大系数，pc,k为第k个用户处的静态电路功耗，pbs和nrps分别为基站和ris的静态硬件耗散功率。

将系统的全局能量效率表示为遍历频谱效率与总消耗功率的比值，其中求期望运算是对各用户到ris的信道矩阵求期望：

则能量效率优化问题可以表示为：

其中pmax,k为第k个用户处发送功率约束，|φn|＝1确保了ris不改变入射到其上的信号的幅度。由于求解发送协方差矩阵复杂度很高，首先确定每个用户的最优传输方向，对发送协方差矩阵进行特征值分解，其中λk是第k个用户端的发送功率分配矩阵，vq,k是第k个用户端的发送信号方向矩阵。由于对于每一个用户，最优信号发射方向为各自用户端到ris信道发送协方差矩阵的特征向量，即由此可以将问题简化为：

问题进而变为能量效率最大化准则下的各用户端发送功率矩阵和ris相移矩阵联合设计。此问题目标函数为分式，期望运算复杂度很高，且需要联合优化多个目标矩阵。为此，本发明提出了一种利用部分信道状态信息的ris辅助的多用户mimo上行链路传输方法，该方法是基于交替优化、确定性等同原理、mm方法、dinkelbach变换和块坐标下降法的迭代优化算法。下面结合上述优化问题模型对涉及的各个算法做详细说明。

2)算法一：基于dinkelbach变换的算法

基于交替优化算法，首先考虑在相移矩阵φ给定时，根据系统全局能量效率最大化准则，求解各用户端发送功率矩阵的问题。问题表述如下：

定义其中n＝∑knk。则问题(5)中目标函数的分子可以写为

在计算目标函数表达式中的分子项，即系统频谱效率时，需要对信道进行遍历，计算期望值。由于该期望没有闭式表达式，因而需要monte-carlo仿真计算。为了降低求期望运算的复杂度，本发明利用大维矩阵随机理论计算目标函数的确定性等同表达。确定性等同方法利用用户到ris信道的统计信道状态信息以及ris到基站的瞬时信道状态信息，通过迭代计算确定性等同辅助变量，即可获得目标函数值的逼近结果。同时，确定性等同的结果可以很好逼近频谱效率项的准确表达，因此可以在基于dinkelbach变换的功率分配方法中利用确定性等同方法。图2示出了基于dinkelbach变换的算法流程图，算法的详细过程如下：

步骤1：给定一相移矩阵φ，初始化发送信号的功率分配矩阵λ⁽⁰⁾，设置迭代次数指示l＝0，阈值ε1；

步骤2：利用算法二，计算频谱效率r(λ)的确定性等同值

步骤3：将频谱效率替换为其确定性等同值，代入问题(5)中。根据dinkelbach变换原理，通过解决一系列凸优化子问题来求解问题(5)。其中第l次迭代时问题的形式为：

其中η是引入的辅助变量，通过以下等式迭代更新

求解此凸优化问题，得到本次迭代优化问题的解λ^(l+1)；

步骤4：将解出的λ^(l+1)代入式(7)中，计算新的辅助变量的值η^(l+1)。将此值与第l次迭代得到的结果η^(l)进行比较，如果两次的差|η^(l+1)-η^(l)|小于给定的阈值ε1，则终止迭代，步骤3中得到的功率分配矩阵λ^(l+1)作为给定相移矩阵时能量效率最大化准则下的解；否则，将迭代次数l加1，即l＝l+1，回到步骤2，将新的辅助变量的值代入，重新求解凸优化子问题，重复上述步骤。

当设计准则变为系统遍历频谱效率最大化时，只需将问题(5)目标函数的分母中的ξk,令为0。则问题变为关于功率分配矩阵的简单的非分式凸优化问题，如下所示：

只需求解一次凸优化问题(8)即可求出功率分配矩阵，而无需使用dinkelbach算法。

3)算法二：基于确定性等同原理的算法

为了计算目标函数的确定性等同值，首先对于每一个用户端引入确定性等同辅助变量，其中第k个用户的辅助变量为

其中γk和ψk分别是矩阵γ和ψ第k行的转置，矩阵和由下式确定：

其中是的第m列，λk,n,n和gk,n,n分别是λk和γk的第(n,n)个元素。

对于每一个用户，分别计算其确定性等同辅助变量，图3示出了基于确定性等同原理的算法流程图，算法的详细过程如下：

步骤1：初始化辅助变量设置迭代次数指示u＝0，阈值ε2；

步骤2：利用根据式(11)计算得到则

步骤3：利用根据式(12)计算得到则

步骤4：将第u+1次迭代得到的辅助变量的值与第u次迭代得到的结果进行比较，如果两次的差小于给定的阈值ε2，则终止迭代，转到步骤5；否则，将迭代次数u加1，即u＝u+1，回到步骤2，将本次迭代的解代入，重复上述步骤。

步骤5：将代入式(9)和(10)中，求得辅助变量的值γk和πk，则系统频谱效率的确定性等同值可表示为

4)算法三：基于块坐标下降法和mm方法的算法

基于交替优化算法，其次考虑给定发送功率矩阵λ＝diag{λ1,λ2,…,λk}时，求解相移矩阵φ的问题。问题表述为：

其中πk由确定性等同算法的公式(10)给出。问题(14)的目标函数中只有分子的第二项与φ相关，其余项可看作关于φ的常数，因此在优化时可以忽略常数项，将问题化简为

问题(15)的目标函数是非凸的，求解的复杂度高。首先将其转换为等效的均方误差最小化问题，问题表述如下：

其中，wc,uc是引入的辅助优化变量，

对于需要求解的三个变量wc,uc,φ，当其余两个变量固定时，目标函数是另一个变量的凹函数。因此可基于块坐标下降法，交替优化求解。当优化其中一个变量时，将另外两个变量看作常数。求解变量φ时用到了mm算法。图4示出了基于块坐标下降法和mm方法的算法实现过程，包括两层迭代，外层基于块坐标下降法的迭代过程如下：

步骤1：初始化wc⁽⁰⁾,uc⁽⁰⁾,φ⁽⁰⁾，设置外层块坐标下降法迭代次数指示s＝0，阈值ε3。计算问题(16)中的目标函数值h(wc^(s),uc^(s),φ^(s))；

步骤2：将uc^(s),φ^(s)看作常数，更新wc。利用目标函数h(wc,uc,φ)对wc的拉格朗日函数的一阶最优性条件可以得出wc的闭合表达式：

其中ec的值由将uc^(s),φ^(s)代入式(17)得到；

步骤3：将wc^(s+1),φ^(s)看作常数，更新uc。利用目标函数h(wc,uc,φ)对uc的拉格朗日函数的一阶最优性条件可以得出uc的闭合表达式：

步骤4：将wc^(s+1),uc^(s+1)看作常数，优化φ。由于定义利用内层基于mm算法的迭代算法求出解φ^(s+1)，则φ^(s+1)＝diag{φ^(s+1)}；

步骤5：根据更新后的参数计算目标函数值h(wc^(s+1),uc^(s+1),φ^(s+1))，将第s+1次迭代得到的目标函数的值与第s次迭代得到的结果进行比较，如果两次的差|h(wc^(s+1),uc^(s+1),φ^(s+1))-h(wc^(s),uc^(s),φ^(s))|小于给定的阈值ε3，则终止迭代，将步骤4中得到的相移矩阵的值作为给定功率分配矩阵时，ris相移矩阵的解；否则，将迭代次数s加1，即s＝s+1，回到步骤2，将本次迭代的解代入，重复上述步骤。

内层基于mm算法的迭代过程如下：

步骤1：在wc,uc都给定的情况下，将优化问题(16)重写为：

其中

由于定义分别为φ和c的对角元素组成的向量。则问题(21)可等效转换为

其中表示复数的实部。

步骤2：给定初值φ⁽⁰⁾，设置内层迭代次数指示i＝0，阈值ε4。计算问题(22)中的目标函数值g(φ⁽ⁱ⁾)；

步骤3：利用mm算法将问题(22)转化为一系列的凸优化子问题迭代求解。在第i次迭代时，将问题(22)的目标函数替换为其上界函数

其中φ⁽ⁱ⁾为第i-1次迭代时问题的解，λmax是矩阵s特征值的最大值。则第i次迭代的凸优化子问题为：

步骤4：计算α⁽ⁱ⁾的第n列向量为则可以写出子问题(24)的解为

步骤5：将第i+1次迭代得到的目标函数的值g(φ⁽ⁱ⁺¹⁾)与第i次迭代得到的结果g(φ⁽ⁱ⁾)进行比较，如果两次的差|g(φ⁽ⁱ⁺¹⁾)-g(φ⁽ⁱ⁾)|小于给定的阈值ε4，则终止迭代，步骤4中得到的φ⁽ⁱ⁺¹⁾为两辅助变量给定时，相移矩阵的解的对角线元素组成的矩阵；否则，将迭代次数i加1，即i＝i+1，回到步骤3，将本次迭代的解代入，重新计算凸优化子问题的解，重复上述步骤。

5)算法四：基于交替优化算法的全局能量效率最大化算法

基于交替优化方法原理，交替优化需要求解的两个变量，直到目标函数收敛。图5示出了基于交替优化方法的算法流程图，算法的详细过程如下：

步骤1：选取合适的初值λ⁽⁰⁾,φ⁽⁰⁾，设置迭代次数指示t＝0，阈值ε5；

步骤2：将λ^(t),φ^(t)代入算法二，计算确定性等同变量的表达式；

步骤3：将φ^(t)作为初值代入算法一：基于dinkelbach变换求解发送功率矩阵的算法中，解得发送功率矩阵λ^(t+1)；

步骤4：将λ^(t+1)和φ^(t)代入算法三：基于块坐标下降法和mm算法求解传输ris相移矩阵的算法中，解得相移矩阵φ^(t+1)；

步骤5：令根据式(2)计算目标函数，将第t+1次迭代结果gee(q^(t+1),φ^(t+1))与第t次迭代得到的结果gee(q^(t),φ^(t))进行比较，如果两次的差|gee(q^(t+1),φ^(t+1))-gee(q^(t),φ^(t))|小于给定阈值ε5，则终止迭代，得到能量效率最大化准则下发送功率矩阵和ris相移矩阵的解；否则，将迭代次数t加1，即t＝t+1，回到步骤2，将新的变量的值代入，重复上述步骤。

对于设计准则为系统遍历频谱效率最大化的交替优化算法，如图6，与上述过程类似，在步骤3中求解发送功率矩阵的问题是简单的非分式凸优化问题，不需要基于dinkelbach变换求解，直接求解优化问题(8)即解得发送功率矩阵λ^(t+1)。

随着通信系统中各用户到ris信道的统计信道状态信息以及ris到基站信道的瞬时信道状态信息变化，用户端根据更新后的统计信道状态信息以及ris和基站之间的瞬时信道状态信息，重复前述步骤，进行能量效率最大化或者遍历频谱效率最大化准则下的ris辅助的多用户mimo上行链路传输，从而实现传输过程的动态更新，以保障传输性能。